การวิเคราะห์ความแปรปรวนแบบสองทาง: คำจำกัดความ สูตร และตัวอย่าง

การวิเคราะห์ความแปรปรวนแบบสองทาง (“การวิเคราะห์ความแปรปรวน”) ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระตั้งแต่ 3 กลุ่มขึ้นไปที่กำหนดให้กับตัวแปรสองตัวหรือไม่ (บางครั้งเรียกว่า “ปัจจัย”)

บทช่วยสอนนี้จะอธิบายสิ่งต่อไปนี้:

• เมื่อใดจึงควรใช้การวิเคราะห์ความแปรปรวนแบบสองทาง
• สมมติฐานที่ต้องปฏิบัติตามเพื่อทำการวิเคราะห์ความแปรปรวนแบบสองทาง
• ตัวอย่างวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบสองทาง

เมื่อใดจึงควรใช้การวิเคราะห์ความแปรปรวนแบบสองทาง

คุณควรใช้การวิเคราะห์ความแปรปรวนแบบสองทางเมื่อคุณต้องการทราบว่าปัจจัย 2 ประการส่งผลต่อตัวแปรการตอบสนองอย่างไร และจะมีผลกระทบต่อการโต้ตอบระหว่างปัจจัยทั้งสองกับตัวแปรตอบสนองหรือไม่

ตัวอย่างเช่น สมมติว่านักพฤกษศาสตร์ต้องการสำรวจว่าแสงแดดและความถี่ในการรดน้ำส่งผลต่อการเจริญเติบโตของพืชอย่างไร เธอปลูกเมล็ดพืช 40 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาสองเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปสองเดือน เธอก็บันทึกความสูงของต้นไม้แต่ละต้น

ในกรณีนี้เรามีตัวแปรดังต่อไปนี้:

• ตัวแปรตอบสนอง: การเจริญเติบโตของพืช
• ปัจจัย: แสงแดด, ความถี่ในการรดน้ำ

และเราอยากจะตอบคำถามต่อไปนี้:

• แสงแดดส่งผลต่อการเจริญเติบโตของพืชหรือไม่?
• ความถี่ในการรดน้ำส่งผลต่อการเจริญเติบโตของพืชหรือไม่?
• มีผลกระทบต่อปฏิสัมพันธ์ระหว่างแสงแดดและความถี่ในการรดน้ำหรือไม่? (เช่น ผลของแสงแดดต่อพืชขึ้นอยู่กับความถี่ในการรดน้ำ)

เราจะใช้การวิเคราะห์ความแปรปรวนแบบสองทางสำหรับการวิเคราะห์นี้เนื่องจากเรามีปัจจัย สอง ประการ ในทางกลับกัน หากเราต้องการทราบว่าความถี่ในการรดน้ำเท่านั้นที่ส่งผลต่อการเจริญเติบโตของพืช เราจะใช้ การวิเคราะห์ความแปรปรวนแบบทางเดียว เนื่องจากเราจะทำงานกับปัจจัยเดียวเท่านั้น

สมมติฐานของการวิเคราะห์ความแปรปรวนแบบสองทาง

เพื่อให้ผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบสองทางถูกต้อง ต้องเป็นไปตามสมมติฐานต่อไปนี้:

1. ความปกติ – ตัวแปรการตอบสนองจะมีการกระจายตามปกติโดยประมาณสำหรับแต่ละกลุ่ม

2. ความแปรผันที่เท่ากัน – ความแปรปรวนสำหรับแต่ละกลุ่มควรจะเท่ากันโดยประมาณ

3. ความเป็นอิสระ – การสังเกตภายในแต่ละกลุ่มมีความเป็นอิสระจากกันและการสังเกตภายในกลุ่มได้โดยการสุ่มตัวอย่าง

การวิเคราะห์ความแปรปรวนแบบสองทาง: ตัวอย่าง

นักพฤกษศาสตร์ต้องการทราบว่าการเจริญเติบโตของพืชได้รับอิทธิพลจากการสัมผัสกับแสงแดดและความถี่ในการรดน้ำหรือไม่ เธอปลูกเมล็ดพืช 40 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาสองเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปสองเดือน เธอก็บันทึกความสูงของต้นไม้แต่ละต้น ผลลัพธ์แสดงไว้ด้านล่าง:

ในตารางด้านบน เราจะเห็นว่ามีการปลูกพืช 5 ต้นในแต่ละสภาวะรวมกัน

ตัวอย่างเช่น ปลูกต้นไม้ 5 ต้นโดยรดน้ำทุกวันและไม่มีแสงแดด และความสูงหลังจากสองเดือนคือ 4.8 นิ้ว 4.4 นิ้ว 3.2 นิ้ว 3.9 นิ้ว และ 4.4 นิ้ว:

เธอดำเนินการวิเคราะห์ ความแปรปรวนแบบสองทางใน Excel และได้รับผลลัพธ์ต่อไปนี้:

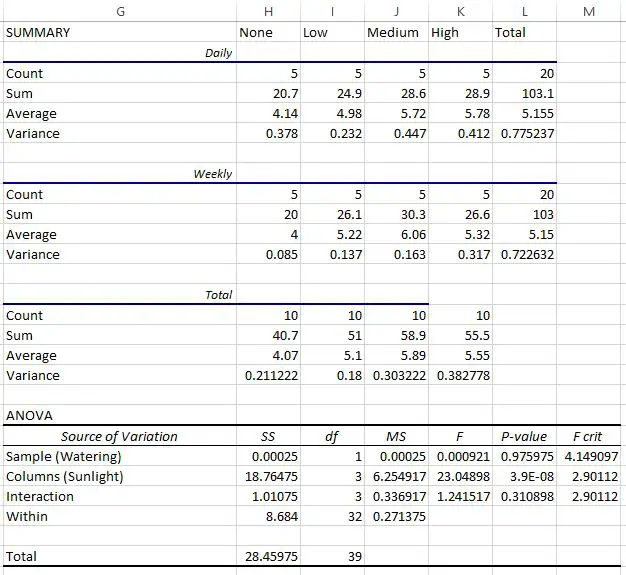
ตารางสุดท้ายแสดงผลของการวิเคราะห์ความแปรปรวนแบบสองทาง เราสามารถสังเกตได้ดังต่อไปนี้:

• ค่า p ของปฏิสัมพันธ์ระหว่างความถี่ในการรดน้ำและแสงแดดเท่ากับ 0.310898 ซึ่งไม่มีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05
• ค่า p ความถี่ในการรดน้ำเท่ากับ 0.975975 ซึ่งไม่มีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05
• ค่า p ของการรับแสงแดดคือ 3.9E-8 (0.000000039) ซึ่งมีนัยสำคัญทางสถิติที่ระดับอัลฟา 0.05

ผลลัพธ์เหล่านี้บ่งชี้ว่าแสงแดดเป็นปัจจัยเดียวที่มีผลกระทบที่มีนัยสำคัญทางสถิติต่อความสูงของพืช

และเนื่องจากไม่มีผลกระทบจากปฏิกิริยาใดๆ ผลของแสงแดดจึงสม่ำเสมอในแต่ละระดับของความถี่ในการรดน้ำ

พูดง่ายๆ ก็คือ ไม่ว่าต้นไม้จะรดน้ำทุกวันหรือทุกสัปดาห์ก็ไม่มีผลกระทบต่อแสงแดดที่ส่งผลต่อต้นไม้

แหล่งข้อมูลเพิ่มเติม

บทความต่อไปนี้จะอธิบายวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางโดยใช้ซอฟต์แวร์ทางสถิติที่แตกต่างกัน:

วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน Excel
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน R
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน Python
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน SPSS
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน Stata