การทดสอบความพอดีของไคสแควร์บนเครื่องคิดเลข ti-84

การทดสอบความดีพอดีของไคสแควร์ ใช้เพื่อพิจารณาว่าตัวแปรเชิงหมวดหมู่เป็นไปตามการแจกแจงเชิงสมมุติหรือไม่

บทช่วยสอนนี้จะอธิบายวิธีการทดสอบไคสแควร์พอดีบนเครื่องคิดเลข TI-84

ตัวอย่าง: การทดสอบความพอดีของไคสแควร์บนเครื่องคิดเลข TI-84

เจ้าของร้านบอกว่ามีลูกค้ามาที่ร้านในจำนวนเท่ากันทุกวันในสัปดาห์ เพื่อทดสอบสมมติฐานนี้ นักวิจัยอิสระจะบันทึกจำนวนลูกค้าที่เข้าร้านในสัปดาห์ที่กำหนดและพบสิ่งต่อไปนี้:

• วันจันทร์: ลูกค้า 50 คน
• วันอังคาร: ลูกค้า 60 คน
• วันพุธ: ลูกค้า 40 คน
• พฤหัสบดี: ลูกค้า 47 คน
• วันศุกร์: ลูกค้า 53 คน

เราจะใช้ขั้นตอนต่อไปนี้เพื่อทำการทดสอบความพอดีของไคสแควร์เพื่อตรวจสอบว่าข้อมูลสอดคล้องกับคำกล่าวอ้างของเจ้าของร้านค้าหรือไม่

ขั้นตอนที่ 1: ป้อนข้อมูล

ขั้นแรกเราจะใส่ค่าข้อมูลสำหรับจำนวนลูกค้าที่คาดหวังในแต่ละวันและจำนวนลูกค้าที่สังเกตในแต่ละวัน กด Stat จากนั้นกด EDIT ป้อนค่าต่อไปนี้สำหรับจำนวนลูกค้าที่สังเกตได้ในคอลัมน์ L1 และค่าสำหรับจำนวนลูกค้าที่คาดหวังในคอลัมน์ L2:

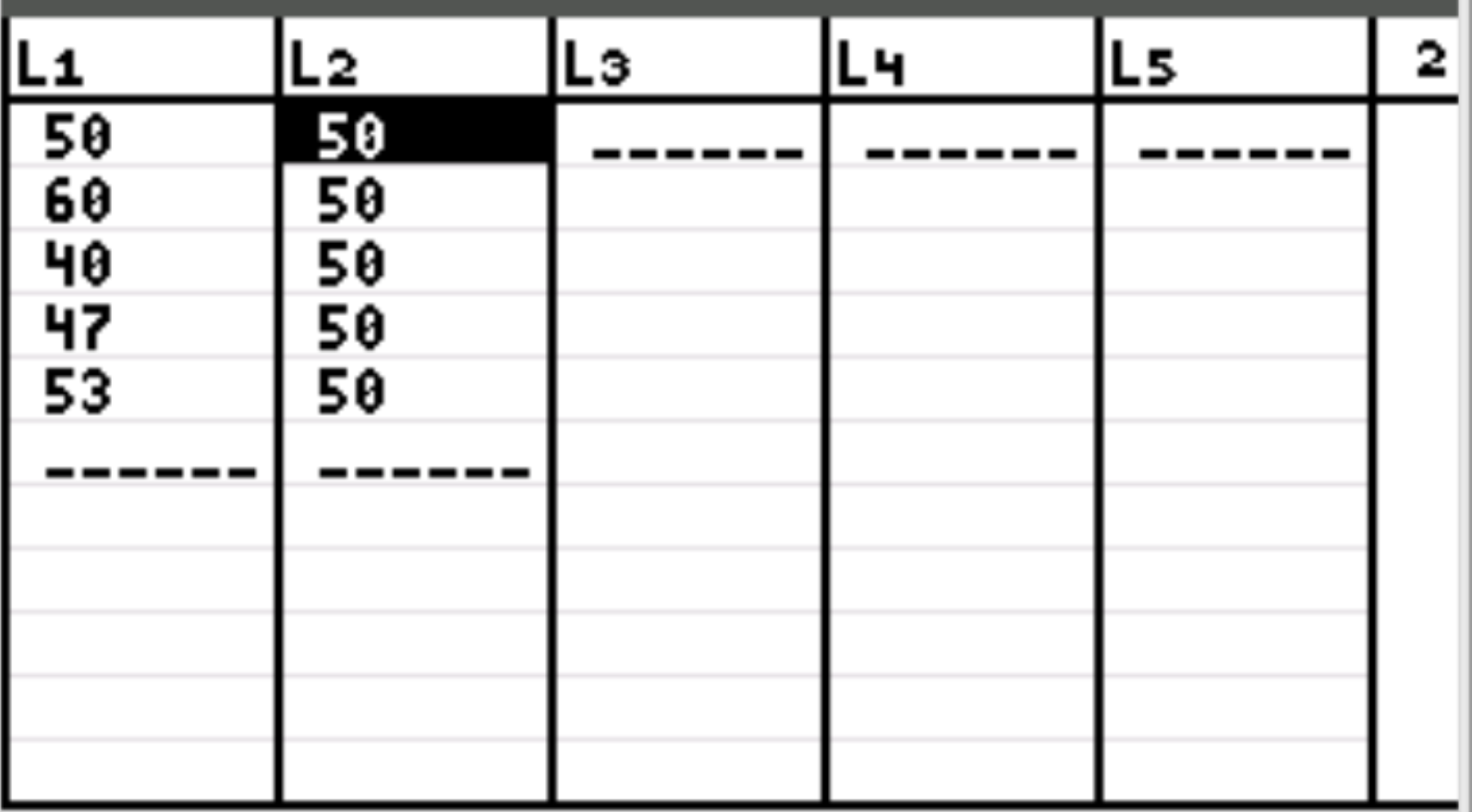
หมายเหตุ: มีลูกค้าทั้งหมด 250 ราย ดังนั้น หากเจ้าของร้านคาดหวังว่าลูกค้าเข้าร้านในจำนวนเท่ากันในแต่ละวัน ก็จะเท่ากับลูกค้า 50 รายต่อวัน

ขั้นตอนที่ 2: ทำการทดสอบความพอดีของไคสแควร์

ต่อไป เราจะทำการทดสอบความพอดีของไคสแควร์ กด Stat จากนั้นเลื่อนไปที่ TESTS จากนั้นเลื่อนลงไปที่ X ² GOF-Test แล้วกด Enter

สำหรับ Observed ให้เลือกรายการ L1 สำหรับ Expected ให้เลือกรายการ L2 สำหรับ df (องศาอิสระ) ให้ป้อน #categories – 1 ในกรณีของเรา เรามี 5-1 = 4 จากนั้นไฮไลต์ คำนวณ แล้วกด Enter

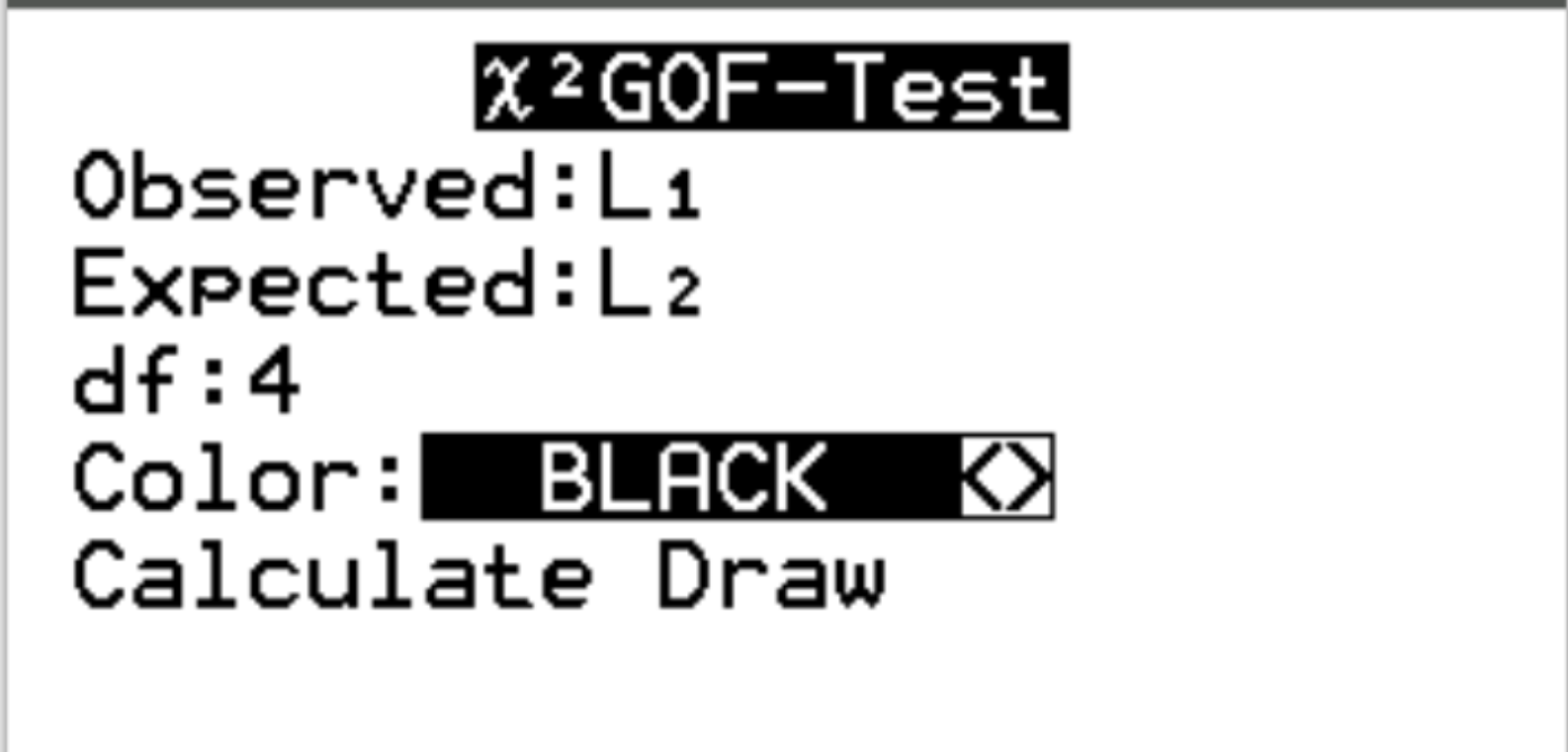
ผลลัพธ์ต่อไปนี้จะปรากฏขึ้นโดยอัตโนมัติ:

ขั้นตอนที่ 3: ตีความผลลัพธ์

สถิติการทดสอบ ^X2 สำหรับการทดสอบคือ 4.36 และค่า p ที่สอดคล้องกันคือ 0.3595 เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะบอกว่าการกระจายตัวของลูกค้าที่แท้จริงนั้นแตกต่างจากที่เจ้าของร้านค้ารายงาน