วิธีการคำนวณคะแนน z บนเครื่องคิดเลข ti-84
คะแนน z บอกเราว่าค่าที่กำหนดมาจากค่าเฉลี่ยเป็นจำนวนเท่าใด คะแนน z ของค่าที่กำหนดจะถูกคำนวณดังนี้:
คะแนน z = (x – μ) / σ
ทอง:
- x: ค่าส่วนบุคคล
- μ: ค่าเฉลี่ยประชากร
- σ: ส่วนเบี่ยงเบนมาตรฐานประชากร
บทช่วยสอนนี้จะอธิบายวิธีคำนวณคะแนน z บนเครื่องคิดเลข TI-84
วิธีคำนวณคะแนน Z ของค่าเดียว
สมมติว่าการแจกแจงปกติมีค่าเฉลี่ย 12 และส่วนเบี่ยงเบนมาตรฐาน 1.4 และเราต้องการคำนวณคะแนน z ของแต่ละค่า x = 14 ในการคำนวณคะแนน z ในเครื่องคิดเลข TI-84 เราเพียงแต่ พิมพ์สูตรต่อไปนี้:

สิ่งนี้บอกเราว่าค่าแต่ละตัว 14 มีคะแนน z เท่ากับ 1.4286 กล่าวอีกนัยหนึ่ง ค่า 14 คือ 1.4286 ส่วนเบี่ยงเบนมาตรฐานที่อยู่เหนือค่าเฉลี่ย
วิธีการคำนวณคะแนน Z ของหลายค่า
สมมติว่าเรามีรายการค่าข้อมูลและเราต้องการคำนวณคะแนน z สำหรับแต่ละค่าในรายการแทน ในกรณีนี้เราสามารถดำเนินการตามขั้นตอนต่อไปนี้:
ขั้นตอนที่ 1: ป้อนข้อมูล
ขั้นแรกเราจะใส่ค่าข้อมูล กด Stat จากนั้นกด EDIT ป้อนค่าต่อไปนี้ในคอลัมน์ L1:
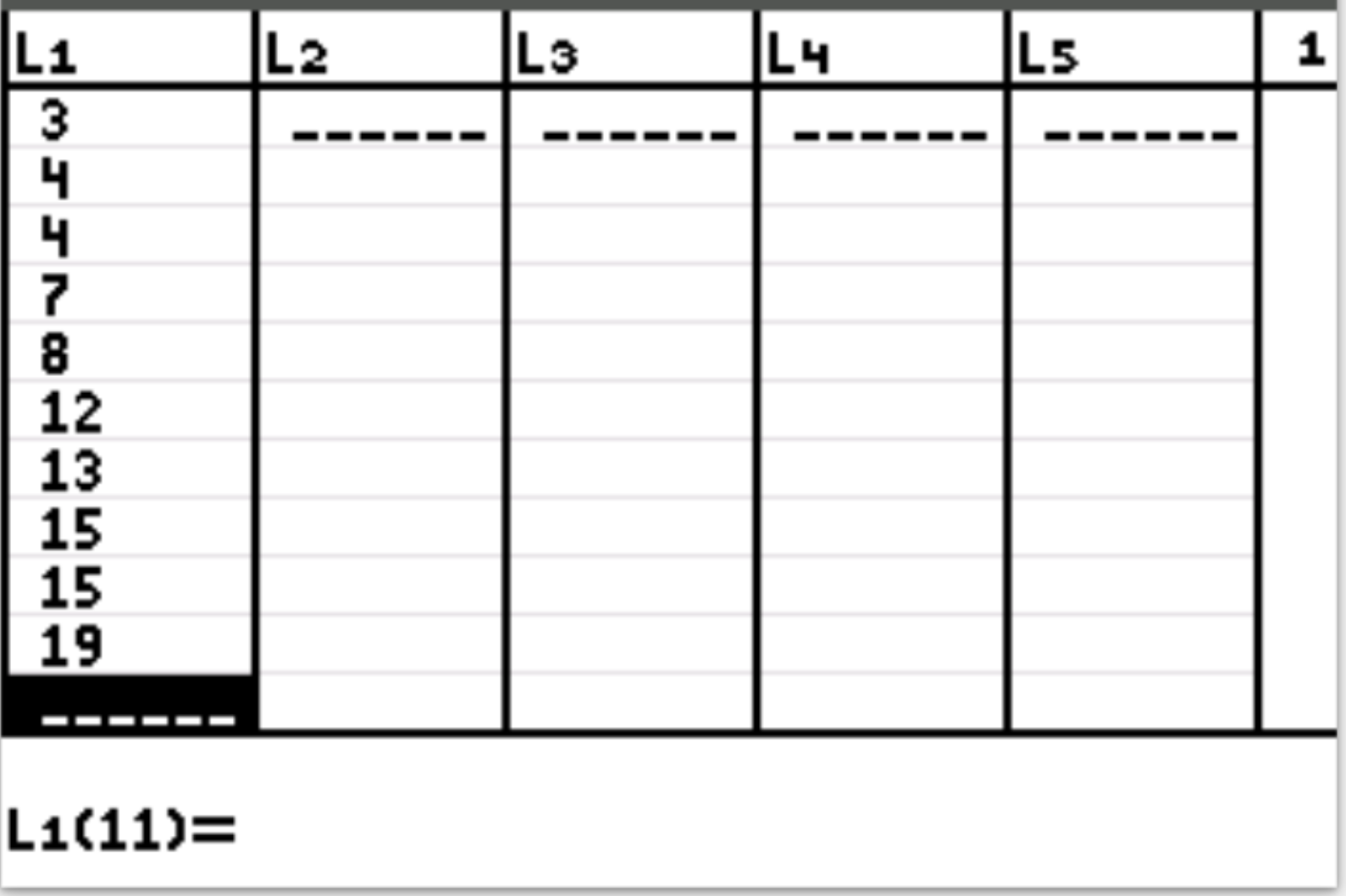
ขั้นตอนที่ 2: ค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของค่าข้อมูล
ต่อไป เราจะหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของชุดข้อมูล กด Stat จากนั้นเลื่อนไปที่ CALC ไฮไลต์ สถิติ 1-Var แล้วกด Enter
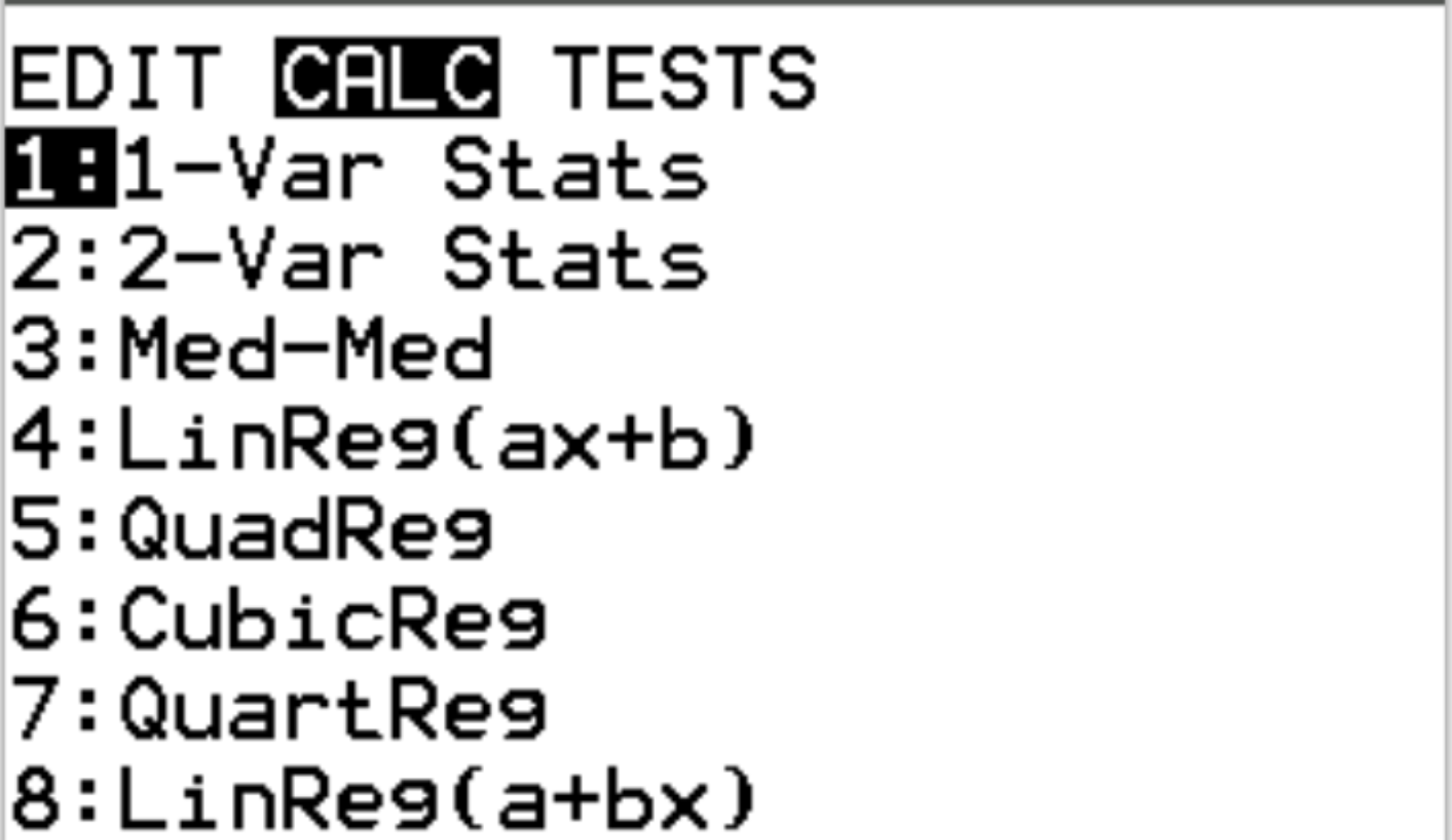
สำหรับ List ตรวจสอบ ให้แน่ใจว่าได้เลือก L1 เนื่องจากนี่คือคอลัมน์ที่เราป้อนข้อมูลลงไป ปล่อย FreqList ว่างไว้ ไฮไลต์ คำนวณ แล้วกด Enter

ผลลัพธ์ต่อไปนี้จะปรากฏขึ้น:
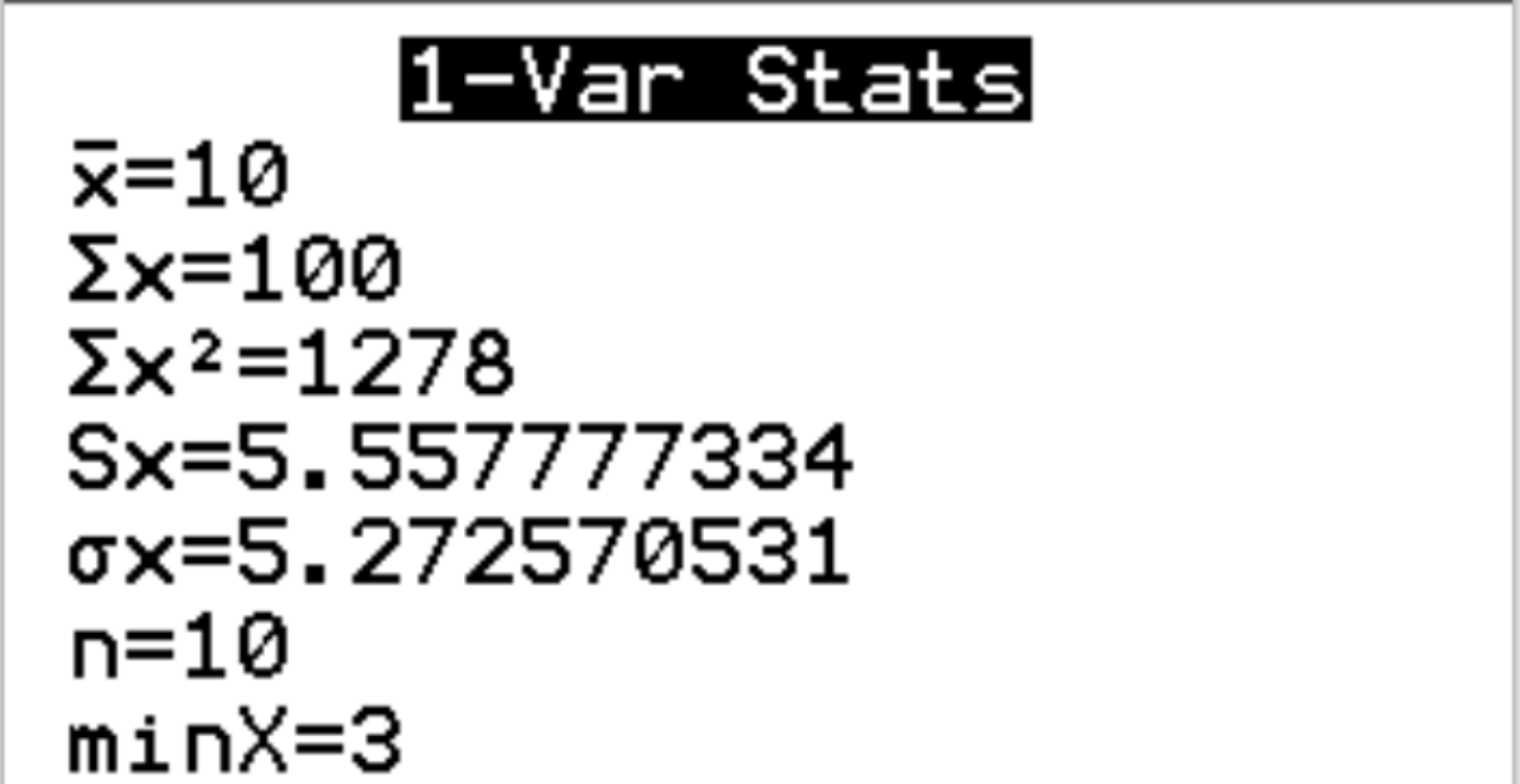
เราจะเห็นว่าค่าเฉลี่ยของชุดข้อมูลคือ x = 10 และค่าเบี่ยงเบนมาตรฐานคือ s x = 5.558 เราจะใช้ค่าทั้งสองนี้ในขั้นตอนถัดไปเพื่อคำนวณคะแนน z
ขั้นตอนที่ 3: ใช้สูตรเพื่อคำนวณคะแนน z แต่ละคะแนน
ต่อไป เราจะคำนวณคะแนน z สำหรับแต่ละค่าในชุดข้อมูล กด Stat จากนั้นกด EDIT ไฮไลต์ L2 แล้วพิมพ์สูตร ( L1-10)/5.558 จากนั้นกด Enter คะแนน z ของแต่ละค่าจะปรากฏในคอลัมน์ L2 โดยอัตโนมัติ:
หมายเหตุ: หากต้องการป้อน “L1” ลงในสูตร ให้กด 2 จากนั้นกด 1
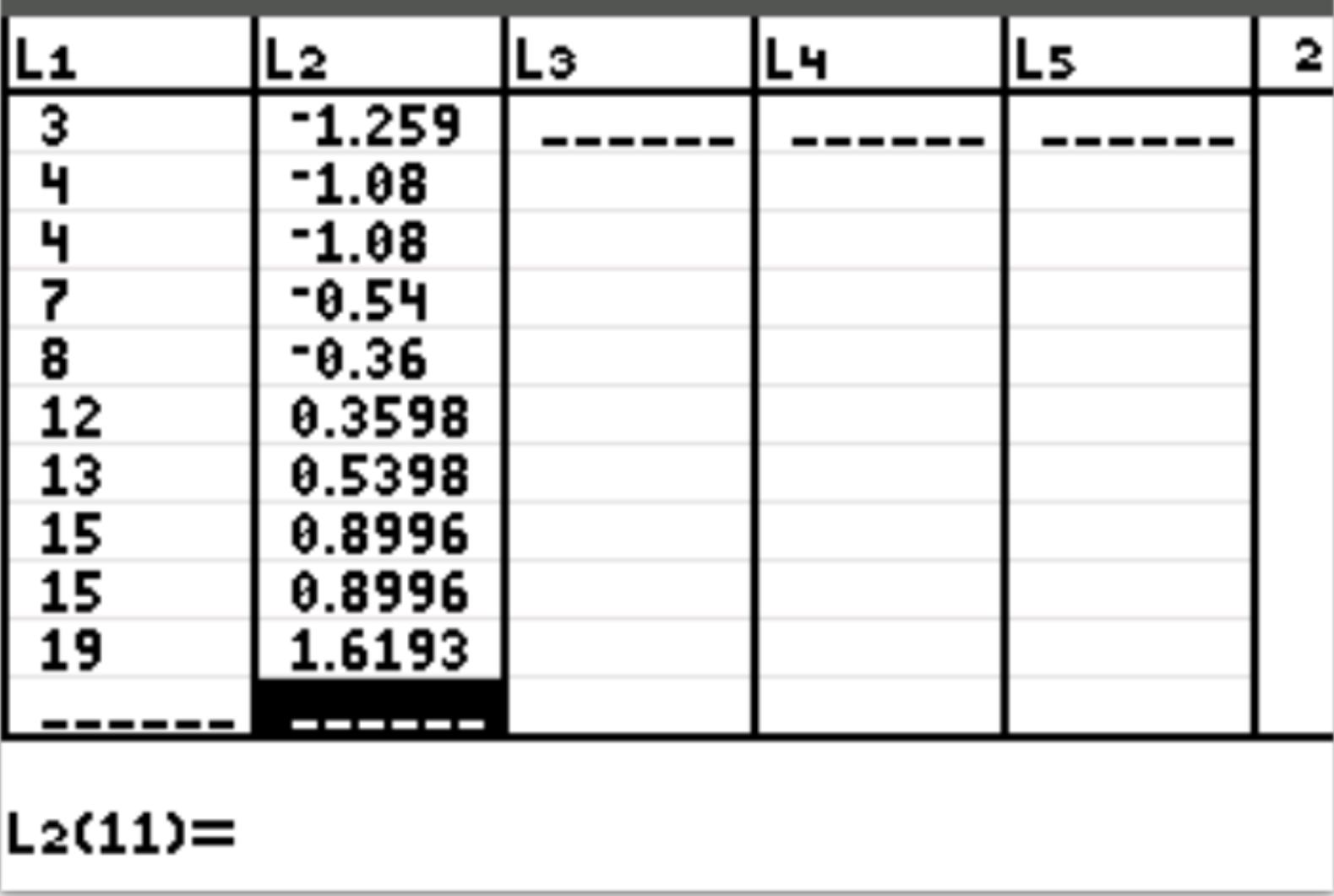
วิธีการตีความคะแนน Z
โปรดจำไว้ว่าคะแนน z เพียงบอกเราว่าค่าหนึ่งๆ มาจากค่าเฉลี่ยเป็นจำนวนเท่าใด คะแนน z อาจเป็นค่าบวก ลบ หรือเท่ากับศูนย์:
- คะแนน z ที่เป็นบวกบ่ง ชี้ว่าค่าใดค่าหนึ่งสูงกว่าค่าเฉลี่ย
- คะแนน z ติดลบบ่ง ชี้ว่าค่าใดค่าหนึ่งต่ำกว่าค่าเฉลี่ย
- คะแนน z ที่เป็นศูนย์บ่ง ชี้ว่าค่าใดค่าหนึ่งเท่ากับค่าเฉลี่ย
ในตัวอย่างของเรา เราพบว่าค่าเฉลี่ยคือ 10 และส่วนเบี่ยงเบนมาตรฐานคือ 5.558
ดังนั้นค่าแรกในชุดข้อมูลของเราคือ 3 ซึ่งมีคะแนน z (3-10)/5.558 = -1.259 ซึ่งหมายความว่าค่า “3” คือค่าเบี่ยงเบนมาตรฐาน 1.259 ซึ่ง ต่ำกว่า ค่าเฉลี่ย

ค่าถัดไปในชุดข้อมูลของเรา 4 มีคะแนน z (4-10) / 5.558 = -1.08 ซึ่งหมายความว่าค่า “4” คือค่าเบี่ยงเบนมาตรฐาน ที่ต่ำกว่า ค่าเฉลี่ย 1.08
ยิ่งค่าอยู่ห่างจากค่าเฉลี่ย ค่าสัมบูรณ์ของคะแนน z ก็จะยิ่งสูงขึ้นสำหรับค่านั้น
ตัวอย่างเช่น ค่า 3 อยู่ไกลจากค่าเฉลี่ยมากกว่าค่า 4 ซึ่งอธิบายว่าทำไม 3 จึงมีคะแนน z ที่มีค่าสัมบูรณ์มากกว่า