หมายถึงเรขาคณิต

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 6, 2023 สถิติ 0 ความคิดเห็น

ในบทความนี้ เราจะอธิบายว่าค่าเฉลี่ยเรขาคณิตคืออะไร วิธีคำนวณ และความแตกต่างระหว่างค่าเฉลี่ยเรขาคณิตกับค่าเฉลี่ยเลขคณิต นอกจากนี้คุณยังสามารถดูแบบฝึกหัดที่แก้ไขได้ทีละขั้นตอนของค่าเฉลี่ยเรขาคณิต และคุณสมบัติของค่าเฉลี่ยประเภทนี้มีอะไรบ้าง สุดท้ายคุณจะพบเครื่องคิดเลขสำหรับคำนวณค่าเฉลี่ยเรขาคณิตของชุดข้อมูลใดๆ

ค่าเฉลี่ยเรขาคณิตคืออะไร?

ค่าเฉลี่ยเรขาคณิตคือการวัดความเป็นศูนย์กลางของสถิติเชิงพรรณนา ค่าเฉลี่ยเรขาคณิตของชุดข้อมูลทางสถิติเท่ากับรากที่ n ของผลิตภัณฑ์ของค่าทั้งหมด

ค่าเฉลี่ยเรขาคณิตใช้ในด้านการเงินธุรกิจเพื่อคำนวณอัตราผลตอบแทน เปอร์เซ็นต์ค่าเฉลี่ย และดอกเบี้ยทบต้น

สูตรสำหรับค่าเฉลี่ยเรขาคณิตจึงเป็นดังนี้:

ค่าเฉลี่ยเรขาคณิตสามารถคำนวณได้เมื่อข้อมูลทั้งหมดในตัวอย่างเป็นบวกเท่านั้น เพราะถ้าค่าเป็นลบ รากก็จะมีคำตอบเป็นลบหรือไม่มีคำตอบ ในทางกลับกัน ถ้าข้อมูลเป็นศูนย์ การคูณข้อมูลก็จะได้ศูนย์ ดังนั้น ค่าเฉลี่ยเรขาคณิตจะเท่ากับ 0

ค่าเฉลี่ยเรขาคณิตไม่ใช่ค่าเฉลี่ยประเภทเดียวที่มีอยู่ ยังมีค่าเฉลี่ยเลขคณิต ค่าเฉลี่ยถ่วงน้ำหนัก ค่าเฉลี่ยกำลังสอง และค่าเฉลี่ยฮาร์มอนิกอีกด้วย

ความแตกต่างระหว่างค่าเฉลี่ยเรขาคณิตและค่าเฉลี่ยเลขคณิต

ความแตกต่างที่สำคัญระหว่างค่าเฉลี่ยเรขาคณิตและค่าเฉลี่ยเลขคณิต ก็คือ ค่าเฉลี่ยเรขาคณิตมีความไวต่อค่าสุดขั้วน้อยกว่าค่าเฉลี่ยเลขคณิต นอกจากนี้ ค่าเฉลี่ยเลขคณิตสามารถคำนวณได้ด้วยค่าลบและศูนย์ ในขณะที่ค่าเฉลี่ยเรขาคณิตสามารถคำนวณได้ด้วยค่าบวกเท่านั้น

ในทำนองเดียวกัน ค่าเฉลี่ยเรขาคณิตโดยทั่วไปจะต่ำกว่าค่าเฉลี่ยเลขคณิตของชุดข้อมูลเดียวกัน

ควรสังเกตด้วยว่าการคำนวณค่าเฉลี่ยเรขาคณิตนั้นซับซ้อนกว่า ดังนั้นนัยสำคัญทางสถิติจึงตีความได้ยากกว่า

กล่าวโดยสรุป ค่าเฉลี่ยเรขาคณิตมีข้อดีและข้อเสียเมื่อเปรียบเทียบกับค่าเฉลี่ยเลขคณิต และการคำนวณค่าเฉลี่ยนี้หรือค่าเฉลี่ยนั้นจะขึ้นอยู่กับลักษณะของข้อมูล

วิธีการคำนวณค่าเฉลี่ยเรขาคณิต

ในการคำนวณค่าเฉลี่ยเรขาคณิต จะต้องดำเนินการตามขั้นตอนต่อไปนี้:

คำนวณผลคูณของข้อมูลทางสถิติทั้งหมดในตัวอย่าง
ค้นหารากที่ n ของผลิตภัณฑ์จากการคำนวณ
ผลลัพธ์ที่ได้คือค่าเฉลี่ยเรขาคณิตของตัวอย่างทางสถิติ

อย่างที่คุณเห็น การหาค่าเฉลี่ยเรขาคณิตของชุดข้อมูลนั้นค่อนข้างง่ายด้วยเครื่องคิดเลขหรือโปรแกรมคอมพิวเตอร์ เนื่องจากคุณเพียงแค่ต้องคำนวณผลคูณและรากเท่านั้น ในทางตรงกันข้ามการคำนวณด้วยมือค่อนข้างลำบาก

👉 นี่คือเหตุผลที่เราแนะนำให้ใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเฉลี่ยเรขาคณิตของชุดข้อมูล

ตัวอย่างค่าเฉลี่ยเรขาคณิต

เมื่อเราได้เห็นทฤษฎีเกี่ยวกับค่าเฉลี่ยเรขาคณิตแล้ว เราจะยกตัวอย่างเพื่อให้คุณเห็นว่าจะหาค่าเฉลี่ยเรขาคณิตได้อย่างไร

ทราบผลลัพธ์ทางเศรษฐกิจของบริษัทในช่วงห้าปีที่ผ่านมา ในปีแรกบริษัทสร้างผลกำไรทางเศรษฐกิจ 10% ในปีที่สองกำไรถึง 23% ในปีที่สามเงินที่ได้รับคือ 16% ในปีที่สี่ประสบความสำเร็จในการทำกำไรทางเศรษฐกิจ 7% และการลงทุน ในปีที่ห้าคิดเป็นผลตอบแทน 20% คุณจะถูกขอให้คำนวณค่าเฉลี่ยของเปอร์เซ็นต์ทั้งหมด

ดังที่เราได้เห็นแล้วว่า ในการคำนวณค่าเฉลี่ยของเปอร์เซ็นต์ คุณไม่ควรใช้ค่าเฉลี่ยเลขคณิต แต่ให้คำนวณโดยใช้ค่าเฉลี่ยเรขาคณิตแทน

ดังนั้นเราจึงใช้สูตรค่าเฉลี่ยเรขาคณิต:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

และเราแทนที่ค่าตัวอย่างลงในสูตรและทำการคำนวณ:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

โปรดทราบว่าเรามีจุดข้อมูลห้าจุด ดังนั้นเราจึงคำนวณรากที่ห้า

ผลลัพธ์ตัวเลขของค่าเฉลี่ยเรขาคณิตคือ 1.15 ซึ่งหมายความว่าบริษัทมีการเติบโตทางเศรษฐกิจโดยเฉลี่ย 15% ในแต่ละปี

โปรดทราบว่าเราสามารถหาค่าเฉลี่ยเรขาคณิตได้เนื่องจากค่าทั้งหมดเป็นค่าบวก แต่ถ้าเปอร์เซ็นต์ใดๆ ที่เป็นค่าลบ เราจะต้องใส่ข้อมูลในสูตรเป็นทศนิยมบวกพร้อมส่วนจำนวนเต็ม เท่ากับศูนย์ ตัวอย่างเช่น อัตราการเติบโต -30% ควรแสดงไว้ในสูตรเป็น 0.70 (1-0.3=0.7)

เครื่องคิดเลขเฉลี่ยทางเรขาคณิต

เสียบค่าสถิติตัวอย่างใดๆ ลงในเครื่องคิดเลขด้านล่างเพื่อหาค่าเฉลี่ยเรขาคณิต ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม โปรดจำไว้ว่าคุณไม่สามารถหาค่าเฉลี่ยทางเรขาคณิตได้หากค่านั้นเป็นลบหรือเป็นศูนย์

คุณสมบัติของค่าเฉลี่ยเรขาคณิต

ค่าเฉลี่ยเรขาคณิตมีลักษณะดังต่อไปนี้:

นี่คือค่าเฉลี่ยประเภทหนึ่งที่มีประโยชน์มากในการค้นหาค่าเฉลี่ยของเปอร์เซ็นต์หรือดัชนี

สามารถคำนวณได้หากข้อมูลทั้งหมดเป็นค่าบวกเท่านั้น

ความหมายทางเรขาคณิตของค่าเฉลี่ยเรขาคณิตของตัวเลข a และ b สองตัว คือด้านของสี่เหลี่ยมจัตุรัสที่มีพื้นที่เท่ากับสี่เหลี่ยมจัตุรัสซึ่งมีด้านวัด a และ b

$MG(a,b)=\sqrt{a\cdot b}$

ความหมายทางเรขาคณิตของค่าเฉลี่ยเรขาคณิตของตัวเลขสามตัว a , b และ c คือด้านของลูกบาศก์ซึ่งมีปริมาตรเท่ากับด้านขนานของด้าน a , b และ c

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

ลอการิทึมของค่าเฉลี่ยเรขาคณิตของชุดข้อมูลจะให้ค่าเฉลี่ยเลขคณิตของลอการิทึมของชุดเดียวกัน

ค่าเฉลี่ยเรขาคณิตของชุดค่าจะน้อยกว่าหรือเท่ากับค่าเฉลี่ยเลขคณิตเสมอ

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

ค่าเฉลี่ยเรขาคณิตแบบถ่วงน้ำหนักจะคำนวณในลักษณะเดียวกับค่าเฉลี่ยเรขาคณิต แต่โดยการเพิ่มน้ำหนักให้กับเลขชี้กำลังของแต่ละรายการข้อมูลเพื่อถ่วงน้ำหนักค่าทางสถิติ

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

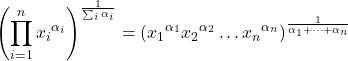
คำนวณค่าเฉลี่ยทางเรขาคณิตใน Excel

สุดท้าย เรามาดูวิธีการหาค่าเฉลี่ยเรขาคณิตของชุดข้อมูลโดยใช้โปรแกรม Excel กัน

ในการ คำนวณค่าเฉลี่ยเรขาคณิตใน Excel คุณต้องใช้ฟังก์ชัน MEANS.GEOM เพียงป้อนค่าทั้งหมดที่คุณต้องการหาค่าเฉลี่ยเรขาคณิต แล้วฟังก์ชันจะส่งกลับผลลัพธ์ค่าเฉลี่ยเรขาคณิต

ตัวอย่างเช่น หากต้องการหาค่าเฉลี่ยเรขาคณิตของตัวอย่างข้างต้น คุณต้องเขียนลงในกล่อง Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20)

คุณควรจำไว้ว่าหากค่าใดๆ ที่เป็นศูนย์หรือลบ ฟังก์ชันจะส่งกลับข้อผิดพลาด

อย่างที่คุณเห็นการคำนวณค่าเฉลี่ยเรขาคณิตด้วย Excel นั้นง่ายกว่าและเร็วกว่ามากเนื่องจากคุณเพียงแค่ต้องคัดลอกข้อมูลลงในแผ่นงานและใช้สูตร

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม