วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน sas
การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่
บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีดำเนินการ ANOVA แบบทางเดียวใน SAS
ขั้นตอนที่ 1: สร้างข้อมูล
สมมติว่านักวิจัยรับสมัครนักศึกษาจำนวน 30 คนเพื่อเข้าร่วมการศึกษาวิจัย นักเรียนจะ ถูกสุ่ม ให้ใช้วิธีการศึกษาแบบใดแบบหนึ่งจากสามวิธีเพื่อเตรียมตัวสอบ
ผลการสอบของนักเรียนแต่ละคนแสดงไว้ด้านล่าง:

เราสามารถใช้โค้ดต่อไปนี้เพื่อสร้างชุดข้อมูลนี้ใน SAS:
/*create dataset*/
data my_data;
input Method $Score;
datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;
ขั้นตอนที่ 2: ดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว
ต่อไป เราจะใช้ proc ANOVA เพื่อทำการวิเคราะห์ความแปรปรวนแบบทางเดียว:
/*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;
หมายเหตุ : เราใช้ฟังก์ชัน ค่าเฉลี่ย เพื่อระบุว่าควรทำการ ทดสอบหลังการทดสอบของ Tukey หากค่า p-value โดยรวมจากการวิเคราะห์ความแปรปรวนแบบทางเดียวมีนัยสำคัญทางสถิติ
ขั้นตอนที่ 3: ตีความผลลัพธ์
ตารางแรกที่เราต้องการวิเคราะห์ในผลลัพธ์คือตาราง ANOVA:

จากตารางนี้เราจะเห็น:
- ค่า F โดยรวม: 5.26
- ค่า p ที่สอดคล้องกัน: 0.0140
โปรดจำไว้ว่าการวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:
- H 0 : ค่าเฉลี่ยกลุ่มทั้งหมดเท่ากัน
- HA : ค่าเฉลี่ยกลุ่มอย่างน้อย 1 กลุ่มแตกต่างกัน พักผ่อน.
เนื่องจากค่า p ของตาราง ANOVA (0.0140) น้อยกว่า α = 0.05 เราจึงปฏิเสธสมมติฐานว่าง
สิ่งนี้บอกเราว่าคะแนนสอบเฉลี่ยของวิธีการศึกษาทั้งสามวิธีไม่เท่ากัน
ที่เกี่ยวข้อง: วิธีตีความค่า F และค่า P ใน ANOVA
SAS ยังมี Boxplots เพื่อแสดงภาพการกระจายผลการสอบสำหรับแต่ละวิธีการศึกษาทั้งสามวิธี:
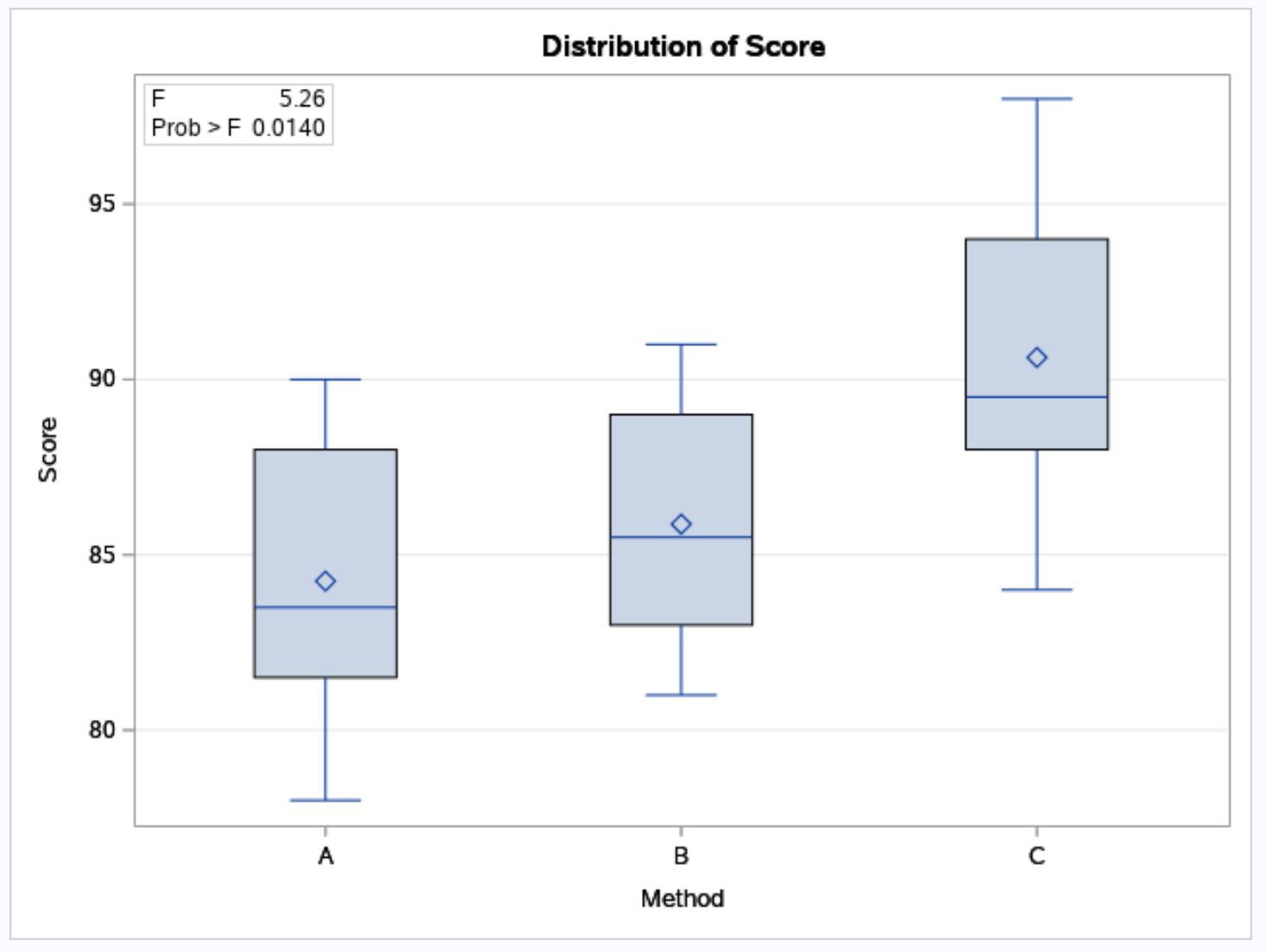
จากแผนภาพกล่อง เราจะเห็นว่าคะแนนสอบมีแนวโน้มสูงกว่าในกลุ่มนักเรียนที่ใช้วิธีการเรียนแบบ C เมื่อเทียบกับวิธี B และ C
เพื่อพิจารณาว่าค่าเฉลี่ยของกลุ่มใดที่แตกต่างกัน เราต้องอ้างอิงตารางผลลัพธ์สุดท้ายซึ่งแสดงผลการทดสอบหลังการทดสอบของ Tukey:
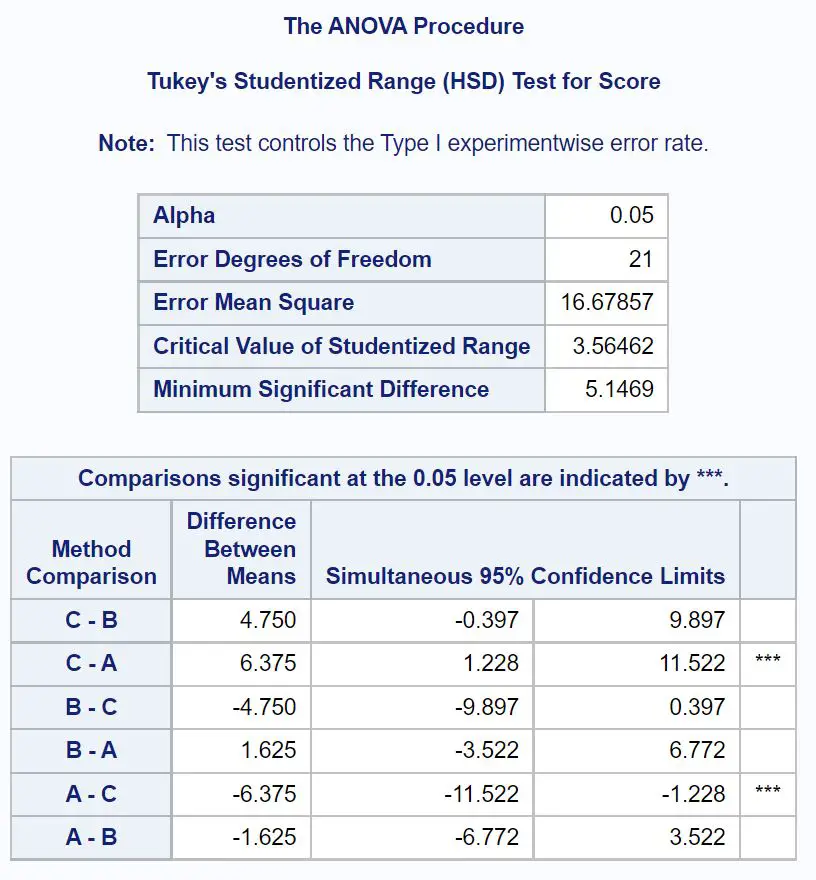
หากต้องการทราบว่าค่าเฉลี่ยของกลุ่มใดแตกต่างกัน เราต้องดูว่าการเปรียบเทียบแบบคู่ใดมีดาว ( *** ) อยู่ข้างๆ
ตารางแสดงให้เห็นว่าค่าเฉลี่ยของกลุ่ม A และ C แตกต่างกันอย่างมีนัยสำคัญทางสถิติ
นอกจากนี้เรายังสามารถดูช่วงความเชื่อมั่น 95% สำหรับความแตกต่างของคะแนนสอบเฉลี่ยระหว่างกลุ่ม A และ C:
ช่วงความเชื่อมั่น 95% สำหรับผลต่างเฉลี่ย: [1.228, 11.522]
ขั้นตอนที่ 4: รายงานผลลัพธ์
สุดท้ายนี้ เราสามารถ รายงานผลลัพธ์ ของการวิเคราะห์ความแปรปรวนแบบทางเดียวได้:
ทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อเปรียบเทียบผลของวิธีการศึกษาที่แตกต่างกันสามวิธีต่อผลการทดสอบ
การวิเคราะห์ความแปรปรวนแบบทางเดียวเปิดเผยว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในคะแนนสอบเฉลี่ยระหว่างอย่างน้อยสองกลุ่ม (F(2,21) = [5.26], p = 0.014)
การทดสอบ HSD ของ Tukey สำหรับการเปรียบเทียบหลายรายการพบว่าค่าเฉลี่ยของคะแนนสอบแตกต่างกันอย่างมีนัยสำคัญระหว่างวิธี C และวิธี A (95% CI = [1.228, 11.522])
ไม่มีความแตกต่างที่มีนัยสำคัญทางสถิติในคะแนนสอบเฉลี่ยระหว่างวิธี A และวิธี B หรือระหว่างวิธี B และวิธี C
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบทางเดียว:
ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบทางเดียว
เครื่องคิดเลข ANOVA แบบทางเดียว
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวด้วยตนเอง