การแจกแจงแบบเบอร์นูลลีและการแจกแจงแบบทวินาม: อะไรคือความแตกต่าง?
ตัวแปรสุ่มจะ เป็นไปตาม การแจกแจงเบอร์นูลลี หากมีเพียงสองผลลัพธ์ที่เป็นไปได้: 0 หรือ 1
เช่น สมมุติว่าเราโยนเหรียญหนึ่งครั้ง ให้ พี . ซึ่งหมายความว่าความน่าจะเป็นที่จะลงจอดคือ 1- p
ดังนั้นเราสามารถเขียนได้ว่า:
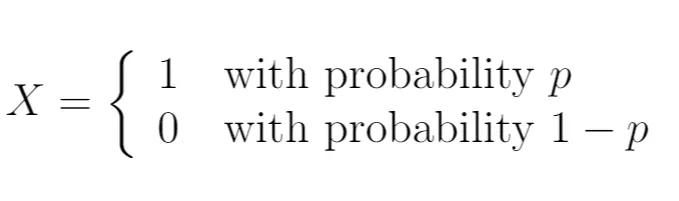
ในกรณีนี้ ตัวแปรสุ่ม X ตามหลังการแจกแจงเบอร์นูลลี สามารถรับค่าที่เป็นไปได้เพียงสองค่าเท่านั้น
ทีนี้ ถ้าเราพลิกเหรียญหลายครั้ง ผลรวมของตัวแปรสุ่มเบอร์นูลลีจะเป็นไปตามการแจกแจงแบบทวินาม
ตัวอย่างเช่น สมมติว่าเราโยนเหรียญ 5 ครั้งและต้องการทราบความน่าจะเป็นที่จะได้หัว k ครั้ง ดูเหมือนเป็นตัวแปร สุ่ม
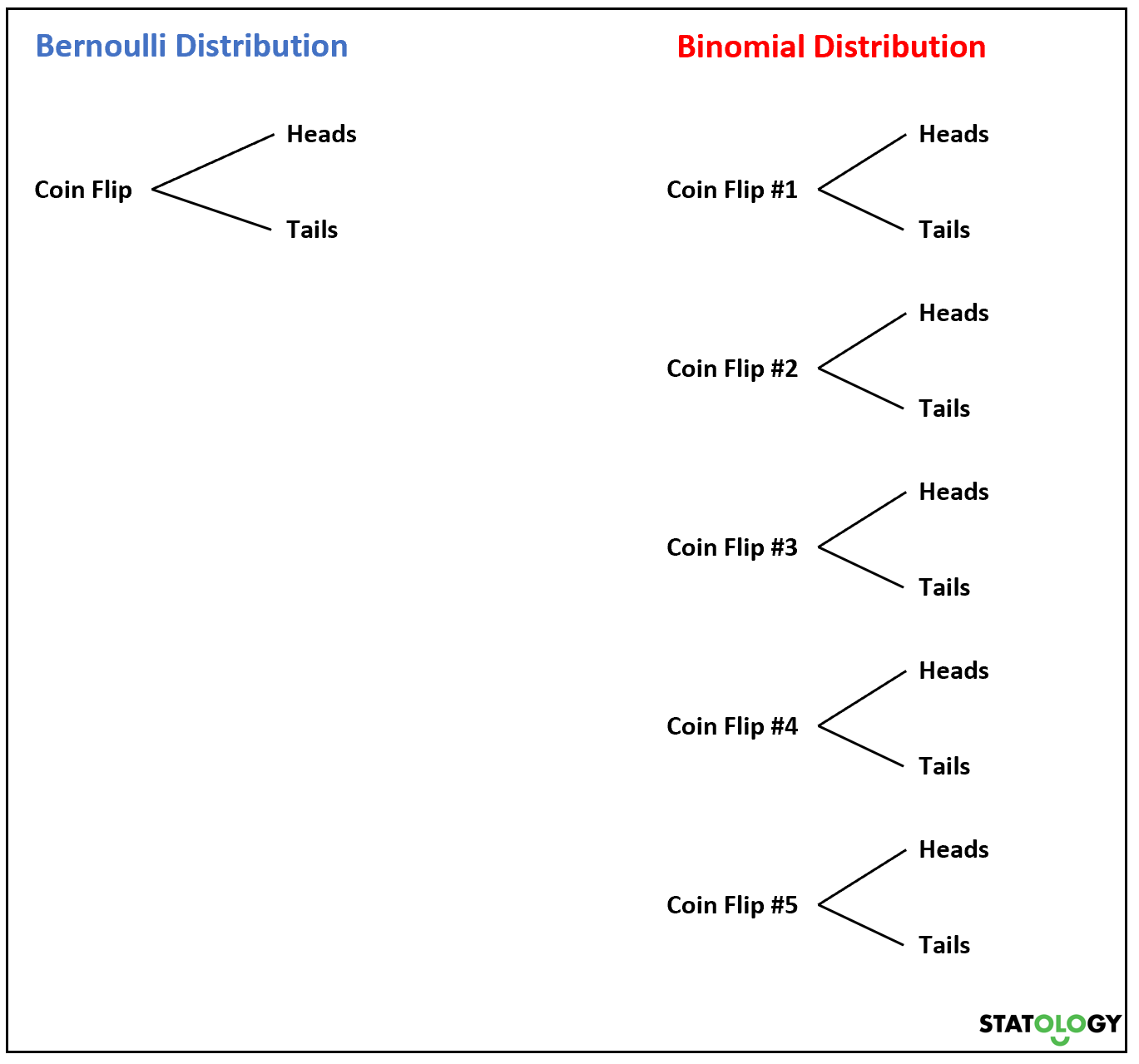
หากตัวแปรสุ่ม X เป็นไปตามการแจกแจงแบบทวินาม ความน่าจะเป็นที่ X = k สำเร็จจะพบได้จากสูตรต่อไปนี้:
P(X=k) = n C k * p k * (1-p) nk
ทอง:
- n: จำนวนการทดลอง
- k: จำนวนความสำเร็จ
- p: ความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองที่กำหนด
- n C k : จำนวนวิธีในการได้รับ k ความสำเร็จในการทดลอง n ครั้ง
เช่น สมมุติว่าเราโยนเหรียญ 3 ครั้ง เราสามารถใช้สูตรด้านบนเพื่อกำหนดความน่าจะเป็นที่จะได้หัว 0 ในระหว่างการพลิกทั้ง 3 ครั้ง:
P(X=0) = 3 C 0 * 0.5 0 * (1-0.5) 3-0 = 1 * 1 * (0.5) 3 = 0.125
เมื่อ n = 1 การทดลอง การแจกแจงแบบทวินามจะเท่ากับการแจกแจงแบบเบอร์นูลลี
หมายเหตุสำคัญ
ต่อไปนี้เป็นหมายเหตุสำคัญบางประการเกี่ยวกับการแจกแจงแบบแบร์นูลลีและทวินาม:
1. ตัวแปรสุ่มที่ตามหลังการแจกแจงแบบเบอร์นูลลีสามารถรับค่าที่เป็นไปได้ได้เพียงสองค่าเท่านั้น แต่ตัวแปรสุ่มที่ตามหลังการแจกแจงแบบทวินามสามารถรับค่าได้หลายค่า
เช่น ในการโยนเหรียญ 1 เหรียญ เราจะมีหัว 0 หรือ 1 หัว อย่างไรก็ตาม ในการเสมอกัน 5 ครั้ง เราอาจมีหัว 0, 1, 2, 3, 4 หรือ 5 ครั้ง
2. เพื่อให้ตัวแปรสุ่มเป็นไปตามการแจกแจงทวินาม ความน่าจะเป็นของ “ความสำเร็จ” ในการทดลองเบอร์นูลลีแต่ละครั้งจะต้องเท่ากันและเป็นอิสระ
ตัวอย่างเช่น ถ้าเรานิยาม “ความสำเร็จ” เป็นการหงายขึ้น ความน่าจะเป็นที่จะสำเร็จในการทอยแต่ละครั้งคือ 0.5 และการทอยแต่ละครั้งมีความเป็นอิสระ ผลลัพธ์ของการทอยจะไม่ส่งผลต่อผลลัพธ์ของการทอยครั้งต่อไป
แหล่งข้อมูลเพิ่มเติม
ความรู้เบื้องต้นเกี่ยวกับการทดลองทวินาม
ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบทวินาม
ทำความเข้าใจรูปร่างของการแจกแจงแบบทวินาม