วิธีเปรียบเทียบเส้นโค้ง roc สองเส้น (พร้อมตัวอย่าง)

วิธีหนึ่งในการแสดงภาพประสิทธิภาพของ แบบจำลองการจำแนกประเภท ในแมชชีนเลิร์นนิงคือการสร้าง เส้นโค้ง ROC ซึ่งย่อมาจากเส้นโค้ง “ลักษณะการทำงานของตัวรับ”

เส้นโค้งประเภทนี้แสดง ความไว และ ความเฉพาะเจาะจง ของแบบจำลองการจัดหมวดหมู่:

• ความไว: ความน่าจะเป็นที่แบบจำลองคาดการณ์ผลลัพธ์ที่เป็นบวกสำหรับการสังเกต เมื่อผลลัพธ์เป็นบวกจริงๆ
• ความจำเพาะ: ความน่าจะเป็นที่แบบจำลองทำนายผลลัพธ์ที่เป็นลบสำหรับการสังเกต เมื่อผลลัพธ์เป็นลบจริงๆ

แกน x ของเส้นโค้ง ROC แสดงถึง (1- ความจำเพาะ) และ แกน y แสดงถึง ความไว :

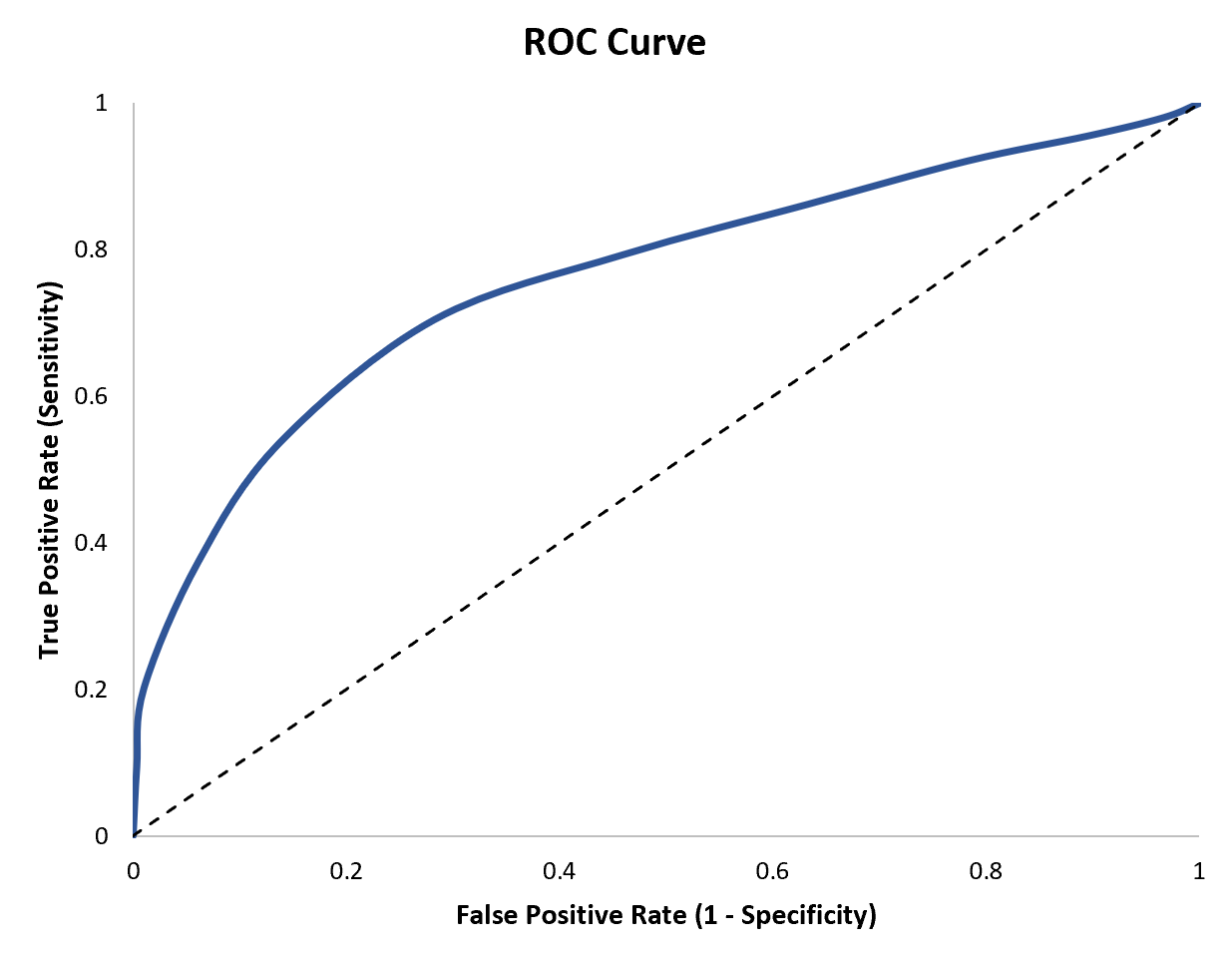
ยิ่งเส้นโค้ง ROC พอดีกับมุมซ้ายบนของพล็อตมากเท่าไร โมเดลก็ยิ่งสามารถจำแนกข้อมูลเป็นหมวดหมู่ได้ดีขึ้นเท่านั้น

ในการหาปริมาณ เราสามารถคำนวณ AUC (พื้นที่ใต้เส้นโค้ง) ซึ่งจะบอกเราว่าพล็อตอยู่ใต้เส้นโค้งมากเพียงใด

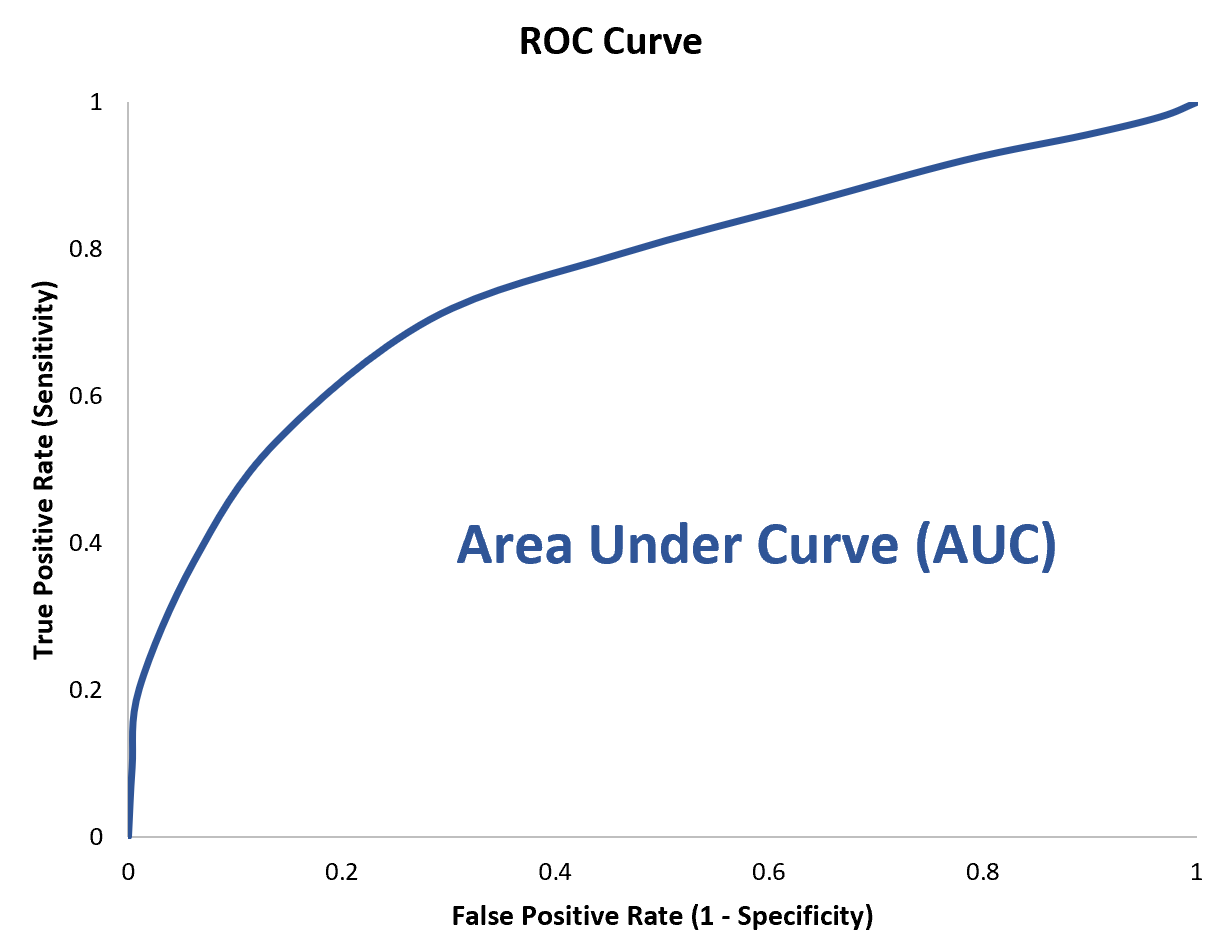
ยิ่ง AUC ใกล้ 1 มากเท่าใด โมเดลก็ยิ่งดีเท่านั้น

เมื่อเปรียบเทียบเส้นโค้ง ROC สองเส้นเพื่อพิจารณาว่าโมเดลการจำแนกประเภทใดดีกว่า เรามักจะดูว่าเส้นโค้ง ROC ใด “กอด” ใกล้กับมุมซ้ายบนของโครงเรื่องมากกว่า ดังนั้นจึงมีค่า AUC ที่สูงกว่า

ตัวอย่าง: วิธีเปรียบเทียบเส้นโค้ง ROC สองเส้น

สมมติว่าเราปรับแบบจำลองการถดถอยโลจิสติกและแบบจำลองการไล่ระดับสีเข้ากับชุดข้อมูลเพื่อทำนายผลลัพธ์ของตัวแปรตอบสนอง

สมมติว่าเราสร้างเส้นโค้ง ROC เพื่อให้เห็นภาพประสิทธิภาพของแต่ละรุ่น:

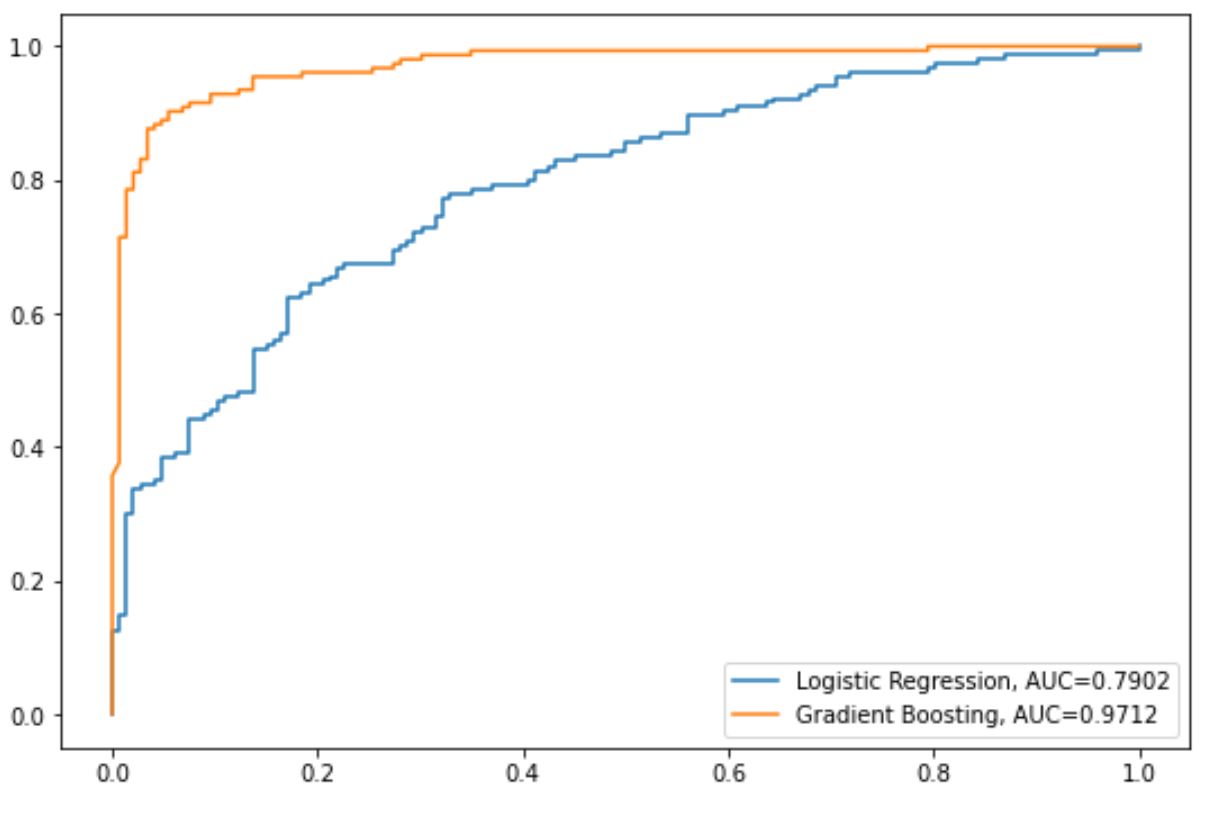
เส้นสีน้ำเงินแสดงเส้นโค้ง ROC สำหรับแบบจำลองการถดถอยโลจิสติก และเส้นสีส้มแสดงเส้นโค้ง ROC สำหรับแบบจำลองที่เน้นการไล่ระดับสี

จากแผนภูมิของเรา เราจะเห็นค่า AUC ต่อไปนี้สำหรับแต่ละรุ่น:

• AUC ของแบบจำลองการถดถอยโลจิสติก: 0.7902
• AUC ของแบบจำลองที่เสริมด้วยเกรเดียนต์: 0.9712

เนื่องจากแบบจำลองที่ปรับปรุงการไล่ระดับสีมีค่า AUC ที่สูงกว่า เราจึงบอกว่าแบบจำลองนี้ทำนายผลลัพธ์ของตัวแปรตอบสนองได้ดีขึ้น

หมายเหตุ : ในตัวอย่างนี้ เราเปรียบเทียบเส้นโค้ง ROC เพียงสองเส้นเท่านั้น แต่เป็นไปได้ที่จะปรับแบบจำลองการจำแนกประเภทที่แตกต่างกันหลายแบบให้พอดีกับชุดข้อมูล และเปรียบเทียบเส้นโค้ง ROC ได้มากขึ้นเพื่อกำหนดแบบจำลองที่ดีที่สุดที่จะใช้

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับแบบจำลองการจำแนกประเภทและเส้นโค้ง ROC:

รู้เบื้องต้นเกี่ยวกับการถดถอยโลจิสติก
วิธีการตีความเส้นโค้ง ROC
คะแนน AUC ที่ดีคืออะไร?