วิธีเปรียบเทียบแปลงกล่อง: พร้อมตัวอย่าง
พล็อตกล่อง คือประเภทของพล็อตที่แสดงข้อมูลสรุปห้าหลักของชุดข้อมูล ซึ่งประกอบด้วย:
- ค่าต่ำสุด
- ควอร์ไทล์ที่หนึ่ง (เปอร์เซ็นไทล์ที่ 25)
- ค่ามัธยฐาน
- ควอไทล์ที่สาม (เปอร์เซ็นไทล์ที่ 75)
- ค่าสูงสุด
ในการสร้างพล็อตกล่อง เราจะวาดกล่องจากควอไทล์ที่หนึ่งถึงควอไทล์ที่สาม ต่อไปเราวาดเส้นแนวตั้งที่ค่ามัธยฐาน สุดท้าย เราวาด “หนวด” ของควอไทล์จนถึงค่าต่ำสุดและสูงสุด

Boxplots มีประโยชน์เพราะช่วยให้เราเข้าใจการกระจายของค่าในชุดข้อมูลได้อย่างรวดเร็ว นอกจากนี้ยังมีประโยชน์สำหรับการเปรียบเทียบชุดข้อมูลสองชุดที่แตกต่างกันอีกด้วย
เมื่อเปรียบเทียบบ็อกซ์พล็อตสองรายการขึ้นไป เราสามารถตอบคำถามที่แตกต่างกันได้สี่ข้อ:
1. ค่ามัธยฐานเปรียบเทียบกันอย่างไร? เราสามารถเปรียบเทียบเส้นแนวตั้งในแต่ละช่องเพื่อดูว่าชุดข้อมูลใดมีค่ามัธยฐานที่สูงกว่า
2. การกระจายตัวเปรียบเทียบกันอย่างไร? เราสามารถเปรียบเทียบความยาวของแต่ละกล่อง (ซึ่งแสดงถึงระยะห่างระหว่าง Q1 และ Q3 ซึ่งเป็นช่วงระหว่างควอไทล์) เพื่อพิจารณาว่าชุดข้อมูลใดมีขนาดใหญ่กว่า
3. ความไม่สมมาตรเปรียบเทียบกันอย่างไร? ยิ่งเส้นแนวตั้งอยู่ใกล้กับไตรมาสแรกมากเท่าใด ชุดข้อมูลก็จะยิ่งบิดเบือนไปในทางบวกมากขึ้นเท่านั้น ยิ่งเส้นแนวตั้งอยู่ใกล้ไตรมาสที่สาม ชุดข้อมูลก็จะยิ่งบิดเบี้ยวมากขึ้น
4. มีค่าผิดปกติอยู่หรือไม่? ในแปลงกล่อง ค่าผิดปกติมักจะแสดงด้วยวงกลมเล็กๆ ที่ขยายออกไปเกินแต่ละหนวด การสังเกตถูกกำหนดให้เป็นค่าผิดปกติหากตรงตามเกณฑ์ข้อใดข้อหนึ่งต่อไปนี้:
- การสังเกตอย่างหนึ่งมีค่าน้อยกว่า Q1 – 1.5*IQR
- การสังเกตมีค่ามากกว่า Q3 + 1.5*IQR
ตัวอย่างต่อไปนี้แสดงวิธีเปรียบเทียบ Boxplots สองรายการที่แตกต่างกันและตอบคำถามสี่ข้อนี้
ตัวอย่าง: การเปรียบเทียบแปลงกล่อง
ชุดข้อมูลต่อไปนี้แสดงผลของนักเรียนที่ใช้เทคนิคการศึกษาแบบใดแบบหนึ่งจากสองเทคนิคเพื่อเตรียมตัวสำหรับการสอบ:
วิธีที่ 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91
วิธีที่ 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98
หากเราสร้าง boxplots สำหรับแต่ละชุดข้อมูล มันจะเป็นดังนี้:
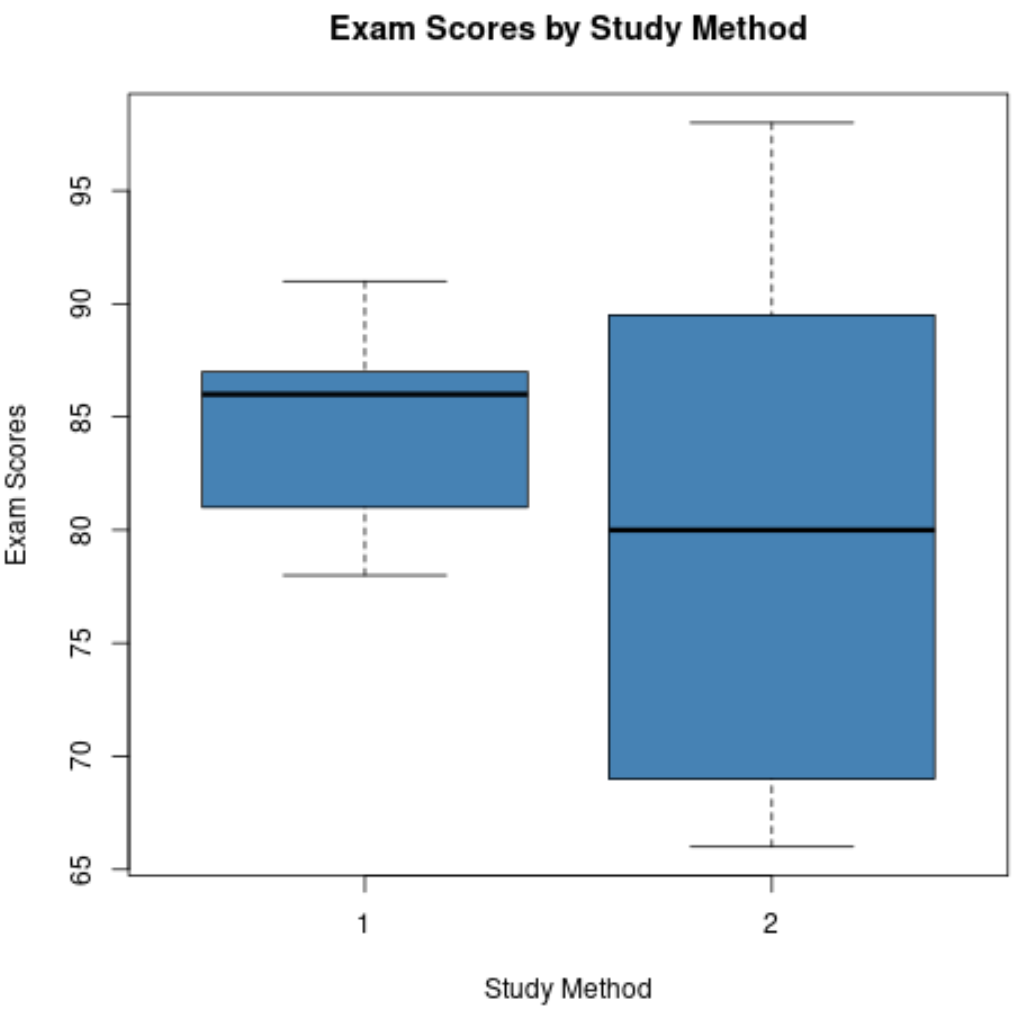
เราสามารถเปรียบเทียบ boxplots ทั้งสองนี้และตอบคำถามสี่ข้อต่อไปนี้:
1. ค่ามัธยฐานเปรียบเทียบกันอย่างไร? เส้นตรงกลางกล่องแปลงสำหรับวิธีเรียนที่ 1 สูงกว่าเส้นสำหรับเรียนวิธีที่ 2 แสดงว่านักเรียนที่ใช้วิธีเรียนแบบที่ 1 มีเกรดเฉลี่ยในการสอบที่สูงขึ้น
2. การกระจายตัวเปรียบเทียบกันอย่างไร? โครงเรื่องสำหรับวิธีเรียนที่ 2 ยาวกว่าวิธีเรียนแบบที่ 1 มาก ซึ่งบ่งชี้ว่าคะแนนสอบมีการกระจายในหมู่นักเรียนที่ใช้วิธีการเรียนแบบที่ 2 มากกว่ามาก
3. ความไม่สมมาตรเปรียบเทียบกันอย่างไร? เส้นตรงกลางกล่องพล็อตสำหรับวิธีเรียนที่ 1 ใกล้เคียงกับไตรมาสที่ 3 แสดงว่าการกระจายคะแนนสอบของนักเรียนที่ใช้วิธีเรียนที่ 1 เบี่ยงเบนไปในเชิงลบ ในทางกลับกัน เส้นตรงกลางกล่องพล็อตสำหรับวิธีที่ 2 ศึกษาจะอยู่ใกล้กับกึ่งกลางกล่อง ซึ่งหมายความว่าการกระจายตัวของคะแนนจะเอียงน้อยที่สุด
4. มีค่าผิดปกติอยู่หรือไม่? Boxplot ไม่มีวงกลมเล็กๆ ที่ขยายเกินขอบด้านบนหรือด้านล่าง ซึ่งหมายความว่าชุดข้อมูลทั้งสองไม่มีค่าผิดปกติที่ชัดเจน
แหล่งข้อมูลเพิ่มเติม
วิธีสร้างและตีความแปลงกล่องใน Excel
วิธีสร้างและตีความ Box Plots ใน SPSS
วิธีสร้างแปลงหลายกล่องใน R
วิธีสร้างและตีความ Box Plots ใน Stata