เมทริกซ์ความแปรปรวนร่วม

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าเมทริกซ์ความแปรปรวนร่วมคืออะไรและมีสูตรอะไร คุณจะค้นพบวิธีสร้างเมทริกซ์ความแปรปรวนร่วมด้วยตัวอย่างที่เป็นรูปธรรมและคุณสมบัติของเมทริกซ์ความแปรปรวนร่วม

เมทริกซ์ความแปรปรวนร่วมคืออะไร?

เมทริกซ์ความแปรปรวนร่วม คือเมทริกซ์จตุรัสที่มีองค์ประกอบคือความแปรปรวนและความแปรปรวนร่วมของตัวแปรที่ศึกษา ดังนั้น องค์ประกอบของเส้นทแยงมุมหลักของเมทริกซ์ความแปรปรวนร่วมคือความแปรปรวนของตัวแปรแต่ละตัว และองค์ประกอบที่เหลือคือความแปรปรวนร่วมระหว่างตัวแปร

ในทางสถิติ เมทริกซ์ความแปรปรวนร่วมใช้ในการวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรสุ่มตั้งแต่สองตัวขึ้นไป เมทริกซ์ความแปรปรวนร่วมมีประโยชน์มากเพราะช่วยให้คุณตีความความสัมพันธ์ระหว่างตัวแปรหลายตัวได้อย่างรวดเร็ว เนื่องจากคุณสามารถดูค่าของความแปรปรวนร่วมทั้งหมดของตัวแปรได้ในเวลาเดียวกัน

สัญลักษณ์สำหรับเมทริกซ์ความแปรปรวนร่วมคืออักษรกรีกตัวพิมพ์ใหญ่ซิกมา (Σ)

วิธีการคำนวณเมทริกซ์ความแปรปรวนร่วม

ในการ คำนวณเมทริกซ์ความแปรปรวนร่วม ของตัวแปรทางสถิติหลายตัว ต้องดำเนินการขั้นตอนต่อไปนี้:

คำนวณความแปรปรวนของตัวแปรทั้งหมด
คำนวณความแปรปรวนร่วมของตัวแปรแต่ละคู่
สร้างเมทริกซ์ความแปรปรวนร่วม:

ความแปรปรวนของตัวแปร i ต้องวางไว้บนเส้นทแยงมุมหลักของเมทริกซ์ โดยให้แม่นยำยิ่งขึ้นในตำแหน่ง i,i
ความแปรปรวนร่วมระหว่างตัวแปร i และ j ต้องอยู่ในตำแหน่ง i,j ของเมทริกซ์

สูตรสำหรับเมทริกซ์ความแปรปรวนร่วม จึงเป็นดังนี้:

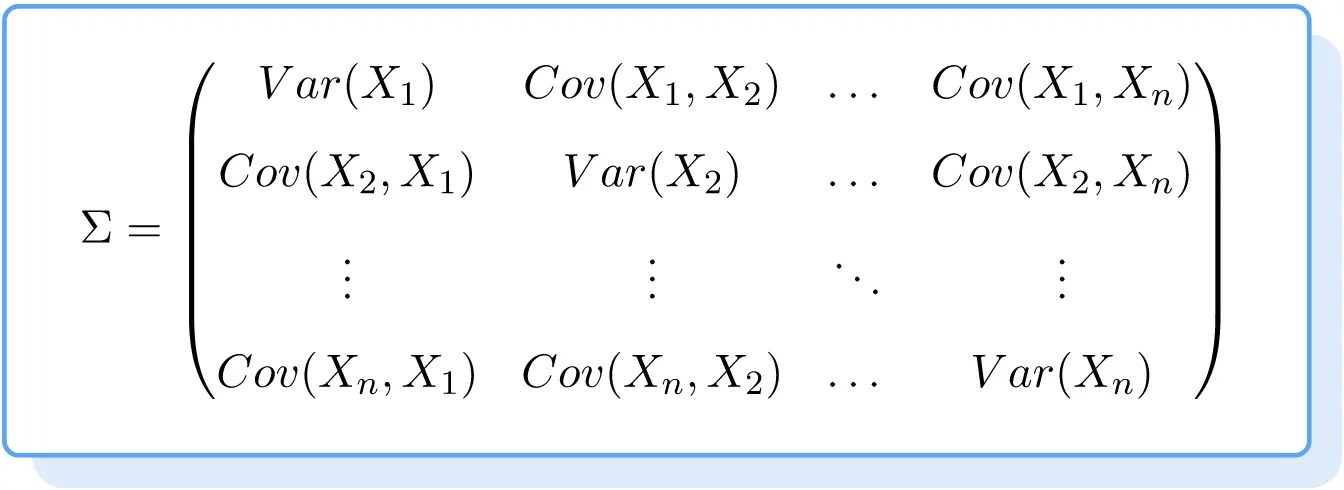
ตัวอย่างเมทริกซ์ความแปรปรวนร่วม

หลังจากดูคำจำกัดความของเมทริกซ์ความแปรปรวนร่วมแล้ว ด้านล่างนี้คือแบบฝึกหัดทีละขั้นตอนเพื่อให้คุณเห็นว่าเมทริกซ์ประเภทนี้เกิดขึ้นได้อย่างไร

คำนวณเมทริกซ์ความแปรปรวนร่วมของตัวแปร X, Y และ Z โดยมีค่าเป็น:

เอ็กซ์: 4, 7, 12, 5, 7
และ: 9, 15, 19, 6, 8
ซี: 7, 2, 4, 6, 3

สิ่งแรกที่เราต้องทำคือกำหนดค่าความแปรปรวนของตัวแปรทั้งหมด:

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ ดู: เครื่องคำนวณช่องว่าง

ประการที่สอง เราค้นหาความแปรปรวนร่วมระหว่างตัวแปรแต่ละคู่:

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ ดู: เครื่องคำนวณความแปรปรวนร่วม

และเมื่อเราคำนวณความแปรปรวนและความแปรปรวนร่วมทั้งหมดแล้ว สิ่งที่เหลืออยู่คือสร้างเมทริกซ์ความแปรปรวนร่วม ในการทำเช่นนี้ เราใส่ค่าความแปรปรวนบนเส้นทแยงมุมหลักของเมทริกซ์และค่าความแปรปรวนร่วมในตำแหน่งที่สอดคล้องกัน:

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

อย่างที่คุณเห็น การแสดงความแปรปรวนและความแปรปรวนร่วมในเมทริกซ์ ทำให้ตีความตัวแปรได้ง่ายมาก ตัวแปรที่มีการกระจายตัวมากที่สุดคือ Y (23.44) ในทางกลับกัน ตัวแปร X และ Y มีความสัมพันธ์โดยตรง ในขณะที่ตัวแปร X และ Z (และด้วยเหตุนี้ Y และ Z) จึงมีความสัมพันธ์แบบผกผัน

โปรดทราบว่าเมทริกซ์ความแปรปรวนร่วมจะสมมาตรเสมอ เนื่องจากความแปรปรวนร่วมระหว่างตัวแปรสองตัวไม่ได้ขึ้นอยู่กับลำดับของตัวแปร ตัวอย่างเช่น,

$Cov(X,Y)$

เท่ากับ

$Cov(Y,X).$

นอกจากนี้ เมทริกซ์ความแปรปรวนร่วมจะเป็นเมทริกซ์จัตุรัสเสมอและมิติของมันจะเท่ากับจำนวนตัวแปร ในกรณีนี้ เรามีตัวแปรสามตัว และนั่นคือสาเหตุว่าทำไมมันถึงเป็นเมทริกซ์ขนาด 3×3 แต่ถ้าเรามีเพียงสองตัวแปร เมทริกซ์ความแปรปรวนร่วมก็จะเป็น 2×2

คุณสมบัติของเมทริกซ์ความแปรปรวนร่วม

เมทริกซ์ความแปรปรวนร่วมมีลักษณะดังต่อไปนี้:

เมทริกซ์ความแปรปรวนร่วมคือเมทริกซ์จตุรัสลำดับของจำนวนตัวแปร
เมทริกซ์ความแปรปรวนร่วมมีความสมมาตร ซึ่งหมายความว่าเส้นทแยงมุมหลักของเมทริกซ์นั้นเป็นแกนสมมาตร
เมทริกซ์ความแปรปรวนร่วมจะเป็นค่ากึ่งแน่นอนเชิงบวกเสมอ
ดีเทอร์มิแนนต์ของเมทริกซ์ความแปรปรวนร่วมมีค่าเท่ากับหรือมากกว่าศูนย์

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม