วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน python
ความแปรปรวนร่วม คือการวัดว่าการเปลี่ยนแปลงในตัวแปรหนึ่งสัมพันธ์กับการเปลี่ยนแปลงในตัวแปรตัวที่สองอย่างไร โดยเฉพาะอย่างยิ่ง มันคือการวัดระดับที่ตัวแปรสองตัวมีความสัมพันธ์กันเชิงเส้นตรง
เมทริกซ์ความแปรปรวนร่วม คือเมทริกซ์จตุรัสที่แสดงความแปรปรวนร่วมระหว่างตัวแปรต่างๆ มากมาย นี่อาจเป็นวิธีที่มีประโยชน์ในการทำความเข้าใจว่าตัวแปรต่างๆ เกี่ยวข้องกันอย่างไรในชุดข้อมูล
ตัวอย่างต่อไปนี้แสดงวิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Python
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Python
ใช้ขั้นตอนต่อไปนี้เพื่อสร้างเมทริกซ์ความแปรปรวนร่วมใน Python
ขั้นตอนที่ 1: สร้างชุดข้อมูล
ขั้นแรก เราจะสร้างชุดข้อมูลที่ประกอบด้วยคะแนนสอบของนักเรียน 10 คนที่แตกต่างกันใน 3 วิชา ได้แก่ คณิตศาสตร์ วิทยาศาสตร์ และประวัติศาสตร์
import numpy as np math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95] science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94] history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78] data = np.array([math, science, history])
ขั้นตอนที่ 2: สร้างเมทริกซ์ความแปรปรวนร่วม
ต่อไป เราจะสร้างเมทริกซ์ความแปรปรวนร่วมสำหรับชุดข้อมูลนี้โดยใช้ฟังก์ชัน numpy cov() โดยระบุว่า bias = True เพื่อให้เราสามารถคำนวณเมทริกซ์ความแปรปรวนร่วมของประชากรได้
np.cov(data, bias= True )
array([[ 64.96, 33.2, -24.44],
[33.2, 56.4, -24.1],
[-24.44, -24.1, 75.56]])
ขั้นตอนที่ 3: ตีความเมทริกซ์ความแปรปรวนร่วม
ค่าตามเส้นทแยงมุมของเมทริกซ์เป็นเพียงความแปรปรวนของแต่ละเรื่อง ตัวอย่างเช่น:
- ความแปรปรวนของคะแนนคณิตศาสตร์คือ 64.96
- ความแปรปรวนของคะแนนวิทยาศาสตร์คือ 56.4
- ความแปรปรวนของคะแนนในอดีตคือ 75.56
ค่าอื่นๆ ของเมทริกซ์แสดงถึงความแปรปรวนร่วมระหว่างวิชาต่างๆ ตัวอย่างเช่น:
- ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และวิทยาศาสตร์คือ 33.2
- ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และประวัติศาสตร์คือ -24.44
- ความแปรปรวนร่วมระหว่างคะแนนวิทยาศาสตร์และประวัติศาสตร์คือ -24.1
จำนวนบวก สำหรับความแปรปรวนร่วมบ่งชี้ว่าตัวแปรสองตัวมีแนวโน้มเพิ่มขึ้นหรือลดลงตามกัน ตัวอย่างเช่น คณิตศาสตร์และวิทยาศาสตร์มีความแปรปรวนร่วมเชิงบวก (33.2) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในวิชาคณิตศาสตร์ก็มีแนวโน้มที่จะได้คะแนนสูงในวิชาวิทยาศาสตร์เช่นกัน ในทางกลับกัน นักเรียนที่มีผลการเรียนไม่ดีในวิชาคณิตศาสตร์ก็มักจะมีผลการเรียนไม่ดีในวิชาวิทยาศาสตร์เช่นกัน
จำนวนลบ สำหรับความแปรปรวนร่วมบ่งชี้ว่าเมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น ตัวแปรตัวที่สองมีแนวโน้มลดลง ตัวอย่างเช่น คณิตศาสตร์และประวัติศาสตร์มีความแปรปรวนร่วมเป็นลบ (-24.44) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในวิชาคณิตศาสตร์มักจะได้คะแนนต่ำในประวัติศาสตร์ ในทางกลับกัน นักเรียนที่ได้คะแนนคณิตศาสตร์ต่ำมักจะได้คะแนนสูงในประวัติศาสตร์
ขั้นตอนที่ 4: เห็นภาพเมทริกซ์ความแปรปรวนร่วม (ไม่บังคับ)
คุณสามารถเห็นภาพเมทริกซ์ความแปรปรวนร่วมได้โดยใช้ฟังก์ชัน heatmap() ของแพ็คเกจที่เกิดในทะเล:
import seaborn as sns import matplotlib.pyplot as plt cov = np.cov(data, bias=True) labs = ['math', 'science', 'history'] sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs) plt.show()
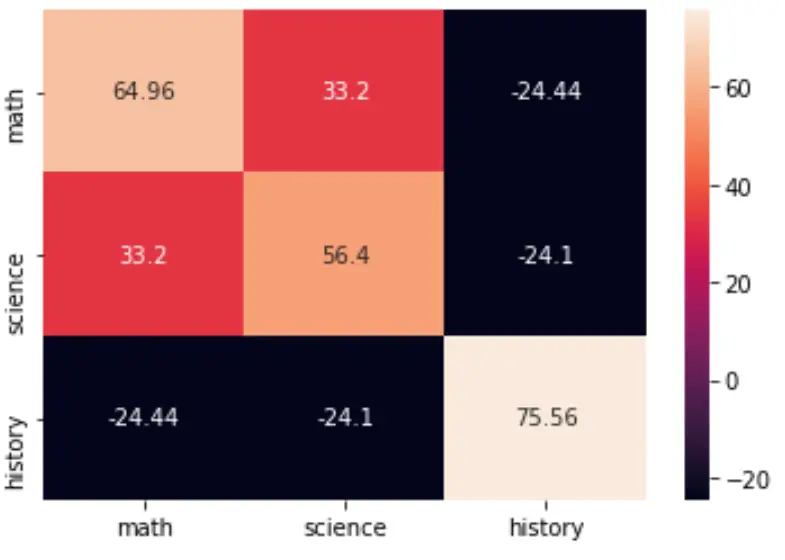
คุณยังสามารถเปลี่ยนจานสีได้โดยการระบุอาร์กิวเมนต์ cmap :
sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show()
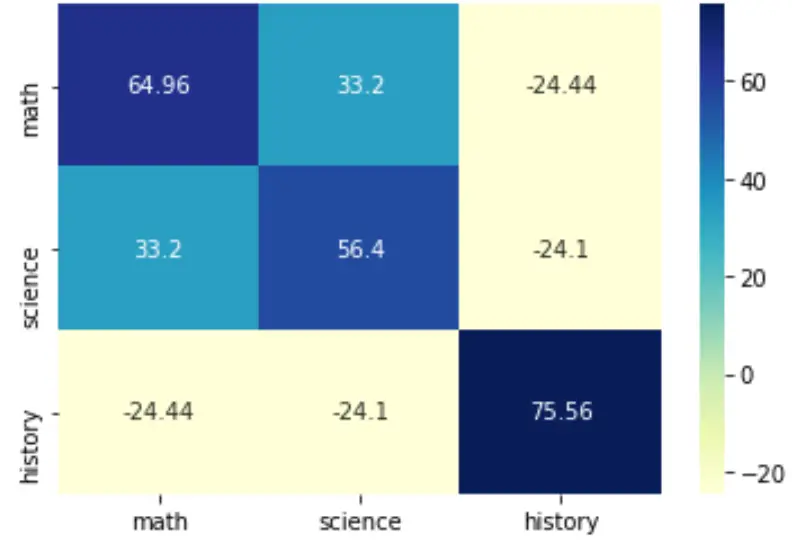
สำหรับรายละเอียดเพิ่มเติมเกี่ยวกับวิธีการจัดรูปแบบแผนที่ความร้อนนี้ โปรดดู เอกสารประกอบเกี่ยวกับทะเล