วิธีสร้างเมทริกซ์สหสัมพันธ์ใน r (4 ตัวอย่าง)
เมทริกซ์สหสัมพันธ์ คือตารางสี่เหลี่ยมที่แสดง ค่าสัมประสิทธิ์สหสัมพันธ์ ระหว่างตัวแปรในชุดข้อมูล
โดยให้วิธีที่รวดเร็วในการทำความเข้าใจจุดแข็งของความสัมพันธ์เชิงเส้นที่มีอยู่ระหว่างตัวแปรในชุดข้อมูล
มีสี่วิธีทั่วไปในการสร้างเมทริกซ์สหสัมพันธ์ใน R:
วิธีที่ 1: ฟังก์ชัน cor (เพื่อให้ได้เมทริกซ์อย่างง่ายของสัมประสิทธิ์สหสัมพันธ์)
cor(df)
วิธีที่ 2: ฟังก์ชัน rcorr (เพื่อรับค่า p ของสัมประสิทธิ์สหสัมพันธ์)
library (Hmisc)
rcorr( as.matrix (df))
วิธีที่ 3: ฟังก์ชัน Corrplot (เพื่อแสดงภาพเมทริกซ์สหสัมพันธ์)
library (corplot)
corrplot(cor(df))
วิธีที่ 4: ฟังก์ชัน ggcorrplot (เพื่อแสดงภาพเมทริกซ์สหสัมพันธ์)
library (ggcorrplot)
ggcorrplot(cor(df))
ตัวอย่างต่อไปนี้แสดงวิธีการใช้แต่ละวิธีกับกรอบข้อมูลต่อไปนี้ใน R:
#create data frame
df <- data. frame (assists=c(4, 5, 5, 6, 7, 8, 8, 10),
rebounds=c(12, 14, 13, 7, 8, 8, 9, 13),
points=c(22, 24, 26, 26, 29, 32, 20, 14))
#view data frame
df
assists rebound points
1 4 12 22
2 5 14 24
3 5 13 26
4 6 7 26
5 7 8 29
6 8 8 32
7 8 9 20
8 10 13 14
ตัวอย่างที่ 1: ฟังก์ชันคอร์
เราสามารถใช้ฟังก์ชัน R base cor() เพื่อสร้างเมทริกซ์สหสัมพันธ์ที่แสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างแต่ละตัวแปรในกรอบข้อมูลของเรา:
#create correlation matrix
cor(df)
assists rebound points
assists 1.0000000 -0.2448608 -0.3295730
rebounds -0.2448608 1.0000000 -0.5220917
points -0.3295730 -0.5220917 1.0000000
ค่าสัมประสิทธิ์สหสัมพันธ์ตามเส้นทแยงมุมของตารางมีค่าเท่ากับ 1 เนื่องจากตัวแปรแต่ละตัวมีความสัมพันธ์อย่างสมบูรณ์กับตัวมันเอง
ค่าสัมประสิทธิ์สหสัมพันธ์อื่นๆ ทั้งหมดบ่งบอกถึงความสัมพันธ์ระหว่างการรวมตัวแปรแบบคู่ต่างๆ ตัวอย่างเช่น:
- ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างการแอสซิสต์และการรีบาวด์คือ -0.245
- ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างแอสซิสต์และแต้มคือ -0.330
- ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างการรีบาวด์และคะแนนคือ -0.522
ตัวอย่างที่ 2: ฟังก์ชัน rcorr
เราสามารถใช้ฟังก์ชัน rcorr() จากแพ็คเกจ Hmisc ใน R เพื่อสร้างเมทริกซ์สหสัมพันธ์ที่แสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างแต่ละตัวแปรในกรอบข้อมูลของเรา:
library (Hmisc)
#create matrix of correlation coefficients and p-values
rcorr( as.matrix (df))
assists rebound points
assists 1.00 -0.24 -0.33
rebounds -0.24 1.00 -0.52
points -0.33 -0.52 1.00
n=8
P
assists rebound points
assists 0.5589 0.4253
rebounds 0.5589 0.1844
points 0.4253 0.1844
เมทริกซ์แรกแสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร และเมทริกซ์ที่สองแสดงค่า p ที่สอดคล้องกัน
ตัวอย่างเช่น ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างแอสซิสต์และการรีบาวน์คือ -0.24 และค่า p ของสัมประสิทธิ์สหสัมพันธ์นี้คือ 0.5589
สิ่งนี้บอกเราว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นเป็นลบ แต่ไม่มีความสัมพันธ์ที่มีนัยสำคัญทางสถิติเนื่องจากค่า p ไม่น้อยกว่า 0.05
ตัวอย่างที่ 3: ฟังก์ชัน Corrplot
เราสามารถใช้ฟังก์ชัน corrplot() จากแพ็คเกจ corrplot ใน R เพื่อให้เห็นภาพเมทริกซ์สหสัมพันธ์:
library (corplot)
#visualize correlation matrix
corrplot(cor(df))
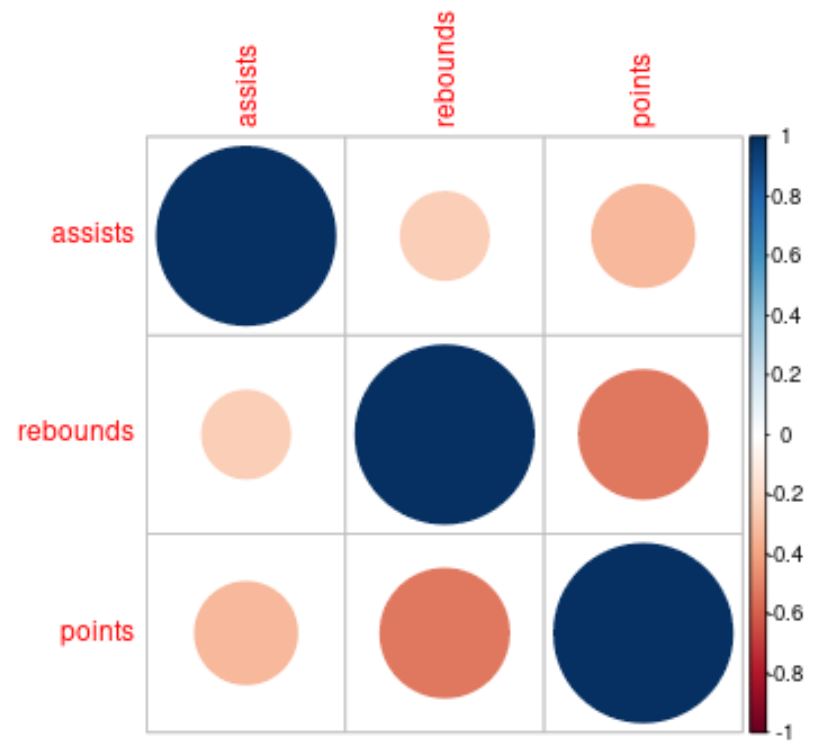
สีและขนาดของวงกลมในเมทริกซ์สหสัมพันธ์ช่วยให้เราเห็นภาพความสัมพันธ์ระหว่างตัวแปรแต่ละตัว
ตัวอย่างเช่น วงกลมที่ตัวแปรแอสซิสต์และรีบาวด์ตัดกันมีขนาดเล็กและเป็นสีแดงอ่อน ซึ่งบอกเราว่าความสัมพันธ์นั้นอ่อนแอและเป็นลบ
ตัวอย่างที่ 4: ฟังก์ชัน Corrplot
เราสามารถใช้ฟังก์ชัน ggcorrplot() จากแพ็คเกจ ggcorrplot ใน R เพื่อแสดงภาพเมทริกซ์สหสัมพันธ์:
library (ggcorrplot)
#visualize correlation matrix
ggcorrplot(cor(df))
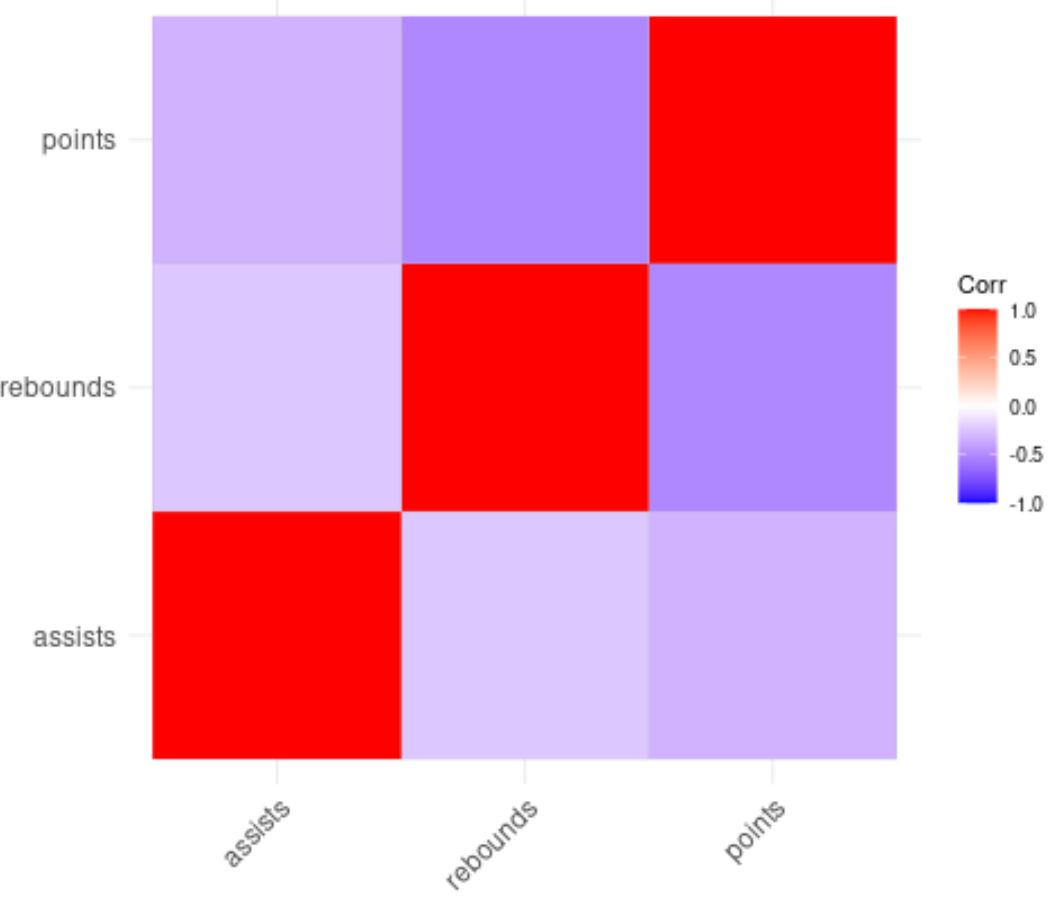
สีของสี่เหลี่ยมจัตุรัสในเมทริกซ์สหสัมพันธ์ช่วยให้เราเห็นภาพความสัมพันธ์ระหว่างตัวแปรแต่ละตัว
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:
วิธีการคำนวณความสัมพันธ์ของอันดับ Spearman ใน R
วิธีการคำนวณความสัมพันธ์บางส่วนใน R
วิธีการคำนวณความสัมพันธ์แบบเลื่อนใน R