เมื่อใดจึงควรใช้ความสัมพันธ์อันดับ spearman (2 สถานการณ์)

วิธีที่พบบ่อยที่สุดในการหาปริมาณความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัวคือการใช้ สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ซึ่ง จะใช้ค่าระหว่าง -1 ถึง 1 เสมอ โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้น
• 1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์

อย่างไรก็ตาม ค่าสัมประสิทธิ์สหสัมพันธ์ชนิดนี้ทำงานได้ดีที่สุดเมื่อความสัมพันธ์พื้นฐานที่แท้จริงระหว่างตัวแปรทั้งสองเป็น แบบเส้นตรง

มีค่าสัมประสิทธิ์สหสัมพันธ์อีกประเภทหนึ่งที่เรียกว่า สหสัมพันธ์อันดับสเปียร์แมน ซึ่งเหมาะที่สุดที่จะใช้ในสองสถานการณ์เฉพาะ:

สถานการณ์ที่ 1 : เมื่อทำงานกับข้อมูลที่เป็นความลับ

• ตัวอย่างอาจเป็นชุดข้อมูลที่มีการจัดอันดับคะแนนสอบคณิตศาสตร์ของนักเรียนและคะแนนสอบวิทยาศาสตร์ในชั้นเรียน

สถานการณ์ที่ 2 : เมื่อมีค่าผิดปกติสุดขั้วหนึ่งรายการขึ้นไป

• เมื่อชุดข้อมูลมีค่าผิดปกติอย่างมาก ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันจะได้รับผลกระทบอย่างมาก

ตัวอย่างต่อไปนี้แสดงวิธีคำนวณความสัมพันธ์อันดับ Spearman ในแต่ละสถานการณ์เหล่านี้

สถานการณ์ที่ 1: การเชื่อมโยงอันดับ Spearman กับข้อมูลอันดับ

พิจารณาชุดข้อมูลต่อไปนี้ (และแผนภาพกระจายที่สอดคล้องกัน) ที่แสดงความสัมพันธ์ระหว่างตัวแปรสองตัว:

เมื่อใช้ซอฟต์แวร์ทางสถิติ เราสามารถคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ต่อไปนี้สำหรับตัวแปรทั้งสองนี้:

• สหสัมพันธ์เพียร์สัน: 0.79
• ความสัมพันธ์อันดับสเปียร์แมน: 1

ในสถานการณ์นี้ ถ้าเราสนใจเฉพาะอันดับของค่าข้อมูล (เมื่ออันดับของ x เพิ่มขึ้น อันดับของ y จะเพิ่มขึ้นด้วยหรือไม่) ดังนั้นความสัมพันธ์ของอันดับของ Spearman จะทำให้เรามีแนวคิดที่ดีขึ้นเกี่ยวกับ ความสัมพันธ์ระหว่างตัวแปรทั้งสอง .

ในชุดข้อมูลนี้ เมื่ออันดับของ x เพิ่มขึ้น อันดับของ y จะเพิ่มขึ้น เสมอ

ความสัมพันธ์อันดับของสเปียร์แมนจับพฤติกรรมนี้ได้อย่างสมบูรณ์แบบโดยบอกเราว่ามีความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ ( ρ = 1 ) ระหว่างอันดับของ x และอันดับของ y

ในทางกลับกัน ความสัมพันธ์แบบเพียร์สันบอกเราว่ามีความสัมพันธ์เชิงเส้นตรงที่แข็งแกร่ง ( r = 0.79 ) ระหว่างตัวแปรทั้งสอง

นี่เป็นเรื่องจริง แต่จะไม่มีประโยชน์ถ้าเราสนใจแค่ความสัมพันธ์ระหว่างอันดับของ x และอันดับของ y

สถานการณ์ที่ 2: ความสัมพันธ์ของการจัดอันดับ Spearman กับค่าผิดปกติที่รุนแรง

พิจารณาชุดข้อมูลต่อไปนี้ (และแผนภาพกระจายที่สอดคล้องกัน) ที่แสดงความสัมพันธ์ระหว่างตัวแปรสองตัว:

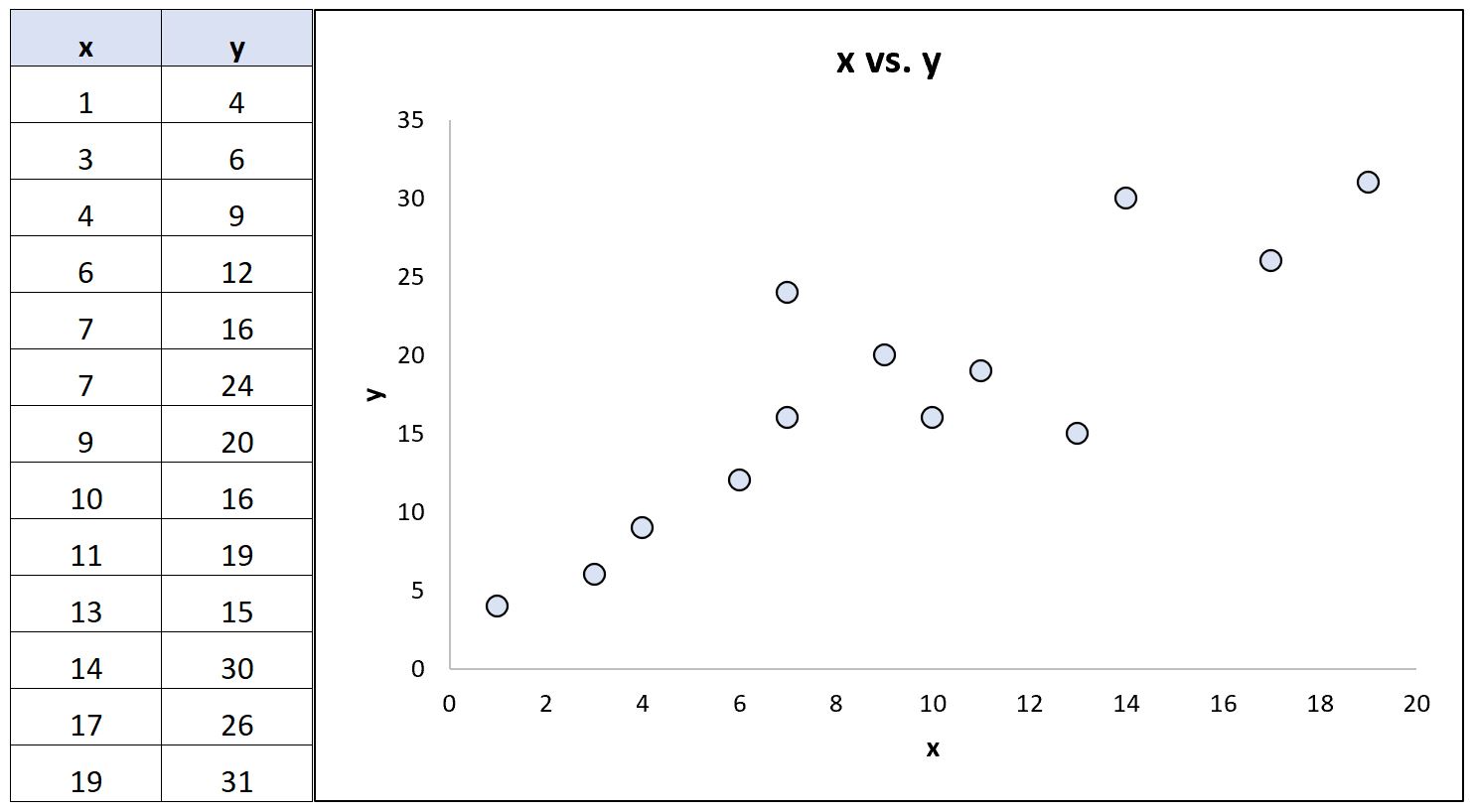
เมื่อใช้ซอฟต์แวร์ทางสถิติ เราสามารถคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ต่อไปนี้สำหรับตัวแปรทั้งสองนี้:

• สหสัมพันธ์เพียร์สัน: 0.86
• สหสัมพันธ์อันดับสเปียร์แมน: 0.85

ค่าสัมประสิทธิ์สหสัมพันธ์เกือบจะเหมือนกันเนื่องจากความสัมพันธ์พื้นฐานระหว่างตัวแปรต่างๆ นั้นเป็นเส้นตรงโดยประมาณ และไม่มีค่าผิดปกติที่รุนแรง

ตอนนี้ สมมติว่าเราเปลี่ยนค่า y สุดท้ายในชุดข้อมูลเพื่อให้มีค่าผิดปกติสุดขีด:

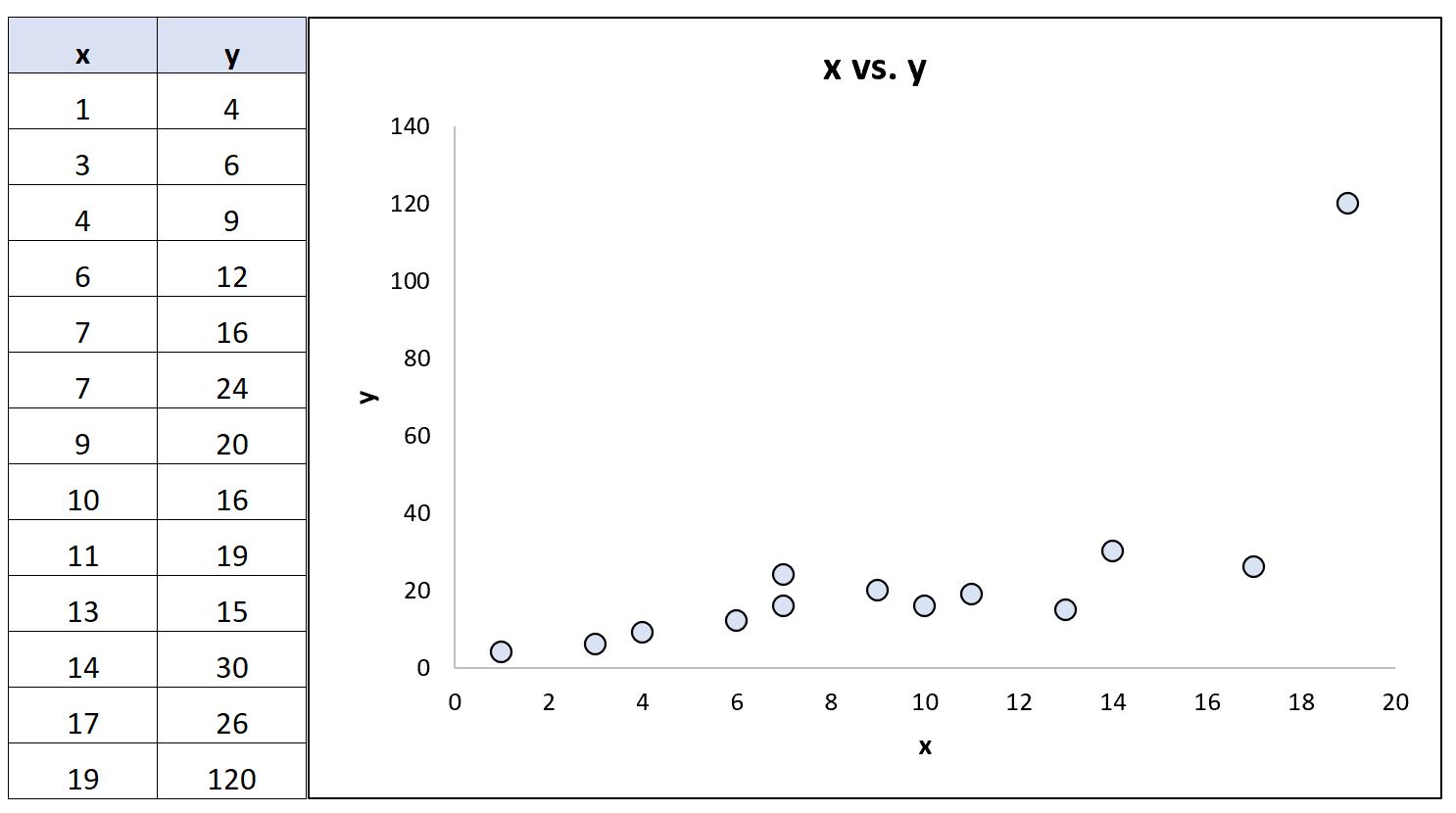
เมื่อใช้ซอฟต์แวร์ทางสถิติ เราสามารถคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ใหม่ได้:

• สหสัมพันธ์เพียร์สัน: 0.69
• สหสัมพันธ์อันดับสเปียร์แมน: 0.85

ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันเปลี่ยนแปลงอย่างมีนัยสำคัญ ในขณะที่ค่าสัมประสิทธิ์สหสัมพันธ์อันดับสเปียร์แมนยังคงเท่าเดิม

เมื่อใช้ศัพท์เฉพาะทางสถิติ เราจะบอกว่าความสัมพันธ์ระหว่าง x และ y เป็น แบบโมโนโทนิก (เมื่อ x เพิ่มขึ้น โดยทั่วไป y จะเพิ่มขึ้น) แต่ไม่ใช่เชิงเส้น เนื่องจากค่าผิดปกติมีอิทธิพลต่อข้อมูลอย่างมาก

ในสถานการณ์นี้ ความสัมพันธ์อันดับของสเปียร์แมนจะระบุปริมาณความสัมพันธ์แบบโมโนโทนิกนี้ได้ดี ในขณะที่ความสัมพันธ์ของเพียร์สันทำงานได้ไม่ดีนักเนื่องจากพยายามคำนวณความสัมพันธ์เชิงเส้นระหว่างตัวแปรทั้งสอง

ที่เกี่ยวข้อง: วิธีรายงานความสัมพันธ์ของอันดับ Spearman ในรูปแบบ APA

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีคำนวณความสัมพันธ์ของอันดับ Spearman โดยใช้ซอฟต์แวร์ต่างๆ:

วิธีการคำนวณความสัมพันธ์อันดับสเปียร์แมนใน Excel
วิธีการคำนวณความสัมพันธ์อันดับสเปียร์แมนใน Google ชีต
วิธีการคำนวณความสัมพันธ์ของอันดับ Spearman ใน R
วิธีการคำนวณความสัมพันธ์อันดับ Spearman ใน Python