แผนภาพเรเดียล (หรือแผนภาพสไปเดอร์)

บทความนี้จะอธิบายว่าแผนภูมิรัศมีหรือที่เรียกว่าแผนภูมิแมงมุมคืออะไร ดังนั้น คุณจะค้นพบว่ากราฟแนวรัศมีใช้ทำอะไร มีวิธีการอย่างไร ตัวอย่างที่เป็นรูปธรรมของการสร้างกราฟแนวรัศมี และสุดท้าย แผนภาพทางสถิติประเภทนี้มีข้อดีและข้อเสียอะไรบ้าง

แผนภูมิรัศมีคืออะไร?

แผนภูมิรัศมี หรือที่เรียกว่า แผนภูมิแมงมุม เป็นแผนภูมิทางสถิติประเภทหนึ่งที่แสดงตัวแปรต่างๆ นั่นคือในทางสถิติกราฟรัศมีใช้เพื่อเปรียบเทียบค่าของตัวแปรต่างๆ

นอกจากนี้ ข้อได้เปรียบหลักของแผนภูมิรัศมีคือมองเห็นได้ชัดเจน ทำให้เปรียบเทียบตัวแปรได้ง่ายและรวดเร็ว

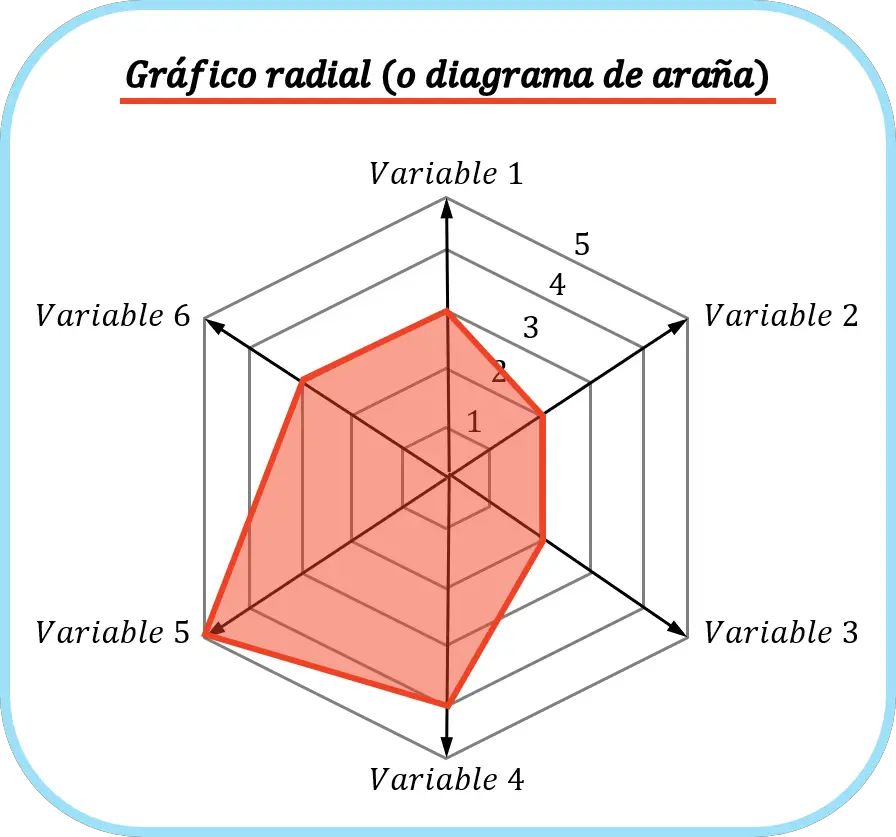
กราฟรัศมีเรียกอีกอย่างว่า กราฟเครือข่าย กราฟเชิงขั้ว หรือ กราฟดาว

วิธีสร้างแผนภูมิรัศมี

เมื่อพิจารณาจากคำจำกัดความของกราฟแนวรัศมี (หรือแผนภาพสไปเดอร์) เรามาดูกันว่ากราฟประเภทนี้เกิดขึ้นได้อย่างไร

1. สร้างรูปหลายเหลี่ยมปกติโดยให้มีด้านมากเท่าที่มีตัวแปรทางสถิติให้ศึกษา
2. สร้างรูปหลายเหลี่ยมประเภทเดียวกันมากขึ้นในขั้นตอนก่อนหน้าแต่มีขนาดต่างกัน เพื่อให้แต่ละรูปหลายเหลี่ยมแทนค่าที่แตกต่างกัน
3. จัดกึ่งกลางรูปหลายเหลี่ยมปกติในแนวตั้งและแนวนอน
4. แต่ละรัศมีของรูปหลายเหลี่ยมปกติจะสัมพันธ์กับแกนของตัวแปรที่แตกต่างกัน
5. วาดรูปหลายเหลี่ยมที่ไม่ปกติซึ่งแสดงถึงค่าของตัวแปรแต่ละตัว โดยให้แต่ละจุดยอดของรูปหลายเหลี่ยมที่ไม่ปกตินั้นเกิดขึ้นพร้อมกันบนแกนของตัวแปรแต่ละตัวด้วยค่าที่ตัวแปรดังกล่าวใช้
6. เพื่อให้เห็นภาพกราฟรัศมีได้ดีขึ้น คุณสามารถวาดภายในรูปหลายเหลี่ยมที่ไม่ปกติได้

ในทางกลับกัน ปัจจุบันมีโปรแกรมซอฟต์แวร์คอมพิวเตอร์มากมายที่ช่วยให้คุณสามารถสร้างกราฟแนวรัศมี เช่น Excel ได้อย่างรวดเร็ว

ตัวอย่างแผนภูมิรัศมี

• กราฟในกราฟรัศมี (หรือแผนภูมิแมงมุม) คะแนนที่บุคคลได้รับในเทอมนี้ในโรงเรียน:

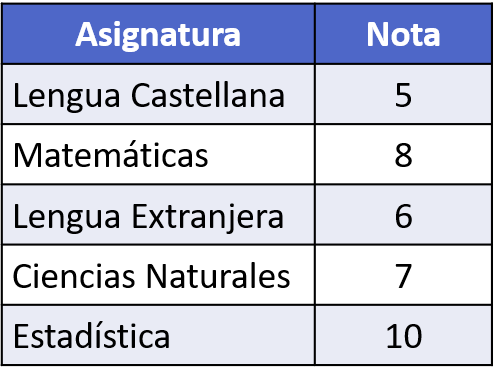
หลังจากทำตามขั้นตอนที่อธิบายไว้ข้างต้น การแสดงกราฟิกในแผนภูมิแมงมุมของชุดข้อมูลที่กำหนดจะเป็นดังนี้:

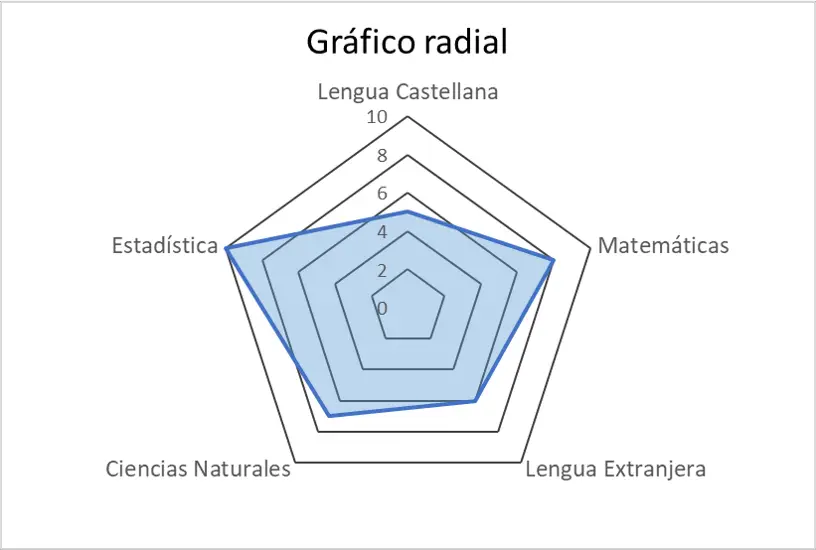
เมื่อเราสร้างกราฟรัศมีแล้ว เราจะตีความมัน ดังที่เห็นในแผนภาพ นักเรียนได้เกรดในวิชาดิจิทัลที่ดีกว่าในวิชาวรรณกรรม จากกราฟรัศมีจะเห็นได้ชัดเจนว่าคะแนนในด้านสถิติและคณิตศาสตร์สูงกว่าคะแนนในภาษา

ข้อดีและข้อเสียของแผนที่เรดาร์

เนื่องจากลักษณะของแผนภูมิรัศมี (หรือแผนภูมิดาว) จึงมีข้อดีและข้อเสียดังต่อไปนี้:

ข้อได้เปรียบ:

• นี่เป็นไดอะแกรมประเภทที่มองเห็นได้ชัดเจนและน่าดึงดูดใจมาก
• ช่วยให้คุณสามารถแสดงตัวแปรต่างๆ ในกราฟเดียวได้
• คุณสามารถเปรียบเทียบค่าของตัวแปรต่างๆ ได้อย่างรวดเร็ว

ข้อเสีย:

• บางครั้งอาจเป็นเรื่องยากที่จะทราบค่าที่แน่นอน
• เป็นการยากที่จะแสดงตัวแปรที่มีขนาดค่าแตกต่างกันมาก
• หากมีการแสดงตัวแปรหลายตัวในแผนภูมิรัศมี อาจมีแกนมากเกินไป ส่งผลให้อ่านแผนภูมิได้ยากขึ้น
• แผนภูมิรัศมีสามารถแสดงชุดข้อมูลได้เพียงไม่กี่ชุด เนื่องจากหากรูปหลายเหลี่ยมทับซ้อนกัน จะทำให้เข้าใจแผนภูมิได้ยาก
• มีเพียงข้อมูลเชิงปริมาณเท่านั้นที่สามารถแสดงเป็นแผนภูมิแมงมุมได้