แผนภาพวงกลม

ในบทความนี้ คุณจะได้เรียนรู้ว่าแผนภูมิวงกลมคืออะไร วิธีสร้างแผนภูมิวงกลม และแบบฝึกหัดทีละขั้นตอนสำหรับแผนภูมิประเภทนี้ นอกจากนี้ คุณจะสามารถดูได้ว่าคุณลักษณะของแผนภูมิวงกลมคืออะไร

แผนภูมิวงกลมคืออะไร?

แผนภูมิวงกลม หรือที่เรียกว่า แผนภูมิวงกลม เป็นแผนภูมิทางสถิติประเภทหนึ่งที่ใช้เพื่อแสดงเปอร์เซ็นต์และสัดส่วนด้วยภาพ แม่นยำยิ่งขึ้นในแผนภูมิวงกลม ข้อมูลจะถูกแสดงด้วยส่วนของวงกลม เพื่อให้มุมของ ชีส แต่ละชิ้นเป็นสัดส่วนกับความถี่ของมัน

ดังนั้น ยิ่งความถี่ของค่าสูง ส่วนแบ่งของค่านั้นก็จะยิ่งมากขึ้นในแผนภูมิวงกลม

ในด้านสถิติ แผนภูมิวงกลมมีประโยชน์อย่างมากในการแสดงข้อมูลเชิงคุณภาพบนกราฟ และยังช่วยให้คุณสรุปผลได้อย่างรวดเร็วอีกด้วย

ควรสังเกตว่าแผนภูมิวงกลมมีชื่อที่แตกต่างกันมากมาย เช่น แผนภูมิวงกลม แผนภูมิพิซซ่า แผนภูมิวงกลม แผนภูมิชีส หรือแม้แต่แผนภูมิ 360 องศา

วิธีทำแผนภูมิวงกลม

เมื่อพิจารณาถึงคำจำกัดความของแผนภูมิวงกลม ส่วนนี้จะแสดงวิธีสร้างแผนภูมิประเภทนี้:

1. รวบรวมข้อมูลทางสถิติและจัดทำตารางความถี่ที่สอดคล้องกัน
2. คำนวณมุมของแต่ละส่วนของกราฟด้วยสูตรต่อไปนี้



ทอง



คือมุมของเซกเตอร์ i



ความถี่สัมบูรณ์และ



จำนวนข้อมูลทั้งหมด

3. จากมุมที่คำนวณได้ ให้แสดงเซกเตอร์ต่างๆ บนกราฟวงกลมโดยใช้ไม้โปรแทรกเตอร์
4. คำนวณเปอร์เซ็นต์ของแต่ละเซกเตอร์ด้วยสูตรต่อไปนี้:



ทอง



คือเปอร์เซ็นต์ของเซกเตอร์ i



ความถี่สัมบูรณ์และ



จำนวนข้อมูลทั้งหมด

5. ระบุกราฟเปอร์เซ็นต์ของแต่ละภาคส่วน

ตัวอย่างแผนภูมิวงกลม

เพื่อให้คุณสามารถดูได้ว่าแผนภูมิวงกลมถูกสร้างขึ้นอย่างไร ฉันขอฝากตัวอย่างที่อธิบายไว้ทีละขั้นตอนด้านล่างไว้ให้คุณ

• มีผู้ถูกถาม 50 คนเกี่ยวกับเมืองโปรดของตน และข้อมูลได้รวบรวมไว้ในตารางต่อไปนี้ ลงจุดข้อมูลทางสถิตินี้บนแผนภูมิวงกลม

ก่อนอื่น คุณต้องหามุมที่สอดคล้องกับ ชีส แต่ละชนิด เมื่อต้องการทำเช่นนี้ เราใช้สูตรต่อไปนี้:

ตัวอย่างเช่น มุมที่สอดคล้องกับค่าแรกในตารางข้อมูลจะถูกคำนวณ:

เมื่อเรารู้มุมแล้ว ให้แสดงเซกเตอร์วงกลมโดยใช้ไม้โปรแทรกเตอร์:

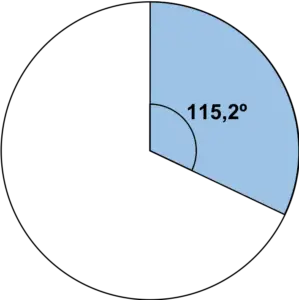
เราทำซ้ำขั้นตอนเดียวกันสำหรับค่าทั้งหมดในตาราง:

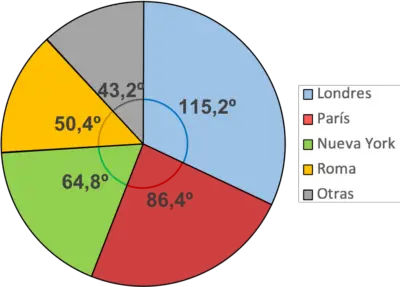
ขอแนะนำให้ระบายสีแต่ละส่วนเพื่อให้กราฟเข้าใจง่ายขึ้น ในทำนองเดียวกัน คุณควรเพิ่มคำอธิบายเพื่อแสดงความหมายของแต่ละสีในไดอะแกรม

หลังจากสร้างกราฟของ ชีส แล้ว เราจำเป็นต้องคำนวณเปอร์เซ็นต์ของชีสแต่ละชิ้นเพื่อใส่ลงในไดอะแกรม เมื่อต้องการทำเช่นนี้ เราใช้สูตรต่อไปนี้:

เปอร์เซ็นต์ของแต่ละภาคจึงเป็น:

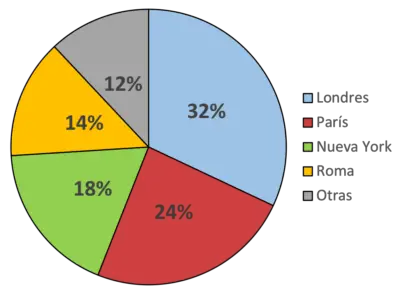
ด้วยแผนภูมิวงกลมนี้ เราระบุว่า ตัวอย่างเช่น สีน้ำเงินแสดงถึงเมืองลอนดอน และเป็นสถานที่ที่คนส่วนใหญ่ชอบ (32% ของผู้คน) ในทางกลับกัน สีเขียวแสดงถึงนิวยอร์ก ซึ่งเป็นเมืองโปรดของผู้ตอบแบบสอบถาม 18%

คุณสมบัติแผนภูมิวงกลม

ลักษณะของ Camembert มีดังนี้:

• แผนภูมิวงกลมมีประโยชน์มากในการแสดงข้อมูลเชิงคุณภาพ
• อย่างไรก็ตาม มีกราฟทางสถิติประเภทอื่นๆ ที่เหมาะสมกว่าในการแสดงตัวแปรเชิงปริมาณหรืออนุกรมเวลา
• นอกจากนี้ แผนภูมิวงกลมสามารถแสดงตัวแปรได้เพียงตัวแปรเดียว ซึ่งทำให้เปรียบเทียบตัวแปรได้ยาก
• แผนภูมิวงกลมมีภาพชัดเจน ช่วยให้วิเคราะห์และสรุปผลได้อย่างรวดเร็ว
• การอ่านแผนภูมิเป็นเรื่องยากเมื่อมีหลายภาคส่วนหรือบางส่วนมีขนาดเล็กมาก ในกรณีเช่นนี้ แนะนำให้จัดกลุ่มเซกเตอร์ขนาดเล็กออกเป็นเซกเตอร์เดียวที่เรียกว่า “อื่นๆ”