เกณฑ์ chauvenet: คำจำกัดความและตัวอย่าง

ค่าผิดปกติ คือ การสังเกต ที่อยู่ห่างจากค่าอื่นๆ ในชุดข้อมูลอย่างผิดปกติ ค่าผิดปกติอาจเป็นปัญหาได้เนื่องจากอาจส่งผลต่อผลลัพธ์ของการวิเคราะห์

วิธีหนึ่งในการระบุค่าผิดปกติในชุดข้อมูลคือการใช้ Chauvenet criterion ซึ่งใช้กระบวนการต่อไปนี้:

1. สำหรับแต่ละค่า x _i ในชุดข้อมูล ให้คำนวณค่าเบี่ยงเบนจากค่าเฉลี่ยดังนี้

ส่วนเบี่ยงเบน = |x _i – x | /วิ

โดยที่ x คือค่าเฉลี่ยตัวอย่าง และ s คือค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง

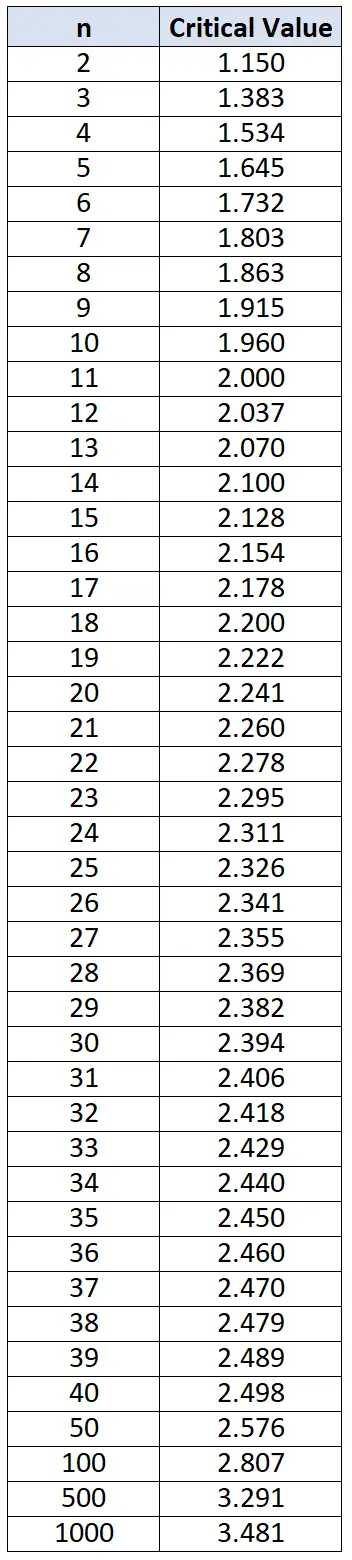
2. เปรียบเทียบค่าเบี่ยงเบนของแต่ละค่ากับค่าวิกฤตในตารางเกณฑ์ Chauvenet ด้านล่าง สำหรับค่าข้อมูลแต่ละรายการที่มีความเบี่ยงเบนมากกว่าที่พบในตาราง ให้รายงานค่าข้อมูลเหล่านี้เป็นค่าผิดปกติ

เกณฑ์ Chauvenet: ตัวอย่าง

สมมติว่าเรามีชุดข้อมูล 15 ค่าต่อไปนี้:

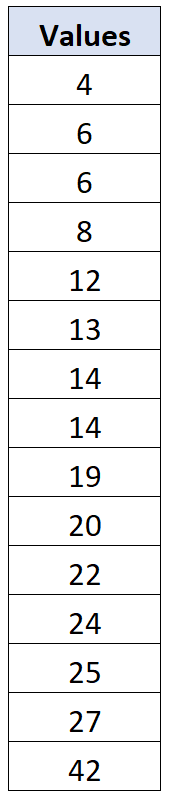
ค่าเฉลี่ยตัวอย่างสำหรับชุดข้อมูลนี้คือ x = 17.067 และค่าเบี่ยงเบนมาตรฐานตัวอย่างคือ s = 10.096 สำหรับค่าข้อมูลแต่ละค่า เราสามารถคำนวณค่าเบี่ยงเบนได้ดังนี้

ส่วนเบี่ยงเบน = |x _i – x | /วิ

ตัวอย่างเช่น:

• ค่าข้อมูลแรกจะมีการเบี่ยงเบน |4 – 17.067| / 10,096 = 1,294 .
• ค่าข้อมูลแรกจะมีการเบี่ยงเบน |6 – 17.067| / 10.096 = 1.096 .

และอื่นๆ

เราสามารถใช้สูตรเดียวกันในการคำนวณค่าเบี่ยงเบนของค่าข้อมูลแต่ละค่าได้:

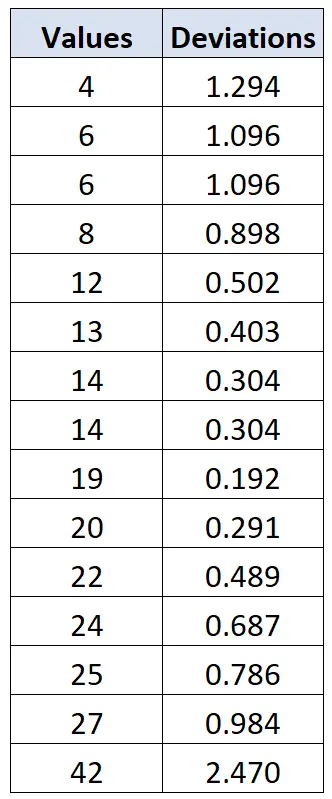
จากนั้น เราสามารถอ้างถึงตารางเกณฑ์ของ Chauvenet และสังเกตว่าค่าวิกฤตซึ่งสอดคล้องกับขนาดตัวอย่าง n=15 คือ 2.128 ดังนั้น ค่าใดๆ ที่มีค่าเบี่ยงเบนมากกว่า 2.128 ก็ถือเป็นค่าผิดปกติได้

ปรากฎว่าค่า 42 มีค่าเบี่ยงเบนมากกว่า 2.128:

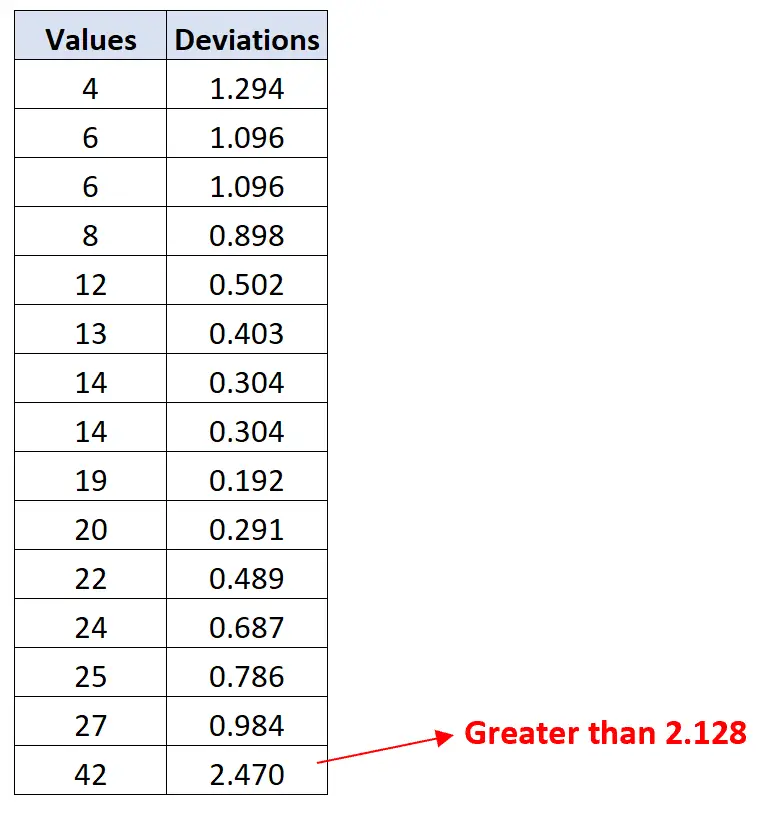
ดังนั้นค่า 42 จึงเป็นค่าผิดปกติเพียงค่าเดียวในชุดข้อมูลนี้

ข้อควรระวังเกี่ยวกับการใช้เกณฑ์ Chauvenet

เกณฑ์ Chauvenet ถือว่าค่าในชุดข้อมูลมี การกระจายตามปกติ หากไม่เป็นไปตามสมมติฐานนี้ การใช้เกณฑ์ Chauvenet เพื่อระบุค่าผิดปกติอาจไม่ถูกต้อง

หากคุณใช้วิธีนี้และพบว่าค่ามีค่าผิดปกติ คุณต้องตรวจสอบก่อนว่าค่านั้นไม่ได้เป็นผลมาจากข้อผิดพลาดในการป้อนข้อมูล บางครั้งข้อมูลก็ป้อนข้อมูลไม่ถูกต้อง

หากค่านั้นเป็นค่าผิดปกติจริงๆ คุณสามารถเลือกที่จะลบค่านั้นออกได้หากจะมีผลกระทบสำคัญต่อการวิเคราะห์โดยรวมของคุณ เพียงอย่าลืมระบุว่าคุณได้ลบค่าผิดปกติออกเมื่อรายงานผลลัพธ์ของคุณ

นอกจากนี้ ควรใช้วิธีนี้เพียงครั้งเดียวกับชุดข้อมูลที่กำหนด ตัวอย่างเช่น สมมติว่าเราใช้เกณฑ์นี้เพื่อระบุค่า 42 เป็นส่วนที่ผิดปกติในตัวอย่างก่อนหน้า และลบค่านั้นออกจากชุดข้อมูล

จากนั้นเราไม่ควรคำนวณ ค่าเฉลี่ยตัวอย่าง และค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างอีกครั้ง และคำนวณค่าเบี่ยงเบนอีกครั้งเพื่อหาค่าผิดปกติเพิ่มเติม