ละเว้นอคติของตัวแปร: คำจำกัดความและตัวอย่าง

อคติของตัวแปรที่ถูกละเว้น เกิดขึ้นเมื่อ ตัวแปรอธิบาย ที่เกี่ยวข้องไม่รวมอยู่ใน แบบจำลองการถดถอย ซึ่งอาจส่งผลให้เกิดอคติในค่าสัมประสิทธิ์ของตัวแปรอธิบายหนึ่งหรือหลายตัวในแบบจำลอง

ตัวแปรที่ถูกละเว้นมักถูกแยกออกจากแบบจำลองการถดถอยด้วยเหตุผลสองประการ:

1. ไม่มีข้อมูลสำหรับตัวแปร

2. ไม่ทราบผลกระทบของตัวแปรอธิบายต่อ ตัวแปรตอบสนอง

เพื่อให้ตัวแปรที่ละเว้นไปบิดเบือนค่าสัมประสิทธิ์ของโมเดลจริงๆ ต้องเป็นไปตามเงื่อนไขสองข้อต่อไปนี้:

1. ตัวแปรที่ถูกละเว้นจะต้องสัมพันธ์กับตัวแปรอธิบายตั้งแต่หนึ่งตัวขึ้นไปในแบบจำลอง

2. ตัวแปรที่ถูกละเว้นจะต้องสัมพันธ์กับตัวแปรตอบสนองในโมเดล

ผลกระทบของอคติตัวแปรที่ถูกละเว้น

สมมติว่าเรามีตัวแปรอธิบายสองตัวคือ A และ B และตัวแปรตอบสนอง Y สมมติว่าเราปรับโมเดลการถดถอยเชิงเส้นอย่างง่ายโดยมี A เป็นตัวแปรอธิบายเพียงตัวเดียว และปล่อย B ออกจากโมเดล

ถ้า B มีความสัมพันธ์กับ A และ มีความสัมพันธ์กับ Y จะส่งผลให้เกิดอคติในการประมาณค่าสัมประสิทธิ์ของ A แผนภาพต่อไปนี้แสดงให้เห็นว่าการประมาณค่าสัมประสิทธิ์ของ A จะมีอคติอย่างไร ขึ้นอยู่กับลักษณะของความสัมพันธ์กับ บี:

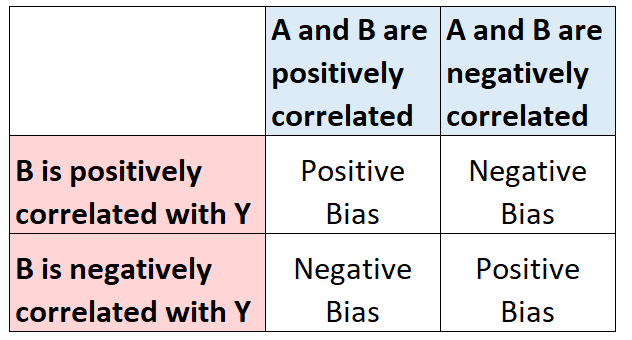
ตัวอย่าง: ละเว้นอคติของตัวแปร

สมมติว่าเราต้องการศึกษาผลกระทบของพื้นที่เป็นตารางฟุตต่อราคาอสังหาริมทรัพย์ ดังนั้นเราจึงใช้แบบจำลองการถดถอยเชิงเส้นอย่างง่ายต่อไปนี้

ราคาบ้าน = B ₀ + B ₁ (พื้นที่สี่เหลี่ยม)

สมมติว่าเราพบว่าแบบจำลองโดยประมาณคือ:

ราคาบ้าน = 40,203.91 + 118.31 (พื้นที่สี่เหลี่ยม)

วิธีที่เราตีความค่าสัมประสิทธิ์สำหรับพื้นที่เป็นตารางฟุตก็คือว่า การเพิ่มขึ้นอีก 1 หน่วยเป็นตารางฟุตจะสัมพันธ์กับการเพิ่มขึ้นของราคาบ้านโดยเฉลี่ย 118.31 ดอลลาร์

อย่างไรก็ตาม สมมติว่าเราละทิ้ง อายุ ตัวแปรที่อธิบายออกไป ซึ่งกลายเป็นความสัมพันธ์เชิงลบอย่างมากกับพื้นที่เป็นตารางฟุต และมีความสัมพันธ์เชิงลบอย่างมากกับราคาอสังหาริมทรัพย์ ตัวแปรนี้ควรอยู่ในโมเดล แต่ไม่ใช่ ดังนั้นการประมาณค่าสัมประสิทธิ์สำหรับพื้นที่เป็นตารางฟุตจึงมีความเอนเอียง

เนื่องจาก อายุ มีความสัมพันธ์เชิงลบกับทั้งตัวแปรอธิบายและการตอบสนองในแบบจำลอง เราจึงคาดว่าการประมาณค่าสัมประสิทธิ์สำหรับพื้นที่เป็นตารางฟุตจะมีอคติเชิงบวก:

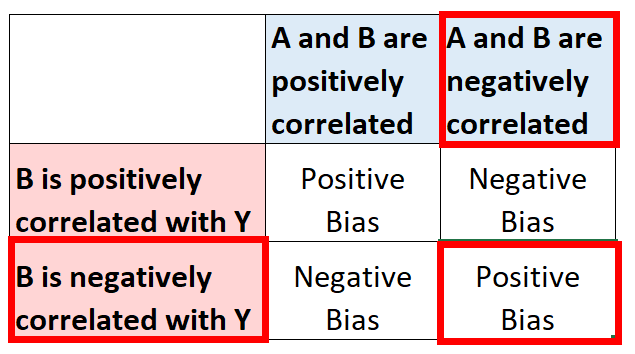
สมมติว่าเราค้นหาข้อมูลเกี่ยวกับอายุของที่อยู่อาศัยแล้วรวมไว้ในแบบจำลอง แบบจำลองจะกลายเป็น:

ราคาบ้าน = B ₀ + B ₁ (พื้นที่สี่เหลี่ยม) + B ₂ (อายุ)

สมมติว่าเราพบว่าแบบจำลองโดยประมาณคือ:

ราคาบ้าน = 123,426.20 + 81.06 (พื้นที่สี่เหลี่ยม) – 1,291.04 (อายุ)

โปรดทราบว่าการประมาณค่าสัมประสิทธิ์สำหรับพื้นที่เป็นตารางฟุตลดลงอย่างมาก ซึ่งหมายความว่า มี ความลำเอียงเชิงบวกในรุ่นก่อนหน้า

วิธีที่เราตีความค่าสัมประสิทธิ์พื้นที่เป็นตารางฟุตในแบบจำลองนี้คือ การเพิ่มขึ้นอีก 1 หน่วยเป็นตารางฟุตจะสัมพันธ์กับการเพิ่มขึ้นของราคาบ้านโดยเฉลี่ยที่ 81.06 ดอลลาร์ โดยสมมติว่าอายุคงที่

จะทำอย่างไรกับการละเว้นอคติตัวแปร

น่าเสียดายที่อคติของตัวแปรที่ถูกละเว้นมักเกิดขึ้นในโลกแห่งความเป็นจริง เนื่องจากโดยทั่วไปแล้วตัวแปรบางตัว ควร รวมอยู่ในแบบจำลองการถดถอย แต่ไม่ใช่เพราะไม่มีข้อมูลสำหรับตัวแปรเหล่านั้น หรือไม่ทราบความสัมพันธ์ระหว่างตัวแปรเหล่านั้นกับตัวแปรตอบสนอง

หากเป็นไปได้ คุณควรพยายามรวมตัวแปรอธิบายที่เกี่ยวข้องทั้งหมดไว้ในแบบจำลองการถดถอย เพื่อที่คุณจะได้เข้าใจความสัมพันธ์ที่แท้จริงระหว่างตัวแปรอธิบายและตัวแปรตอบสนอง

การยกเว้นตัวแปรอธิบายที่เกี่ยวข้องออกจากแบบจำลองอาจส่งผลกระทบอย่างมีนัยสำคัญต่อการตีความแบบจำลอง ดังที่เราเห็นในตัวอย่างก่อนหน้านี้เกี่ยวกับราคาอสังหาริมทรัพย์

แหล่งข้อมูลเพิ่มเติม

ตัวแปรที่ซ่อนอยู่คืออะไร?
ตัวแปรที่น่าสับสนคืออะไร?