วิธีการคำนวณความเบ้และความโด่งใน google ชีต
ในสถิติ ความเบ้ และ ความโด่ง เป็นสองวิธีในการวัดรูปร่างของการแจกแจง
ความเบ้ คือการวัดความเบ้ของการแจกแจง ค่านี้สามารถเป็นบวกหรือลบได้
- ความเบ้เชิงลบบ่งชี้ว่าส่วนท้ายอยู่ทางด้านซ้ายของการแจกแจง ซึ่งขยายไปสู่ค่าลบมากขึ้น
- การเอียงเชิงบวกบ่งชี้ว่าส่วนท้ายอยู่ทางด้านขวาของการแจกแจง ซึ่งขยายไปสู่ค่าบวกมากขึ้น
- ค่าศูนย์บ่งชี้ว่าไม่มีความไม่สมดุลในการแจกแจง ซึ่งหมายความว่าการแจกแจงมีความสมมาตรอย่างสมบูรณ์
Kurtosis เป็นตัววัดว่าการกระจายแบบหนักหรือแบบหางเบาเมื่อเทียบกับ การกระจายแบบปกติ
- ความโด่งของการแจกแจงแบบปกติคือ 3
- หากการแจกแจงแบบใดแบบหนึ่งมีความโด่งน้อยกว่า 3 ก็เรียกว่า แบบเพลย์เคิร์ก ซึ่งหมายความว่ามีแนวโน้มที่จะสร้างค่าผิดปกติที่รุนแรงน้อยลงและน้อยลงกว่าการแจกแจงแบบปกติ
- หากการกระจายแบบใดแบบหนึ่งมีความโด่งมากกว่า 3 ก็เรียกว่าเป็น โรคเลปโตเคอร์ติก ซึ่งหมายความว่ามีแนวโน้มที่จะสร้างค่าผิดปกติมากกว่าการกระจายแบบปกติ
บทแนะนำนี้จะอธิบายวิธีคำนวณทั้งความเบ้และความโด่งสำหรับชุดข้อมูลที่กำหนดใน Google ชีต
ตัวอย่าง: ความเบ้และความแบนใน Google ชีต
สมมติว่าเรามีชุดข้อมูลต่อไปนี้:
ในการคำนวณความเบ้และความโด่งของชุดข้อมูลนี้ เราสามารถใช้ฟังก์ชัน SKEW() และ KURT() โดยมีไวยากรณ์ต่อไปนี้:
- SKEW (ตารางค่า)
- KURT (ตารางค่า)
สิ่งสำคัญคือต้องทราบว่าฟังก์ชันใดฟังก์ชันหนึ่งจะส่งกลับ ข้อผิดพลาด #DIV/0! ในสองสถานการณ์ต่อไปนี้:
- หากมีจุดข้อมูลน้อยกว่าสามจุด
- ถ้าค่าเบี่ยงเบนมาตรฐานตัวอย่างเป็นศูนย์
รูปภาพด้านล่างแสดงวิธีใช้ฟังก์ชันเหล่านี้กับชุดข้อมูลเฉพาะของเรา:
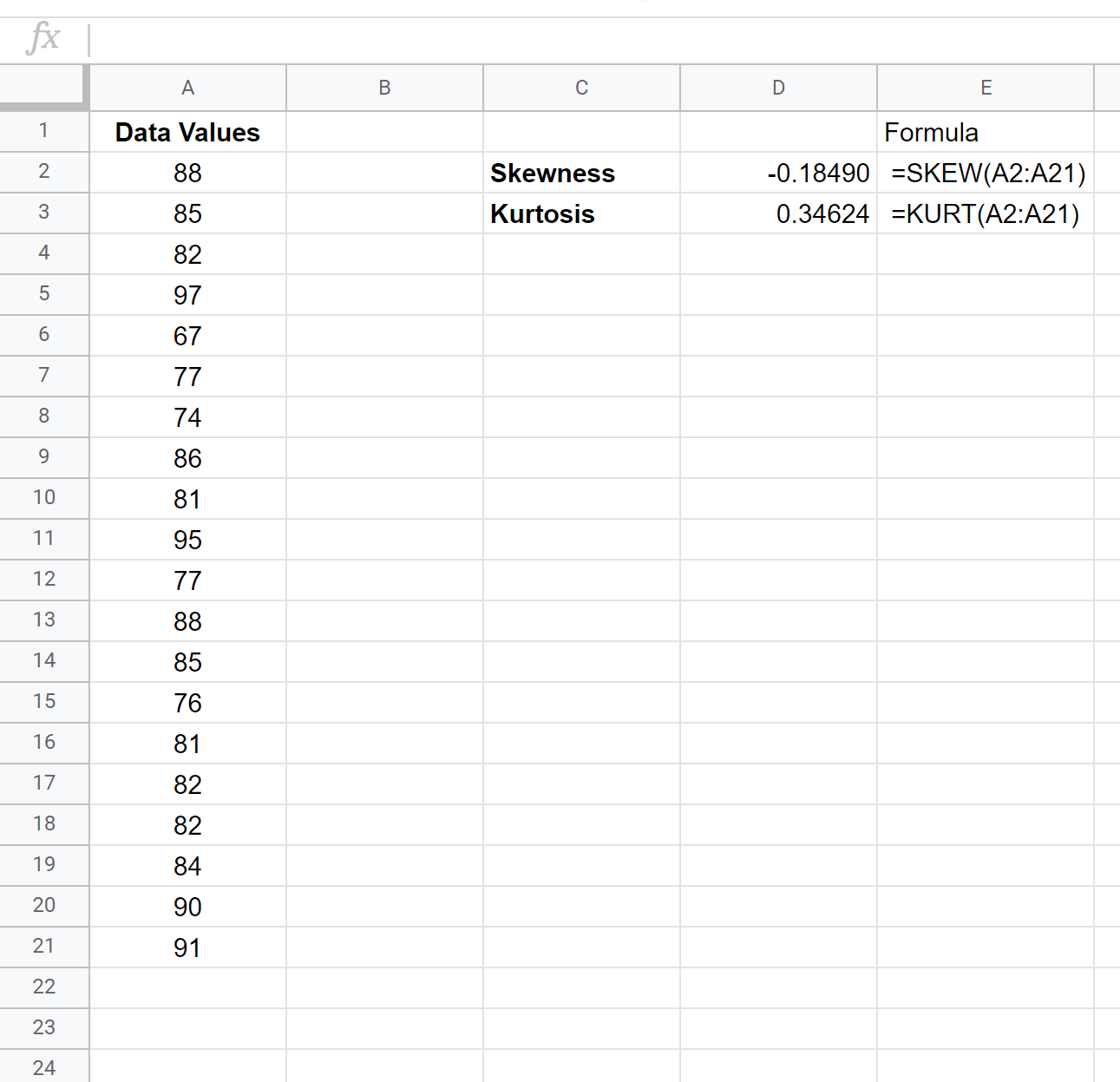
ความเบ้กลายเป็น -0.18490 และความโด่งกลายเป็น 0.34624 .
แหล่งข้อมูลเพิ่มเติม: เครื่องคำนวณความเบ้และเคอร์โทซิส
คุณยังสามารถคำนวณความเบ้สำหรับชุดข้อมูลที่กำหนดได้โดยใช้ เครื่องคำนวณความเบ้และความโด่งทางสถิติ ซึ่งจะคำนวณความเบ้และความโด่งสำหรับชุดข้อมูลที่กำหนดโดยอัตโนมัติ