วิธีสร้างเมทริกซ์สหสัมพันธ์ใน google ชีต

วิธีหนึ่งในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรสองตัวคือการใช้ สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ซึ่ง เป็นหน่วยวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว มีค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์จากศูนย์มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

แต่ในบางกรณี เราต้องการเข้าใจความสัมพันธ์ระหว่างตัวแปรหลายคู่ ในกรณีเหล่านี้ เราสามารถสร้าง เมทริกซ์สหสัมพันธ์ ซึ่งเป็นตารางสี่เหลี่ยมที่แสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างการผสมตัวแปรหลายคู่ตามลำดับ

บทแนะนำนี้จะอธิบายวิธีสร้างและตีความเมทริกซ์สหสัมพันธ์ใน Google ชีต

วิธีสร้างเมทริกซ์สหสัมพันธ์ใน Google ชีต

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงจำนวนแต้ม รีบาวน์ และแอสซิสต์โดยเฉลี่ยสำหรับผู้เล่นบาสเก็ตบอล 10 คน:

ในการสร้างเมทริกซ์สหสัมพันธ์สำหรับชุดข้อมูลนี้ เราสามารถใช้ฟังก์ชัน CORREL() กับไวยากรณ์ต่อไปนี้:

  COVAR(data_y, data_x)

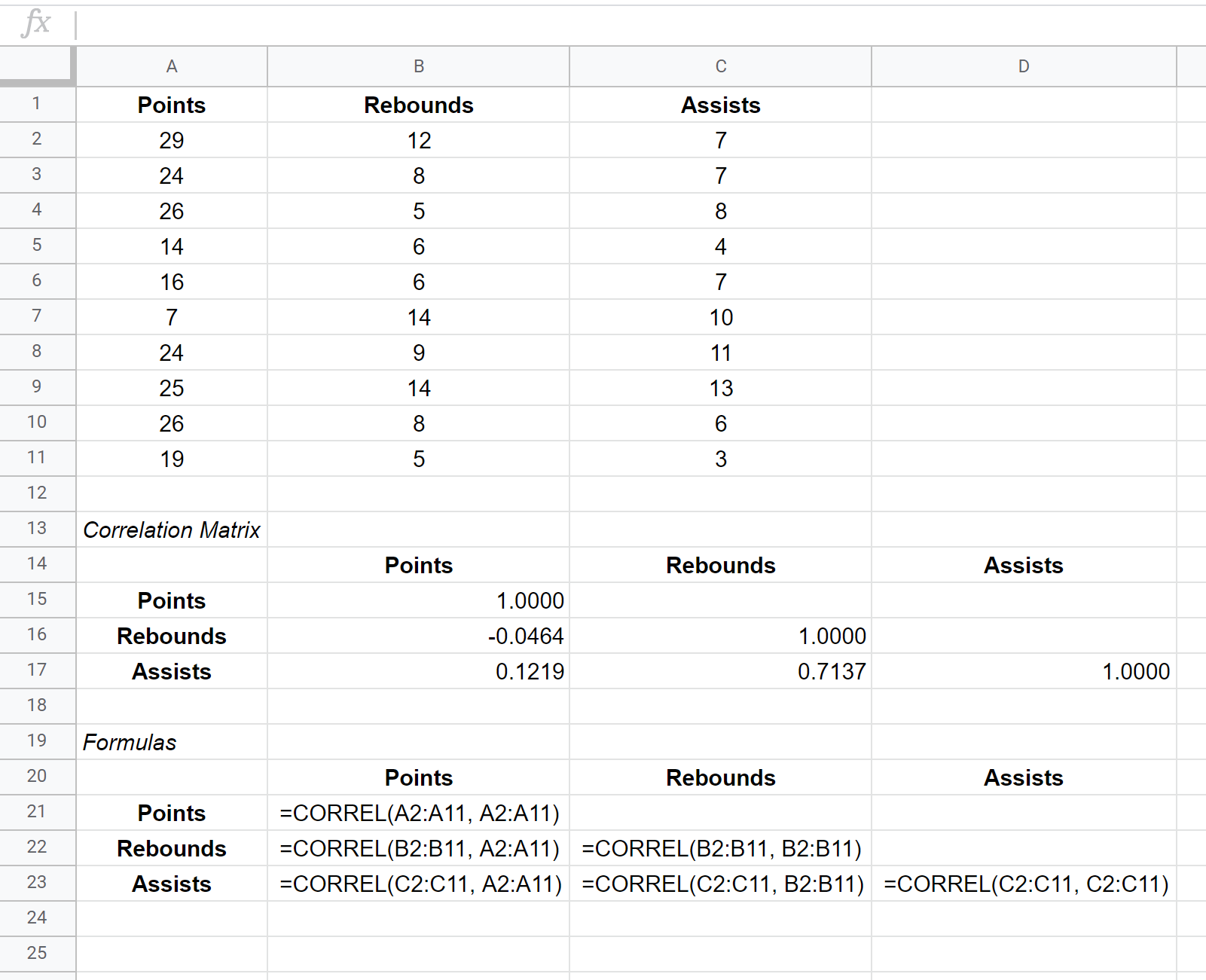
เมทริกซ์ความแปรปรวนร่วมสำหรับชุดข้อมูลนี้จะแสดงในเซลล์ B15:D17 ในขณะที่สูตรที่ใช้สร้างเมทริกซ์ความแปรปรวนร่วมจะแสดงในเซลล์ B21:D23 ด้านล่าง:

วิธีการตีความเมทริกซ์สหสัมพันธ์

ค่าในแต่ละเซลล์ของเมทริกซ์สหสัมพันธ์บอกเราถึงค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันระหว่างการรวมกันของตัวแปรแต่ละคู่ ตัวอย่างเช่น:

ความสัมพันธ์ระหว่างจุดและการรีบาวด์: -0.0464 คะแนนและการรีบาวด์มีความสัมพันธ์เชิงลบเล็กน้อย แต่ค่านี้ใกล้กับศูนย์มากจนไม่มีหลักฐานที่ชัดเจนของความสัมพันธ์ที่มีนัยสำคัญระหว่างตัวแปรทั้งสองนี้

สหสัมพันธ์ระหว่างแต้มกับแอสซิสต์: 0.1219 คะแนนและแอสซิสต์มีความสัมพันธ์เชิงบวกเล็กน้อย แต่ค่านี้ก็ค่อนข้างใกล้กับศูนย์เช่นกัน ดังนั้นจึงไม่มีหลักฐานที่ชัดเจนของความสัมพันธ์ที่มีนัยสำคัญระหว่างตัวแปรทั้งสองนี้

ความสัมพันธ์ระหว่างการรีบาวน์และแอสซิสต์: 0.7137 การรีบาวด์และแอสซิสต์มีความสัมพันธ์เชิงบวกอย่างมาก นั่นคือผู้เล่นที่มีการรีบาวด์มากกว่าก็มักจะได้รับแอสซิสต์มากกว่าเช่นกัน

โปรดทราบว่าค่าเส้นทแยงมุมของเมทริกซ์สหสัมพันธ์จะเป็น 1 ทั้งหมด เนื่องจากความสัมพันธ์ระหว่างตัวแปรกับตัวมันเองจะเป็น 1 เสมอ ในทางปฏิบัติ จำนวนนี้ไม่มีประโยชน์ในการตีความ

แหล่งข้อมูลเพิ่มเติม

วิธีอ่านเมทริกซ์สหสัมพันธ์
วิธีสร้างเมทริกซ์สหสัมพันธ์ใน Excel