รู้เบื้องต้นเกี่ยวกับการถดถอยสันเขา

ใน การถดถอยเชิงเส้นพหุคูณ แบบธรรมดา เราใช้ชุดของตัวแปรทำนาย p และ ตัวแปรตอบสนอง เพื่อให้พอดีกับแบบจำลองของรูปแบบ:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

ทอง:

• Y : ตัวแปรตอบสนอง
• X _j : ^{ตัวแปร} ทำนายที่ j
• β _j : ผลกระทบโดยเฉลี่ยต่อ Y ของการเพิ่มขึ้นของ X _j หนึ่งหน่วย โดยคงตัวทำนายอื่นๆ ทั้งหมดไว้คงที่
• ε : เงื่อนไขข้อผิดพลาด

ค่าของ β ₀ , β ₁ , B ₂ , …, β _p ถูกเลือกโดยใช้ วิธีกำลังสองน้อยที่สุด ซึ่งจะลดผลรวมของกำลังสองของส่วนที่เหลือ (RSS):

RSS = Σ(ฉัน _ฉัน – ŷ _ฉัน ) ²

ทอง:

• Σ : สัญลักษณ์กรีกหมายถึง ผลรวม
• y _i : ค่าตอบสนองจริงสำหรับการสังเกต ^{ครั้งที่ 3}
• ŷ _i : ค่าตอบสนองที่คาดการณ์ไว้ตามแบบจำลองการถดถอยเชิงเส้นพหุคูณ

อย่างไรก็ตาม เมื่อตัวแปรทำนายมีความสัมพันธ์กันสูง ความเป็นหลายคอลลิเนียร์ อาจกลายเป็นปัญหาได้ ซึ่งอาจทำให้การประมาณค่าสัมประสิทธิ์แบบจำลองไม่น่าเชื่อถือและแสดงความแปรปรวนสูง

วิธีหนึ่งในการแก้ไขปัญหานี้โดยไม่ต้องลบตัวแปรตัวทำนายบางตัวออกจากโมเดลโดยสิ้นเชิงคือการใช้วิธีการที่เรียกว่า Ridge Regression ซึ่งพยายามลดสิ่งต่อไปนี้ให้เหลือน้อยที่สุด

RSS + ΣΣβ _เจ ²

โดยที่ j ไปจาก 1 ถึง p และ แล ≥ 0

เทอมที่สองในสมการนี้เรียกว่า การลงโทษการถอน

เมื่อ แล = 0 เงื่อนไขการลงโทษนี้ไม่มีผลใดๆ และการถดถอยสันจะทำให้ค่าประมาณสัมประสิทธิ์เท่ากับกำลังสองน้อยที่สุด อย่างไรก็ตาม เมื่อ แล เข้าใกล้อนันต์ ค่าโทษจากการหดตัวจะมีอิทธิพลมากขึ้น และค่าสัมประสิทธิ์การถดถอยสูงสุดจะประมาณค่าเข้าใกล้ศูนย์

โดยทั่วไป ตัวแปรทำนายที่มีอิทธิพลน้อยที่สุดในแบบจำลองจะลดลงไปสู่ศูนย์เร็วที่สุด

เหตุใดจึงใช้ Ridge Regression

ข้อดีของการถดถอยแบบริดจ์เหนือการถดถอยกำลังสองน้อยที่สุดคือ การแลกเปลี่ยนระหว่างความแปรปรวนอคติ

โปรดจำไว้ว่า Mean Square Error (MSE) เป็นหน่วยเมตริกที่เราสามารถใช้เพื่อวัดความแม่นยำของแบบจำลองที่กำหนด และมีการคำนวณดังนี้

MSE = วาร์( f̂( x ₀ )) + [อคติ( f̂( x ₀ ))] ² + วาร์(ε)

MSE = ความแปรปรวน + อคติ ² + ข้อผิดพลาดที่ลดไม่ได้

แนวคิดพื้นฐานของการถดถอยริดจ์คือการแนะนำอคติเล็กน้อยเพื่อลดความแปรปรวนลงอย่างมาก ส่งผลให้ MSE โดยรวมลดลง

เพื่ออธิบายสิ่งนี้ ให้พิจารณากราฟต่อไปนี้:

โปรดทราบว่าเมื่อ แล เพิ่มขึ้น ความแปรปรวนจะลดลงอย่างมีนัยสำคัญโดยมีอคติเพิ่มขึ้นเล็กน้อย อย่างไรก็ตาม เมื่อเกินจุดใดจุดหนึ่ง ความแปรปรวนจะลดลงอย่างรวดเร็วน้อยลง และการลดลงของค่าสัมประสิทธิ์นำไปสู่การประเมินค่าเหล่านี้ต่ำเกินไปอย่างมีนัยสำคัญ ซึ่งนำไปสู่การเพิ่มขึ้นอย่างมากในอคติ

จากกราฟเราจะเห็นได้ว่า MSE ของการทดสอบนั้นต่ำที่สุด เมื่อเราเลือกค่าสำหรับ γ ที่สร้างการแลกเปลี่ยนที่เหมาะสมที่สุดระหว่างอคติและความแปรปรวน

เมื่อ แล = 0 เงื่อนไขการลงโทษในการถดถอยสันจะไม่มีผลใดๆ ดังนั้นจึงให้ค่าประมาณค่าสัมประสิทธิ์เดียวกันกับกำลังสองน้อยที่สุด อย่างไรก็ตาม การเพิ่ม แล ถึงจุดหนึ่งจะทำให้ค่า MSE โดยรวมของการทดสอบลดลงได้

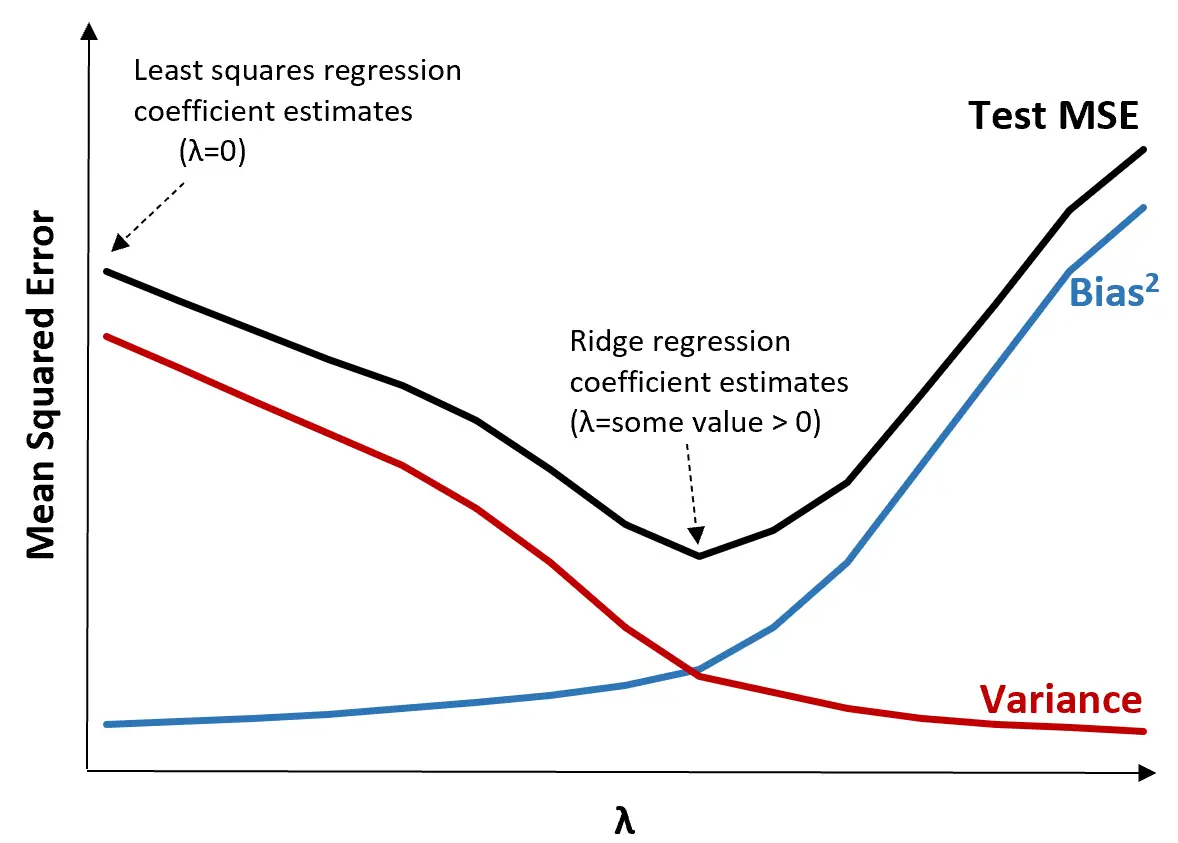
ซึ่งหมายความว่าการปรับโมเดลให้เหมาะสมโดยการถดถอยแบบสันจะทำให้เกิดข้อผิดพลาดในการทดสอบน้อยกว่าการปรับโมเดลให้เหมาะสมด้วยการถดถอยกำลังสองน้อยที่สุด

ขั้นตอนในการดำเนินการ Ridge Regression ในทางปฏิบัติ

ขั้นตอนต่อไปนี้สามารถใช้เพื่อดำเนินการถดถอยสัน:

ขั้นตอนที่ 1: คำนวณเมทริกซ์สหสัมพันธ์และค่า VIF สำหรับตัวแปรทำนาย

ขั้นแรก เราต้องสร้าง เมทริกซ์สหสัมพันธ์ และคำนวณ ค่า VIF (ปัจจัยอัตราเงินเฟ้อแปรปรวน) สำหรับตัวแปรทำนายแต่ละตัว

หากเราตรวจพบความสัมพันธ์ที่ชัดเจนระหว่างตัวแปรทำนายและค่า VIF สูง (ข้อความบางข้อความกำหนดค่า VIF “สูง” เป็น 5 ในขณะที่ข้อความอื่นๆ ใช้ 10) การถดถอยแบบสันเขาน่าจะเหมาะสม

อย่างไรก็ตาม หากข้อมูลไม่มีหลายคอลลิเนียริตี้ ก็อาจไม่จำเป็นต้องทำการถดถอยสันตั้งแต่แรก แต่เราสามารถใช้การถดถอยกำลังสองน้อยที่สุดแบบธรรมดาแทนได้

ขั้นตอนที่ 2: สร้างมาตรฐานให้กับตัวแปรทำนายแต่ละตัว

ก่อนดำเนินการการถดถอยแบบสันเขา เราจำเป็นต้องปรับขนาดข้อมูลเพื่อให้ตัวแปรตัวทำนายแต่ละตัวมีค่าเฉลี่ยเป็น 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1 เพื่อให้แน่ใจว่าไม่มีตัวแปรตัวทำนายตัวใดตัวหนึ่งที่มีอิทธิพลมากเกินไปเมื่อเรียกใช้การถดถอยแบบสันเขา

ขั้นตอนที่ 3: ปรับโมเดลการถดถอยสันเขาและเลือกค่าสำหรับ แล

ไม่มีสูตรที่แน่นอนที่เราสามารถใช้เพื่อกำหนดว่าจะใช้ค่าใดสำหรับ แล ในทางปฏิบัติ มีสองวิธีทั่วไปในการเลือก แล:

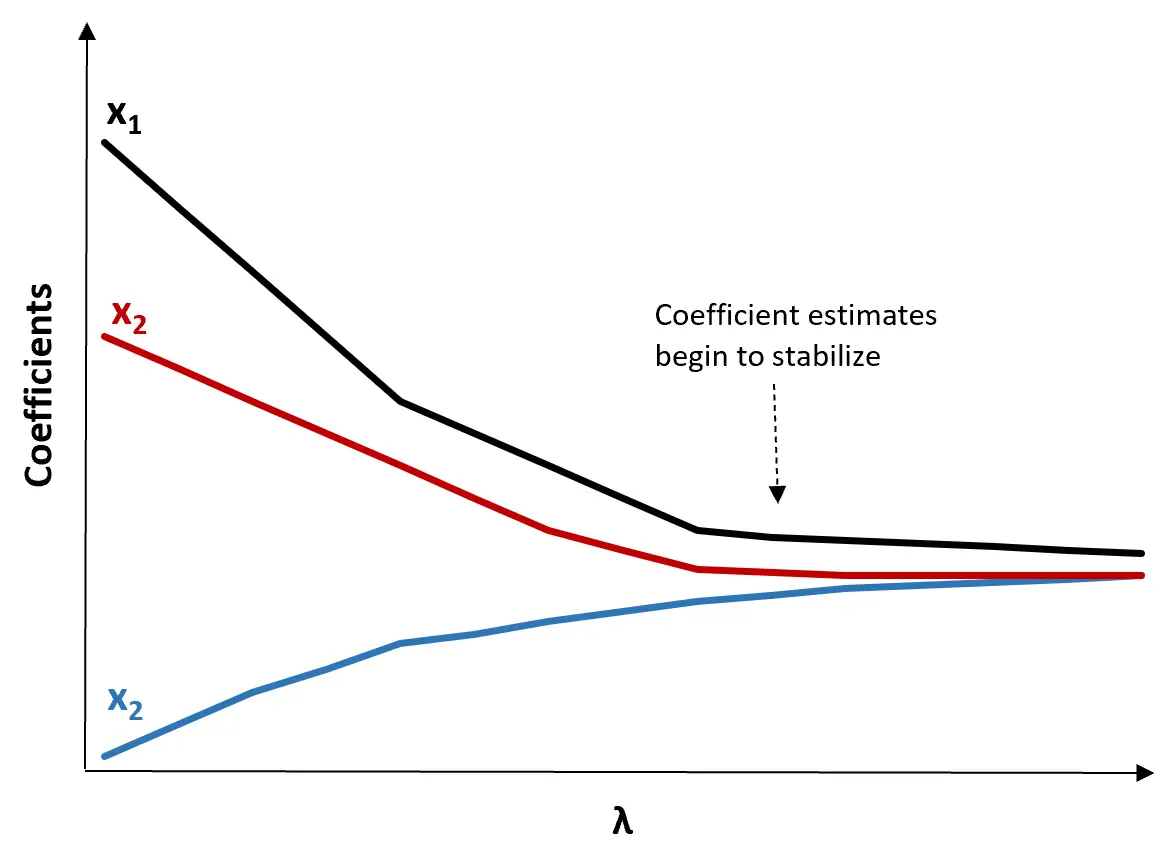
(1) สร้างพล็อตการติดตาม Ridge นี่คือกราฟที่แสดงภาพค่าของการประมาณค่าสัมประสิทธิ์เมื่อ แล เพิ่มขึ้นไปสู่อนันต์ โดยทั่วไป เราเลือก แล เป็นค่าที่การประมาณค่าสัมประสิทธิ์ส่วนใหญ่เริ่มมีเสถียรภาพ

(2) คำนวณการทดสอบ MSE สำหรับแต่ละค่าของ แล

อีกวิธีในการเลือก λ คือเพียงคำนวณ MSE ทดสอบของแต่ละรุ่นด้วยค่า แล ที่แตกต่างกัน และเลือก γ ให้เป็นค่าที่สร้าง MSE ทดสอบต่ำสุด

ข้อดีและข้อเสียของการถดถอยแบบสันเขา

ข้อได้เปรียบ ที่ใหญ่ที่สุดของการถดถอยแบบริดจ์คือความสามารถในการสร้างค่าความคลาดเคลื่อนกำลังสองเฉลี่ยในการทดสอบ (MSE) ที่ต่ำกว่ากำลังสองน้อยที่สุดเมื่อมีพหุคอลลิเนียร์

อย่างไรก็ตาม ข้อเสียเปรียบ ที่ใหญ่ที่สุดของการถดถอยแบบริดจ์คือการไม่สามารถทำการเลือกตัวแปรได้ เนื่องจากมีตัวแปรทำนายทั้งหมดในแบบจำลองสุดท้าย เนื่องจากตัวทำนายบางตัวจะลดลงจนใกล้ศูนย์มาก จึงอาจทำให้ตีความผลลัพธ์ของแบบจำลองได้ยาก

ในทางปฏิบัติ การถดถอยแบบริดจ์มีศักยภาพในการสร้างแบบจำลองที่สามารถคาดการณ์ได้ดีกว่าเมื่อเปรียบเทียบกับแบบจำลองกำลังสองน้อยที่สุด แต่มักจะตีความผลลัพธ์ของแบบจำลองได้ยากกว่า

ขึ้นอยู่กับว่าการตีความแบบจำลองหรือความแม่นยำในการคาดการณ์มีความสำคัญต่อคุณมากกว่าหรือไม่ คุณสามารถเลือกใช้กำลังสองน้อยที่สุดแบบธรรมดาหรือการถดถอยแบบสันในสถานการณ์ต่างๆ

การถดถอยริดจ์ใน R & Python

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการ ridge regression ใน R และ Python ซึ่งเป็นสองภาษาที่ใช้บ่อยที่สุดสำหรับการปรับโมเดล ridge regression ให้เหมาะสม:

Ridge Regression ใน R (ทีละขั้นตอน)
Ridge Regression ใน Python (ทีละขั้นตอน)