Lasso regression ใน r (ทีละขั้นตอน)
การถดถอยแบบ Lasso เป็นวิธีการที่เราสามารถใช้เพื่อให้พอดีกับแบบจำลองการถดถอยเมื่อมี multicollinearity ในข้อมูล
โดยสรุป การถดถอยกำลังสองน้อยที่สุดพยายามค้นหาการประมาณค่าสัมประสิทธิ์ที่ลดผลรวมที่เหลือของกำลังสอง (RSS):
RSS = Σ(ฉัน ฉัน – ŷ ฉัน )2
ทอง:
- Σ : สัญลักษณ์กรีกหมายถึง ผลรวม
- y i : ค่าตอบสนองจริงสำหรับการสังเกต ครั้งที่ 3
- ŷ i : ค่าตอบสนองที่คาดการณ์ไว้ตามแบบจำลองการถดถอยเชิงเส้นพหุคูณ
ในทางกลับกัน การถดถอยแบบ Lasso พยายามลดสิ่งต่อไปนี้ให้เหลือน้อยที่สุด:
RSS + ΣΣ|β j |
โดยที่ j ไปจาก 1 ถึง p ตัวแปรทำนายและ แล ≥ 0
เทอมที่สองในสมการนี้เรียกว่า การลงโทษการถอน ในการถดถอยแบบบ่วงบาศ เราเลือกค่าสำหรับ γ ที่สร้างการทดสอบ MSE (ข้อผิดพลาดกำลังสองเฉลี่ย) ต่ำที่สุดที่เป็นไปได้
บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีการถดถอยแบบบ่วงบาศใน R
ขั้นตอนที่ 1: โหลดข้อมูล
สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูลในตัวของ R ที่เรียกว่า mtcars เราจะใช้ hp เป็นตัวแปรตอบสนอง และตัวแปรต่อไปนี้เป็นตัวทำนาย:
- mpg
- น้ำหนัก
- อึ
- คิววินาที
เพื่อทำการถดถอยแบบบ่วงบาศ เราจะใช้ฟังก์ชันจากแพ็คเกจ glmnet แพคเกจนี้ต้องการให้ ตัวแปรตอบสนอง เป็นเวกเตอร์และชุดของตัวแปรทำนายต้องเป็นของคลาส data.matrix
รหัสต่อไปนี้แสดงวิธีกำหนดข้อมูลของเรา:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
ขั้นตอนที่ 2: ติดตั้งโมเดล Lasso Regression
ต่อไป เราจะใช้ฟังก์ชัน glmnet() เพื่อให้พอดีกับโมเดลการถดถอยแบบ Lasso และระบุ alpha=1
โปรดทราบว่าการตั้งค่าอัลฟ่าเท่ากับ 0 เทียบเท่ากับการใช้ การถดถอยสันเขา และการตั้งค่าอัลฟ่าเป็นค่าระหว่าง 0 ถึง 1 เทียบเท่ากับการใช้ตาข่ายแบบยืดหยุ่น
เพื่อพิจารณาว่าจะใช้ค่าใดสำหรับแลมบ์ดา เราจะดำเนิน การตรวจสอบข้าม k-fold และระบุค่าแลมบ์ดาที่ทำให้เกิดข้อผิดพลาดกำลังสองเฉลี่ยทดสอบต่ำที่สุด (MSE)
โปรดทราบว่าฟังก์ชัน cv.glmnet() จะทำการตรวจสอบข้าม k-fold โดยอัตโนมัติโดยใช้ k = 10 ครั้ง
library (glmnet)
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda
[1] 5.616345
#produce plot of test MSE by lambda value
plot(cv_model)
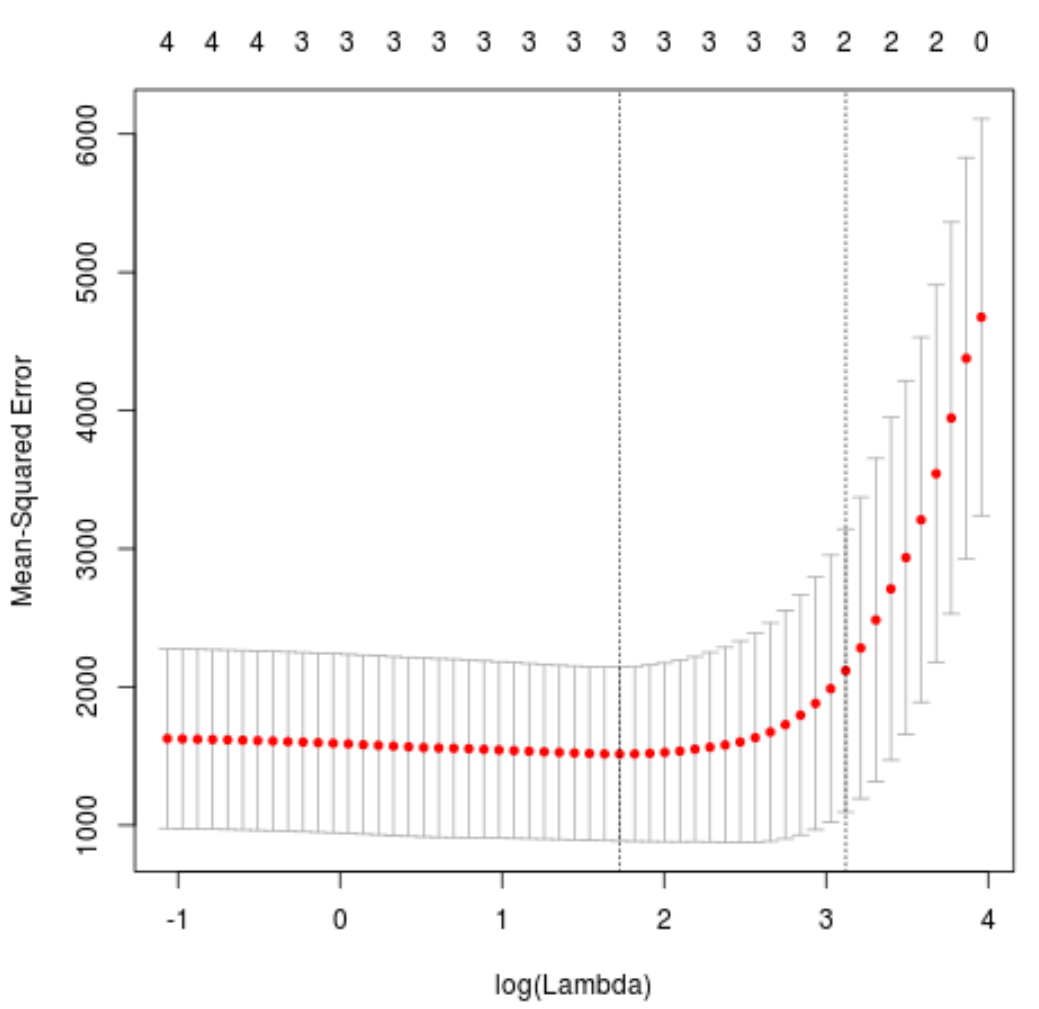
ค่าแลมบ์ดาที่ย่อการทดสอบ MSE ให้เหลือน้อยที่สุดกลายเป็น 5.616345
ขั้นตอนที่ 3: วิเคราะห์แบบจำลองขั้นสุดท้าย
สุดท้ายนี้ เราสามารถวิเคราะห์แบบจำลองสุดท้ายที่สร้างจากค่าแลมบ์ดาที่เหมาะสมที่สุดได้
เราสามารถใช้รหัสต่อไปนี้เพื่อรับการประมาณค่าสัมประสิทธิ์สำหรับแบบจำลองนี้:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.
qsec -19.43425
ไม่มีการแสดงค่าสัมประสิทธิ์สำหรับตัวทำนาย drat เนื่องจากการถดถอยแบบ Lasso ลดค่าสัมประสิทธิ์ให้เป็นศูนย์ ซึ่งหมายความว่าเขาถูกลบออกจากโมเดลโดยสิ้นเชิงเนื่องจากเขาไม่มีอิทธิพลเพียงพอ
โปรดทราบว่านี่เป็นข้อแตกต่างที่สำคัญระหว่าง การถดถอยแบบสัน และ การถดถอยแบบบ่วงบาศ การถดถอยแบบริดจ์จะลดค่าสัมประสิทธิ์ทั้งหมด ให้ เหลือศูนย์ แต่การถดถอยแบบบ่วงบาศมีศักยภาพในการลบตัวทำนายออกจากแบบจำลองโดยการลดค่าสัมประสิทธิ์ให้เหลือศูนย์ อย่างสมบูรณ์
นอกจากนี้เรายังสามารถใช้แบบจำลองการถดถอยแบบ Lasso สุดท้ายเพื่อคาดการณ์เกี่ยวกับการสังเกตใหม่ๆ ตัวอย่างเช่น สมมติว่าเรามีรถคันใหม่ที่มีคุณสมบัติดังต่อไปนี้:
- ไมล์ต่อแกลลอน: 24
- น้ำหนัก: 2.5
- ราคา: 3.5
- วินาที: 18.5
รหัสต่อไปนี้แสดงวิธีใช้แบบจำลองการถดถอยแบบบ่วงบาศเพื่อทำนายค่า hp ของการสังเกตใหม่นี้:
#define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 )
#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)
[1,] 109.0842
จากค่าที่ป้อน โมเดลคาดการณ์ว่ารถคันนี้จะมีค่า แรงม้า อยู่ที่ 109.0842 .
สุดท้ายนี้ เราสามารถคำนวณ R-squared ของโมเดล จากข้อมูลการฝึกได้:
#use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)
#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.8047064
R กำลังสองกลายเป็น 0.8047064 นั่นคือแบบจำลองที่ดีที่สุดสามารถอธิบายความแปรผันของค่าตอบสนองของข้อมูลการฝึกอบรม ได้ 80.47%
คุณสามารถค้นหาโค้ด R แบบเต็มที่ใช้ในตัวอย่างนี้ ได้ ที่นี่