การถดถอยเชิงเส้นพหุคูณด้วยมือ (ทีละขั้นตอน)
การถดถอยเชิงเส้นพหุคูณ เป็นวิธีการที่เราสามารถใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่สองตัวขึ้นไปกับ ตัวแปรตอบสนอง
บทช่วยสอนนี้จะอธิบายวิธีการถดถอยเชิงเส้นหลายรายการด้วยตนเอง
ตัวอย่าง: การถดถอยเชิงเส้นพหุคูณด้วยมือ
สมมติว่าเรามีชุดข้อมูลต่อไปนี้พร้อมตัวแปรตอบสนอง y และตัวแปรทำนายสองตัว x 1 และ x 2 :
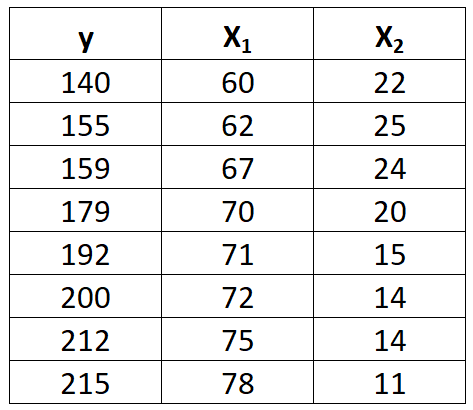
ทำตามขั้นตอนต่อไปนี้เพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นหลายตัวกับชุดข้อมูลนี้
ขั้นตอนที่ 1: คำนวณ x 1 2 , x 2 2 , x 1 y, x 2 y และ x 1 x 2
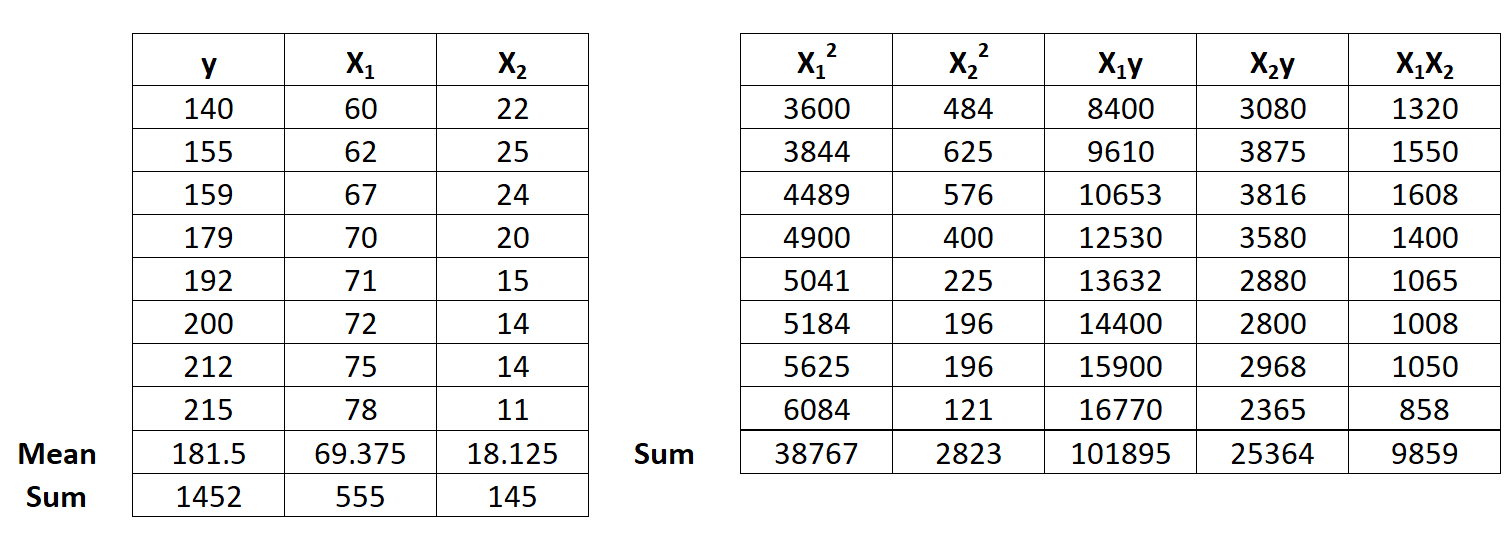
ขั้นตอนที่ 2: คำนวณผลรวมการถดถอย
จากนั้น ให้ดำเนินการคำนวณผลรวมการถดถอยต่อไปนี้:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38.767 – (555) 2 / 8 = 263.875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194.875
- Σ x 1 ปี = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
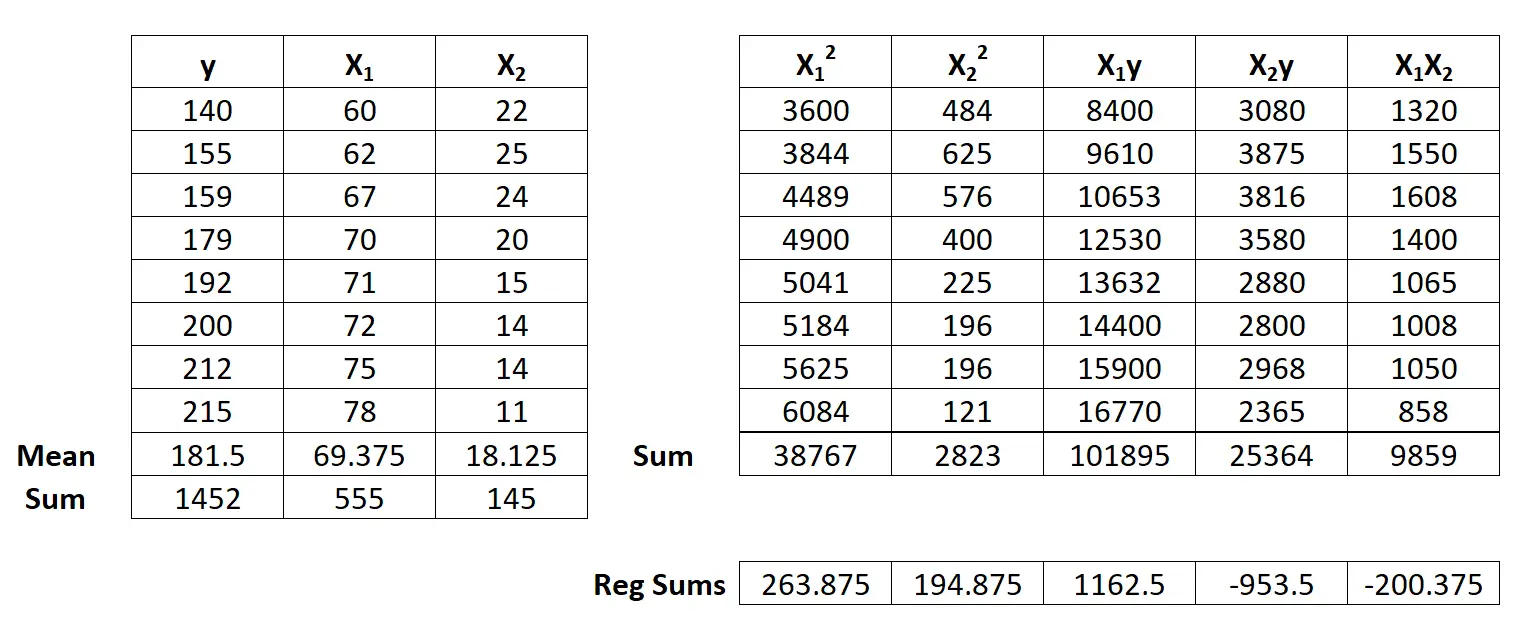
ขั้นตอนที่ 3: คำนวณ b 0 , b 1 และ b 2
สูตรคำนวณ b 1 คือ: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
ดังนั้น b 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
สูตรคำนวณ b 2 คือ: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
ดังนั้น b 2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375) 2 ] = -1.656
สูตรคำนวณ b 0 คือ: y – b 1 X 1 – b 2 X 2
ดังนั้น b 0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
ขั้นตอนที่ 5: วาง b 0 , b 1 และ b 2 ลงในสมการการถดถอยเชิงเส้นโดยประมาณ
สมการการถดถอยเชิงเส้นโดยประมาณคือ: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
ในตัวอย่างของเรา มันคือ ŷ = -6.867 + 3.148x 1 – 1.656x 2
วิธีการตีความสมการถดถอยเชิงเส้นพหุคูณ
ต่อไปนี้เป็นวิธีการตีความสมการการถดถอยเชิงเส้นโดยประมาณ: ŷ = -6.867 + 3.148x 1 – 1.656x 2
ข0 = -6.867 . เมื่อตัวแปรทำนายทั้งสองมีค่าเท่ากับศูนย์ ค่าเฉลี่ยของ y คือ -6.867
ข1 = 3.148 . การเพิ่มขึ้นของ x 1 หนึ่งหน่วยสัมพันธ์กับการเพิ่มขึ้นของ y โดยเฉลี่ย 3.148 หน่วย โดยสมมติว่า x 2 ยังคงคงที่
ข2 = -1.656 . การเพิ่มขึ้นหนึ่งหน่วยใน x 2 สัมพันธ์กับการลดลง 1,656 หน่วยใน y โดยเฉลี่ย โดยสมมติว่า x 1 ยังคงคงที่
แหล่งข้อมูลเพิ่มเติม
ความรู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นพหุคูณ
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายด้วยมือ
เกี่ยวกับผู้แต่ง
ดร.เบนจามิน แอนเดอร์สัน
สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม