การจำกัดขอบเขตคืออะไร?
บ่อยครั้งในสถิติเราพยายามวัด ความสัมพันธ์ ระหว่างตัวแปรสองตัว สิ่งนี้ช่วยให้เราเข้าใจสิ่งต่อไปนี้:
- ทิศทาง ความสัมพันธ์ระหว่างตัวแปรสองตัว เมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น ตัวแปรอีกตัวมีแนวโน้มเพิ่มขึ้นหรือลดลงหรือไม่?
- ความเข้มแข็ง ของความสัมพันธ์ระหว่างสองตัวแปร ค่าของตัวแปรทั้งสองจะเปลี่ยนไปเท่าใด?
น่าเสียดายที่ปัญหาที่อาจเกิดขึ้นเมื่อวัดความสัมพันธ์ระหว่างตัวแปรสองตัวเรียกว่า การจำกัดช่วง สิ่งนี้เกิดขึ้นเมื่อ ช่วง ของค่าที่วัดได้สำหรับตัวแปรตัวใดตัวหนึ่งถูกจำกัดด้วยเหตุผลบางประการ
ตัวอย่างเช่น สมมติว่าเราต้องการวัดความสัมพันธ์ระหว่าง ชั่วโมงเรียน กับ คะแนนสอบ ของนักเรียนในโรงเรียนแห่งใดแห่งหนึ่ง
หากเรารวบรวมข้อมูลตัวแปรทั้งสองนี้ให้กับนักเรียนทั้ง 1,000 คนในโรงเรียน เราอาจพบว่าความสัมพันธ์ระหว่าง ชั่วโมงเรียน กับ คะแนนสอบ คือ 0.73
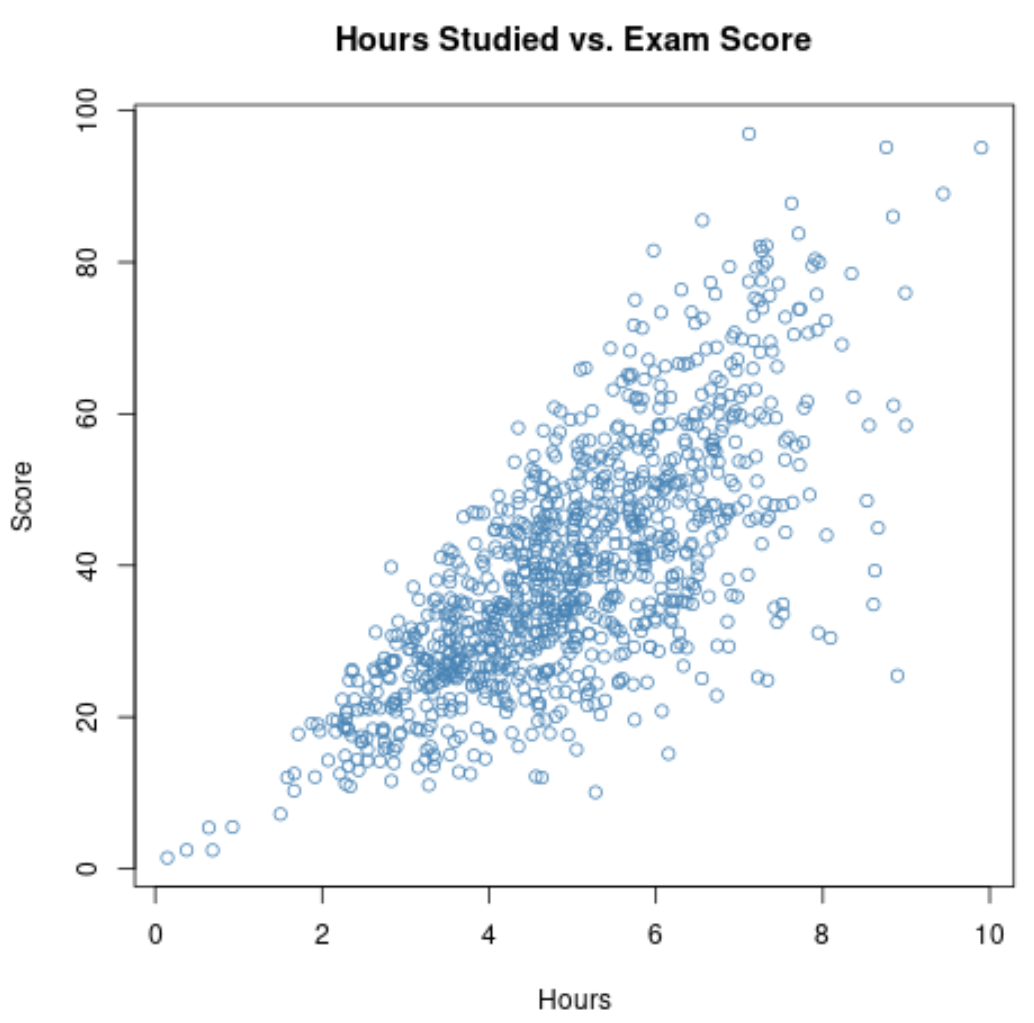
ความสัมพันธ์นี้ค่อนข้างสูง ซึ่งบ่งบอกถึงความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างตัวแปรทั้งสอง เมื่อนักเรียนเรียนมากขึ้น พวกเขามักจะทำข้อสอบได้ดีขึ้น
อย่างไรก็ตาม สมมติว่าเรารวบรวมข้อมูลของนักเรียนในหลักสูตรเกียรตินิยมเท่านั้น อาจเป็นไปได้ว่านักเรียนเหล่านี้เรียนมาแล้วอย่างน้อย 6 ชั่วโมง
ดังนั้น หากเราคำนวณความสัมพันธ์ระหว่าง ชั่วโมงเรียน กับ คะแนนสอบ ของนักเรียนเหล่านี้ เราจะใช้ช่วงแคบสำหรับ ชั่วโมงเรียนที่แปรผัน
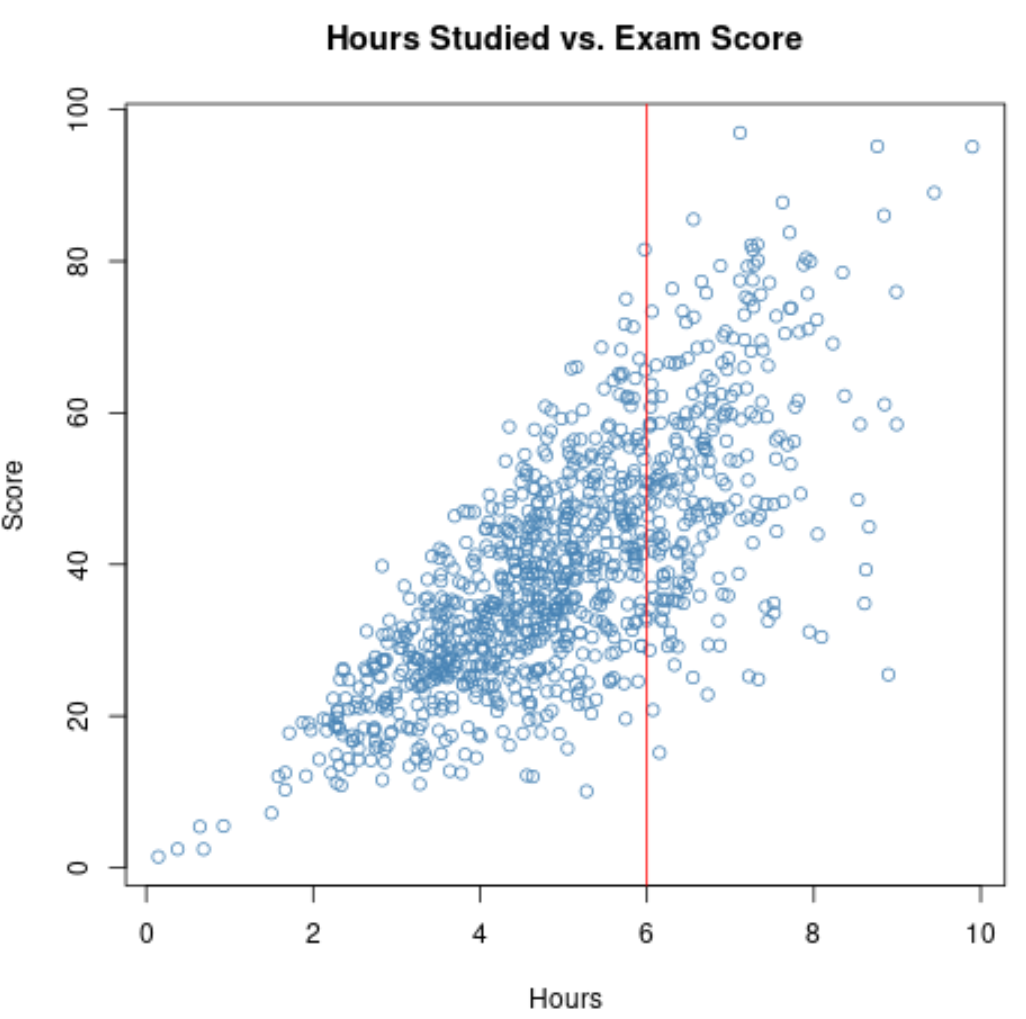
หากเราขยาย Scatterplot ในช่วงที่ ชั่วโมง มากกว่า 6 พล็อตจะมีลักษณะดังนี้:
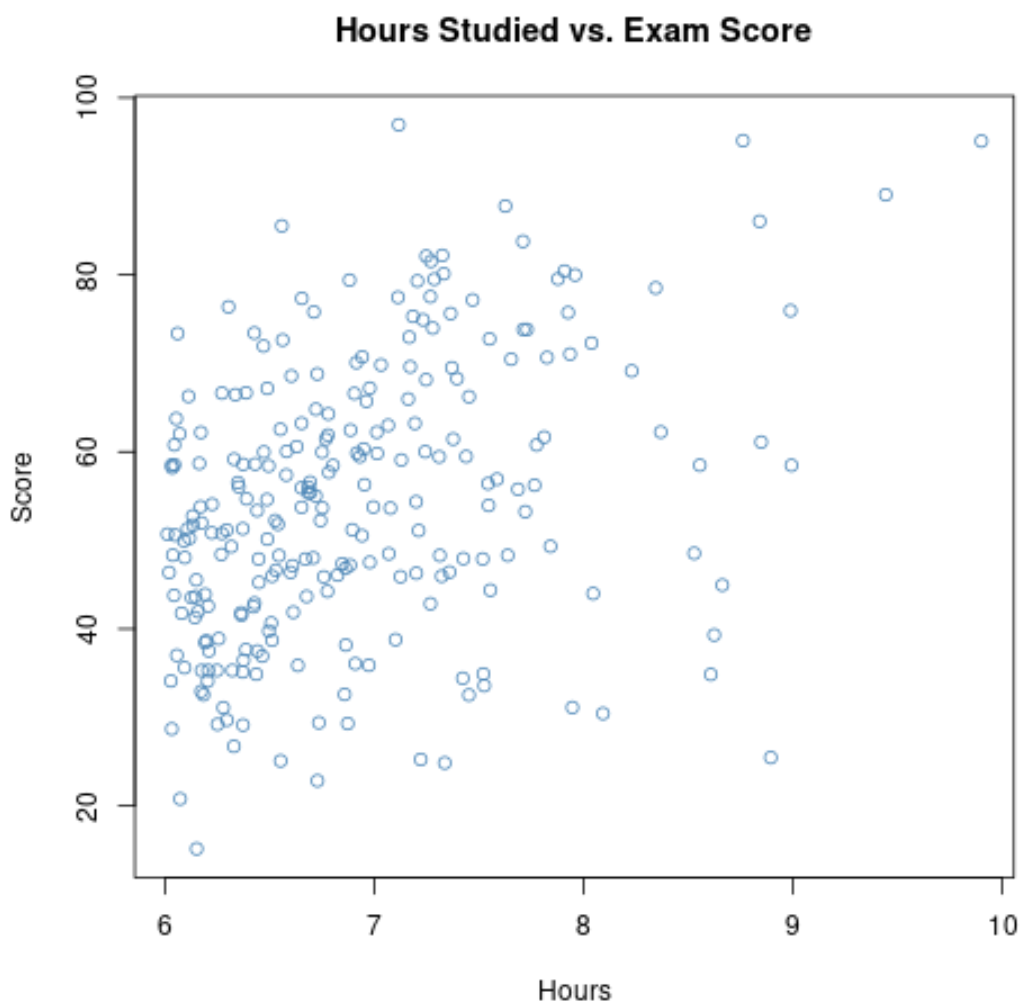
ความสัมพันธ์ระหว่างตัวแปรทั้งสองบนกราฟนี้กลายเป็น 0.37 ซึ่งต่ำกว่า 0.73 อย่างมีนัยสำคัญ
ดังนั้น หากเรารวบรวมข้อมูลเฉพาะ ชั่วโมงเรียน และ คะแนนสอบ ของนักเรียนในหลักสูตรเกียรตินิยม เราอาจถือว่ามีความสัมพันธ์ที่อ่อนแอระหว่างชั่วโมงเรียนกับคะแนนสอบ
อย่างไรก็ตาม ผลลัพธ์นี้อาจทำให้เข้าใจผิดเนื่องจากเราใช้ ช่วงที่จำกัด สำหรับตัวแปรตัวใดตัวหนึ่ง
ตัวอย่างช่วงที่จำกัดในโลกแห่งความเป็นจริง
ปัญหาของช่วงที่จำกัดสามารถเกิดขึ้นได้ในทางปฏิบัติในการศึกษาวิจัยต่างๆ มากมาย นี่คือตัวอย่างบางส่วน:
1. การศึกษานักกีฬาที่มีสมรรถนะสูง นักวิจัยอาจสนใจที่จะศึกษาว่าโปรแกรมการฝึกบางโปรแกรมสร้างมวลกล้ามเนื้อมากกว่าโปรแกรมมาตรฐานบางโปรแกรมหรือไม่
หากนักวิจัยรวบรวมข้อมูลเฉพาะนักกีฬาชั้นนำ ก็มีแนวโน้มว่านักกีฬาเหล่านี้ล้วนมีมวลกล้ามเนื้อสูงอยู่แล้ว จึงจะมีช่วงค่าที่แคบในการคำนวณความสัมพันธ์ระหว่างโปรแกรมการฝึกกับมวลกล้ามเนื้อที่ผลิตได้
2. การศึกษาของนักเรียนที่มีผลสัมฤทธิ์สูง นักวิจัยอาจต้องการศึกษาว่าโปรแกรมการสอนบางหลักสูตรมีผลดีต่อเกรดหรือไม่ โดยธรรมชาติแล้ว นักเรียนที่กระตือรือร้นที่จะปรับปรุงผลการเรียนของตนเองและเข้าร่วมในโครงการกวดวิชาอาจเป็นนักเรียนที่มีผลการเรียนดีอยู่แล้ว
ดังนั้นคะแนนของนักเรียนเหล่านี้อาจพัฒนาได้ไม่มากนัก เมื่อผู้วิจัยคำนวณความสัมพันธ์ระหว่างชั่วโมงที่ใช้ในโปรแกรมการสอนและผลการเพิ่มเกรด ความสัมพันธ์ที่แท้จริงอาจถูกประเมินต่ำเกินไป เนื่องจากพื้นที่สำหรับการปรับปรุงเกรดถูกจำกัด
วิธีพิจารณาถึงช่วงที่จำกัด
วิธียอดนิยมในการคำนึงถึงช่วงที่จำกัดเรียกว่า Thorndike Case 2 ซึ่งเป็นสูตรที่พัฒนาโดยนักจิตวิทยา Robert L. Thorndike
สูตรนี้ให้ค่าประมาณความสัมพันธ์ที่แท้จริงระหว่างตัวแปรสองตัวและใช้การคำนวณต่อไปนี้:
ความสัมพันธ์ที่แท้จริง = √(1-(SD 2 y จำกัด -SD 2 y ไม่ จำกัด )) * (1-r 2 จำกัด )
ทอง:
- SD 2 ถูกจำกัด y : ค่าเบี่ยงเบนมาตรฐานกำลังสองของข้อมูลที่มีอยู่ในตัวแปรตอบสนอง y
- SD 2 ไม่จำกัด : ค่าเบี่ยงเบนมาตรฐานกำลังสองที่ทราบของตัวแปรตอบสนองสำหรับประชากร
- r 2 ถูกจำกัด : ความสัมพันธ์กำลังสองกับข้อมูลที่ถูกจำกัดที่มีอยู่
สูตรนี้แสดงให้เห็นว่ามีประสิทธิผลในการสร้างค่าประมาณความสัมพันธ์ที่แท้จริงระหว่างตัวแปรสองตัวที่เป็นกลางเมื่อตัวแปรตัวใดตัวหนึ่งทนทุกข์ทรมานจากช่วงที่จำกัด
โปรดทราบว่าในการใช้สูตรนี้ คุณต้องมีค่าประมาณของค่าเบี่ยงเบนมาตรฐานประชากรที่แท้จริงสำหรับตัวแปรตอบสนอง