คำอธิบายง่ายๆ เกี่ยวกับความถูกต้องของเกณฑ์

ความถูกต้องตามเกณฑ์ หมายถึงความสามารถในการวัดตัวแปรหนึ่งเพื่อทำนายการตอบสนองของตัวแปรอีกตัวหนึ่ง

ตัวแปรหนึ่งเรียกว่า ตัวแปรอธิบาย ในขณะที่ตัวแปรอื่นเรียกว่า ตัวแปรเกณฑ์

ตัวอย่างเช่น เราอาจต้องการทราบว่าการสอบเข้าวิทยาลัยบางประเภทสามารถทำนายคะแนนเฉลี่ยเกรดเฉลี่ยภาคเรียนแรกของนักเรียนได้ดีเพียงใด

การสอบเข้าจะเป็นตัวแปรอธิบายและตัวแปรเกณฑ์จะเป็นเกรดเฉลี่ยภาคการศึกษาแรก

เราต้องการทราบว่าการใช้ตัวแปรอธิบายเฉพาะนี้เป็นวิธีการทำนายตัวแปรเกณฑ์นั้น ถูกต้องหรือไม่

วิธีวัดความถูกต้องของเกณฑ์

โดยทั่วไป เราจะวัดความถูกต้องของเกณฑ์โดยใช้หน่วยเมตริก เช่น ค่าสัมประสิทธิ์สหสัมพันธ์ของ Pearson ซึ่งรับค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์จากศูนย์มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

เช่น ถ้าเรารวบรวมข้อมูลคะแนนสอบเข้าและเกรดเฉลี่ยภาคเรียนแรกจำนวน 1,000 คน และพบว่าตัวแปรทั้งสองมีความสัมพันธ์กันเท่ากับ 0.843 แสดงว่าตัวแปรทั้งสองมีความสัมพันธ์กันสูง

กล่าวอีกนัยหนึ่ง นักเรียนที่ได้คะแนนสูงในการสอบเข้าก็มีแนวโน้มที่จะได้คะแนนสูงในภาคการศึกษาแรกเช่นกัน ในทางกลับกัน นักเรียนที่ได้คะแนนสอบเข้าต่ำมักจะมีเกรดเฉลี่ยต่ำในช่วงภาคการศึกษาแรก

ประเภทของความถูกต้องของเกณฑ์

ความถูกต้องของเกณฑ์มีสองประเภทหลัก:

1. ความถูกต้องเชิงคาดการณ์

ความถูกต้องของเกณฑ์ประเภทแรกเรียกว่าความถูกต้องเชิงคาดการณ์ ซึ่งกำหนดว่าการวัดตัวแปรสามารถทำนายการวัดตัวแปรในอนาคตได้อย่างแม่นยำหรือไม่

ตัวอย่างก่อนหน้านี้ของการวัดคะแนนสอบเข้าวิทยาลัยของนักเรียนและเกรดเฉลี่ยภาคการศึกษาแรกคือตัวอย่างของการวัดความถูกต้องเชิงคาดการณ์ เนื่องจากเรากำลังวัดตัวแปรสองตัวในเวลาที่ต่างกัน

กล่าวอีกนัยหนึ่งคือเราพยายามพิจารณาว่าคะแนนสอบเข้าสามารถ ทำนาย เกรดเฉลี่ยภาคการศึกษาแรกได้ดีหรือไม่

2. ความถูกต้องพร้อมกัน

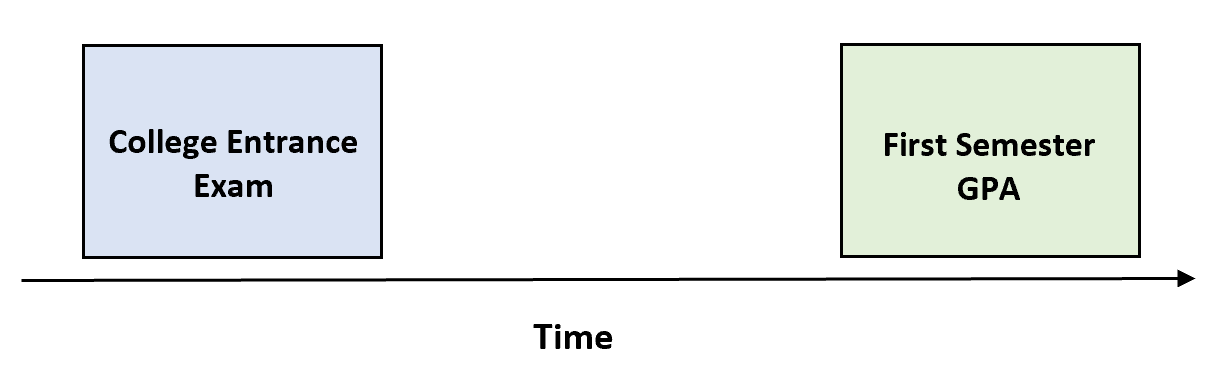
ความถูกต้องของเกณฑ์ประเภทที่สองเรียกว่าความถูกต้องที่เกิดขึ้นพร้อมกัน ซึ่งวัดตัวแปรสองตัว พร้อมกัน (เช่น ในเวลาเดียวกัน) เพื่อดูว่าตัวแปรตัวหนึ่งมีความเกี่ยวข้องอย่างมีนัยสำคัญกับอีกตัวหนึ่งหรือไม่

ตัวอย่างนี้คือหากบริษัทจัดการทดสอบบางประเภทเพื่อดูว่าผลการทดสอบมีความสัมพันธ์กับประสิทธิภาพการทำงานของพนักงานหรือไม่

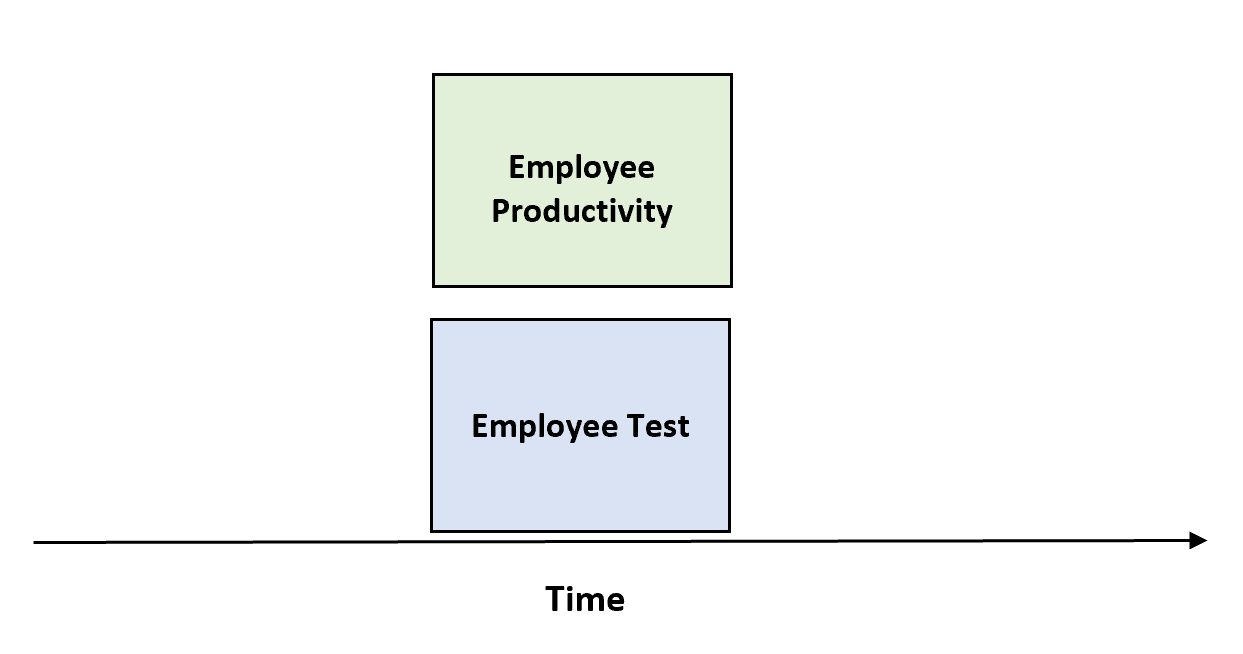
ข้อดีของแนวทางนี้คือเราไม่จำเป็นต้องรอเวลาในอนาคตเพื่อทำการวัดเกณฑ์ตัวแปรที่น่าสนใจ