เหตุการณ์ที่ครบถ้วนสมบูรณ์: คำจำกัดความและตัวอย่าง
ชุดของเหตุการณ์จะ ครอบคลุมทั้งหมด หาก คาด ว่าจะเกิดเหตุการณ์อย่างน้อยหนึ่งเหตุการณ์
ตัวอย่างเช่น ถ้าเราทอยลูกเต๋า มันจะต้องตกลงไปที่ค่าใดค่าหนึ่งต่อไปนี้:
- 1
- 2
- 3
- 4
- 5
- 6
ดังนั้น เราจะบอกว่าเซตของเหตุการณ์ {1, 2, 3, 4, 5, 6} นั้น ครบถ้วนสมบูรณ์ เพราะการตาย จะต้อง ตกลงบนค่าใดค่าหนึ่งเหล่านี้
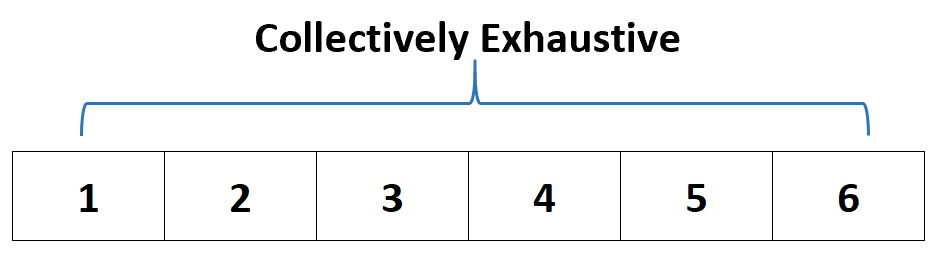
กล่าวอีกนัยหนึ่ง ชุดของเหตุการณ์นี้ในฐานะ คอลเลกชัน จะทำให้ผลลัพธ์ที่เป็นไปได้ทั้งหมด หมดลง
ตัวอย่างต่อไปนี้แสดงสถานการณ์อื่นๆ ที่แสดงให้เห็นถึงเหตุการณ์ที่ครบถ้วนสมบูรณ์:
ตัวอย่างที่ 1: พลิกเหรียญ
สมมติว่าเราโยนเหรียญหนึ่งครั้ง เรารู้ว่าเหรียญจะต้องตกลงบนค่าใดค่าหนึ่งต่อไปนี้:
- หัว
- ก้อย
ดังนั้น ชุดของเหตุการณ์ {Head, Tail} คงจะครบถ้วนสมบูรณ์
ตัวอย่างที่ 2: การหมุนด้านบน
สมมติว่าเรามีวงล้อรูเล็ตที่มีสามสีที่แตกต่างกัน: แดง น้ำเงิน และเขียว
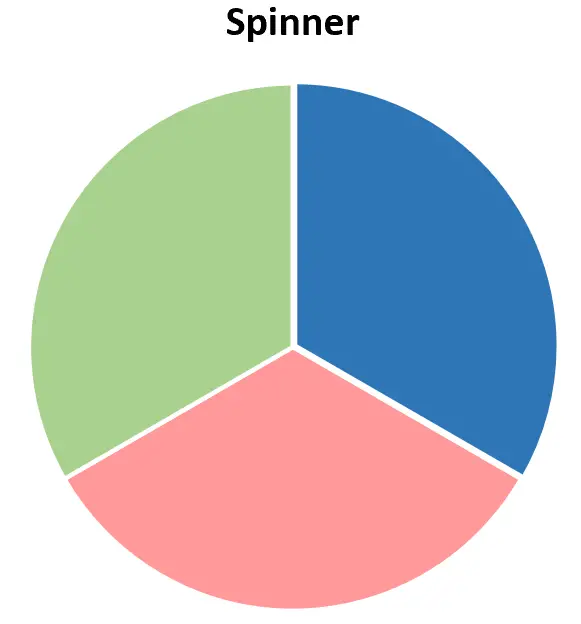
หากเราหมุนมันหนึ่งครั้ง มันควรจะตกลงไปที่ค่าใดค่าหนึ่งต่อไปนี้:
- สีแดง
- สีฟ้า
- สีเขียว
ดังนั้น ชุดของเหตุการณ์ {แดง น้ำเงิน เขียว} คงจะครบถ้วนสมบูรณ์
อย่างไรก็ตาม ชุดของเหตุการณ์ {Red, Green} จะ ไม่ ได้รวบรวมไว้ทั้งหมด เนื่องจากไม่ได้มีผลลัพธ์ที่เป็นไปได้ทั้งหมด
ตัวอย่างที่ 3: ประเภทของผู้เล่นบาสเก็ตบอล
สมมติว่าเรามีแบบสำรวจที่ขอให้บุคคลเลือกตำแหน่งบาสเก็ตบอลที่ต้องการ คำตอบเดียวที่เป็นไปได้คือ:
- ผู้นำเกม
- ยามยิง
- เล็กข้าง
- พลังไปข้างหน้า
- ศูนย์
ดังนั้นชุดของเหตุการณ์ {Point Guard, Shooting Guard, Small Forward, Power Forward, Center} จะครบถ้วนสมบูรณ์
อย่างไรก็ตาม ชุดของเหตุการณ์ {Point Guard, Shooting Guard, Small Forward} จะ ไม่ ครอบคลุมทั้งหมด เนื่องจากไม่ได้มีผลลัพธ์ที่เป็นไปได้ทั้งหมด
ความสำคัญของเหตุการณ์ที่ครบถ้วนสมบูรณ์ในการสำรวจ
เมื่อออกแบบแบบสำรวจ สิ่งสำคัญอย่างยิ่งคือคำตอบของคำถามจะต้องครอบคลุมโดยรวม
ตัวอย่างเช่น สมมติว่าแบบสำรวจถามคำถามต่อไปนี้:
ตำแหน่งบาสเก็ตบอลที่คุณชื่นชอบคืออะไร?
และสมมติว่าคำตอบที่เป็นไปได้คือ:
- ผู้นำเกม
- ยามยิง
- เล็กข้าง
- พลังไปข้างหน้า
ตำแหน่ง ศูนย์กลาง ถูกละทิ้งไป คำตอบเหล่านี้ไม่ได้รวบรวมไว้ทั้งหมด
ซึ่งหมายความว่าผู้ที่ชอบ Center เป็นตำแหน่งที่ต้องการจะต้องเลือกหนึ่งในตัวเลือกอื่น ซึ่งหมายความว่าการตอบแบบสำรวจจะไม่สะท้อนความคิดเห็นที่แท้จริงของผู้ตอบแบบสำรวจ
ครบถ้วนสมบูรณ์หรือแยกออกจากกัน
เหตุการณ์จะแยก จากกัน หากไม่สามารถเกิดขึ้นพร้อมกันได้
ตัวอย่างเช่น ให้เหตุการณ์ A เป็นเหตุการณ์ที่ผู้ตายตกลงบนเลขคู่ และให้เหตุการณ์ B เป็นเหตุการณ์ที่ผู้ตายตกลงบนเลขคี่
เราจะกำหนด พื้นที่ตัวอย่าง สำหรับกิจกรรมดังนี้:
- ก = {2, 4, 6}
- ข = {1, 3, 5}
โปรดทราบว่าไม่มีการทับซ้อนกันระหว่างช่องว่างสองช่องตัวอย่าง ซึ่งหมายความว่าช่องทั้งสองช่องแยกจากกัน พวกมันยังเกิดขึ้นได้อย่างละเอียดถี่ถ้วนโดยรวมเพราะเมื่อรวมกันแล้วพวกมันสามารถคำนึงถึงผลลัพธ์ที่เป็นไปได้ทั้งหมดของการหมุนแบบตายตัว
อย่างไรก็ตาม สมมติว่าเรากำหนดเหตุการณ์ A และเหตุการณ์ B ดังนี้
- ก = {1, 2, 3, 4}
- ข = {3, 4, 5, 6}
ในกรณีนี้ มีการทับซ้อนกันระหว่าง A และ B ดังนั้นจึงไม่ได้แยกจากกัน อย่างไรก็ตาม เมื่อรวมกันแล้ว พวกเขายังคงสามารถคำนึงถึงผลลัพธ์ที่เป็นไปได้ทั้งหมดของการหมุนแม่พิมพ์ได้
สิ่งนี้แสดงให้เห็นถึงจุดสำคัญ: ชุดของเหตุการณ์สามารถสรุปได้ครบถ้วนโดยไม่ต้องแยกจากกัน