วิธีใช้ตัวแปรจำลองในการวิเคราะห์การถดถอย

การถดถอยเชิงเส้น เป็นวิธีการที่เราสามารถใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่หนึ่งตัวขึ้นไปกับ ตัวแปรตอบสนอง

โดยทั่วไปเราใช้การถดถอยเชิงเส้นกับ ตัวแปรเชิงปริมาณ บางครั้งเรียกว่าตัวแปร “ตัวเลข” ซึ่งเป็นตัวแปรที่แสดงถึงปริมาณที่วัดได้ ตัวอย่างได้แก่:

• จำนวนตารางฟุตในบ้าน
• ขนาดประชากรของเมือง
• อายุของแต่ละบุคคล

อย่างไรก็ตาม บางครั้งเราต้องการใช้ตัวแปรเชิงหมวดหมู่เป็นตัวแปรทำนาย เหล่านี้เป็นตัวแปรที่ใช้ชื่อหรือป้ายกำกับและสามารถจัดเป็นหมวดหมู่ได้ ตัวอย่างได้แก่:

• สีตา (เช่น “สีฟ้า”, “สีเขียว”, “สีน้ำตาล”)
• เพศ (เช่น “ผู้ชาย” “ผู้หญิง”)
• สถานภาพการสมรส (เช่น “แต่งงานแล้ว” “โสด” “หย่าร้าง”)

เมื่อใช้ตัวแปรเด็ดขาด มันไม่สมเหตุสมผลเลยที่จะกำหนดค่าเช่น 1, 2, 3 ให้กับค่าเช่น “สีน้ำเงิน”, “สีเขียว” และ “สีน้ำตาล” เพราะมันไม่เหมาะสมที่จะพูด สีเขียวนั้นเป็นสองเท่า สีสันอย่างสีน้ำเงินหรือสีน้ำตาลก็มีสีสันมากกว่าสีน้ำเงินถึงสามเท่า

วิธีแก้ไขคือใช้ ตัวแปรจำลองแทน ตัวแปรเหล่านี้เป็นตัวแปรที่เราสร้างขึ้นโดยเฉพาะสำหรับการวิเคราะห์การถดถอย และใช้ค่าใดค่าหนึ่งจากสองค่า: ศูนย์หรือหนึ่งค่า

ตัวแปรจำลอง: ตัวแปรตัวเลขที่ใช้ในการวิเคราะห์การถดถอยเพื่อแสดงข้อมูลเชิงหมวดหมู่ที่สามารถรับได้เพียงค่าใดค่าหนึ่งจากสองค่าเท่านั้น: ศูนย์หรือหนึ่งค่า

จำนวนตัวแปรจำลองที่เราต้องสร้างมีค่าเท่ากับ k -1 โดยที่ k คือจำนวนค่าต่างๆ ที่ตัวแปรหมวดหมู่สามารถรับได้

ตัวอย่างต่อไปนี้แสดงวิธีสร้างตัวแปรจำลองสำหรับชุดข้อมูลต่างๆ

ตัวอย่างที่ 1: สร้างตัวแปรจำลองโดยมีค่าเพียงสองค่าเท่านั้น

สมมติว่าเรามีชุดข้อมูลต่อไปนี้และต้องการใช้ เพศ และ อายุ เพื่อทำนาย รายได้ :

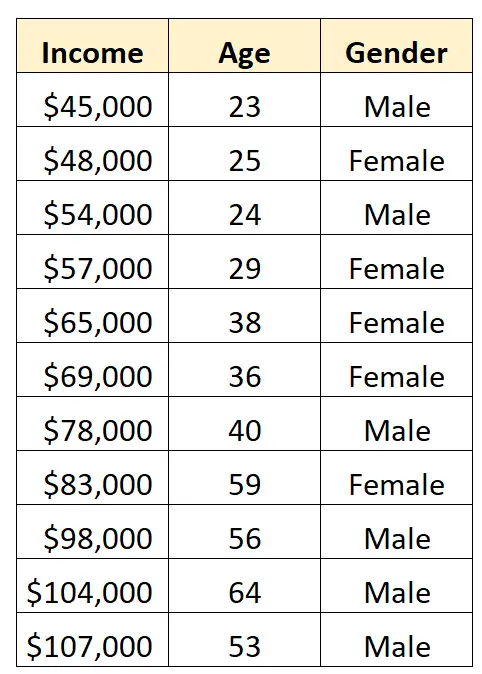
หากต้องการใช้ เพศ เป็นตัวแปรทำนายในแบบจำลองการถดถอย เราจำเป็นต้องแปลงให้เป็นตัวแปรจำลอง

เนื่องจากปัจจุบันนี้เป็นตัวแปรเด็ดขาดที่สามารถรับค่าที่แตกต่างกันได้สองค่า (“ชาย” หรือ “หญิง”) เราเพียงสร้างตัวแปรจำลอง k -1 = 2-1 = 1 ตัว

ในการสร้างตัวแปรจำลองนี้ เราสามารถเลือกค่าใดค่าหนึ่ง (“ชาย” หรือ “หญิง”) เพื่อแทน 0 และอีกค่าหนึ่งแทน 1

โดยทั่วไป เรามักจะแสดงค่าที่พบบ่อยที่สุดด้วย 0 ซึ่งจะเป็น “Male” ในชุดข้อมูลนี้

ต่อไปนี้เป็นวิธีแปลง เพศ ให้เป็นตัวแปรจำลอง:

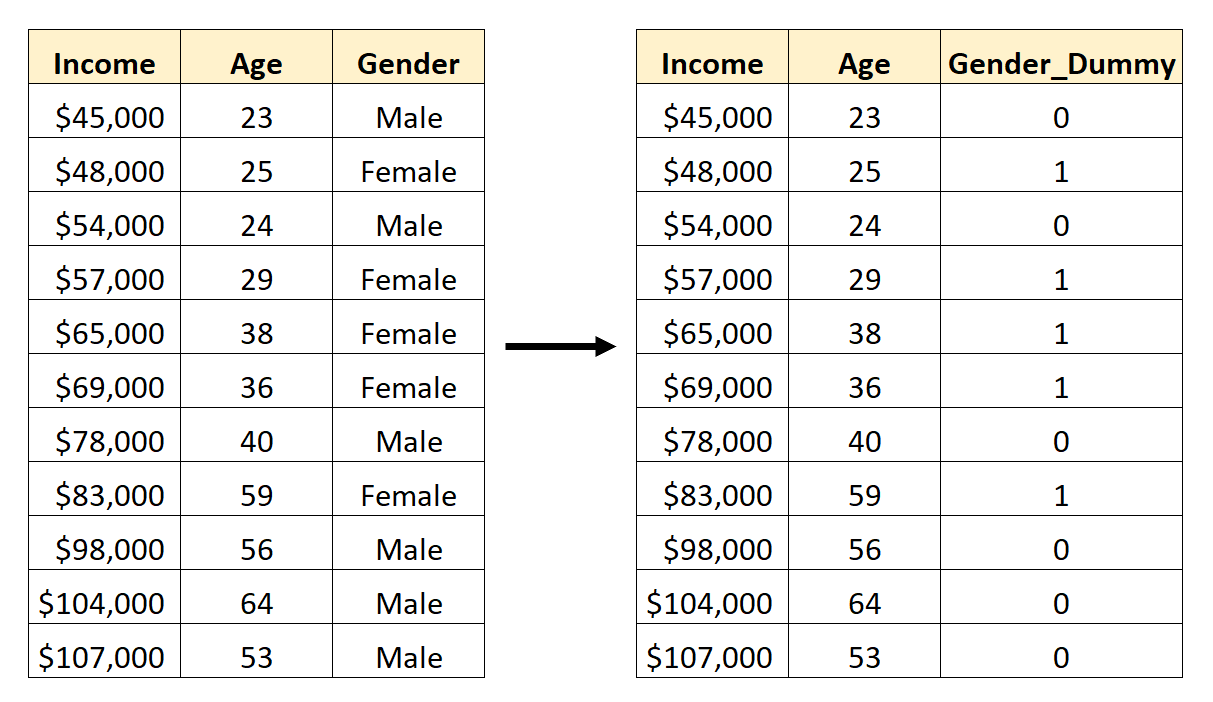
จากนั้นเราสามารถใช้ Age และ Gender_Dummy เป็นตัวแปรทำนายในแบบจำลองการถดถอย

ตัวอย่างที่ 2: สร้างตัวแปรจำลองที่มีหลายค่า

สมมติว่าเรามีชุดข้อมูลต่อไปนี้และต้องการใช้ สถานภาพสมรส และ อายุ เพื่อทำนาย รายได้ :

หากต้องการใช้ สถานภาพการสมรส เป็นตัวแปรทำนายในแบบจำลองการถดถอย เราจำเป็นต้องแปลงให้เป็นตัวแปรจำลอง

เนื่องจากปัจจุบันนี้เป็นตัวแปรเด็ดขาดที่สามารถรับค่าที่แตกต่างกันได้สามค่า (“โสด”, “แต่งงานแล้ว” หรือ “หย่าร้าง”) เราจึงต้องสร้างตัวแปรจำลอง k -1 = 3-1 = 2 ตัว

ในการสร้างตัวแปรจำลองนี้ เราสามารถปล่อยให้ “เดี่ยว” เป็นค่าฐานได้เนื่องจากปรากฏบ่อยที่สุด ต่อไปนี้คือวิธีที่เราจะแปลง สถานภาพการสมรส เป็นตัวแปรจำลอง:

จากนั้นเราสามารถใช้ Age , Married and Divorced เป็นตัวแปรทำนายในแบบจำลองการถดถอย

วิธีการตีความเอาต์พุตการถดถอยด้วยตัวแปรจำลอง

สมมติว่าเราปรับโมเดล การถดถอยเชิงเส้นพหุคูณ โดยใช้ชุดข้อมูลจากตัวอย่างก่อนหน้านี้ โดยมีตัวแปรตัวทำนายคือ Age , Married และ Divorced และ Income เป็นตัวแปรการตอบสนอง

นี่คือผลลัพธ์ของการถดถอย:

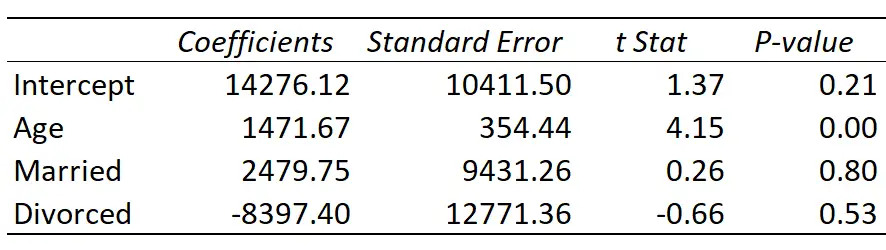
เส้นการถดถอยที่ติดตั้งถูกกำหนดเป็น:

รายได้ = 14,276.21 + 1,471.67*(อายุ) + 2,479.75*(แต่งงานแล้ว) – 8,397.40*(หย่าร้าง)

เราสามารถใช้สมการนี้เพื่อค้นหารายได้โดยประมาณของแต่ละบุคคลโดยพิจารณาจากอายุและสถานภาพการสมรส ตัวอย่างเช่น บุคคลที่อายุ 35 ปีและแต่งงานแล้วจะมีรายได้ประมาณ $68,264 :

รายได้ = 14,276.21 + 1,471.67*(35) + 2,479.75*(1) – 8,397.40*(0) = 68,264 ดอลลาร์

ต่อไปนี้เป็นวิธีการตีความค่าสัมประสิทธิ์การถดถอยในตาราง:

• การสกัดกั้น: การสกัดกั้นแสดงถึงรายได้เฉลี่ยของบุคคลคนเดียวที่มีอายุเป็นศูนย์ แน่นอนว่าคุณไม่สามารถมีปีเป็นศูนย์ได้ ดังนั้นจึงไม่มีเหตุผลที่จะตีความค่าตัดแกนด้วยตัวเองในแบบจำลองการถดถอยเฉพาะนี้
• อายุ: อายุที่เพิ่มขึ้นในแต่ละปีสัมพันธ์กับรายได้ที่เพิ่มขึ้นโดยเฉลี่ย 1,471.67 ดอลลาร์ เนื่องจากค่า p (0.00) น้อยกว่า 0.05 อายุจึงเป็นตัวทำนายรายได้ที่มีนัยสำคัญทางสถิติ
• แต่งงานแล้ว: คนที่แต่งงานแล้วมีรายได้เฉลี่ยมากกว่า 2,479.75 ดอลลาร์สหรัฐฯ มากกว่าคนเดียว เนื่องจากค่า p (0.80) ไม่น้อยกว่า 0.05 ความแตกต่างนี้จึงไม่มีนัยสำคัญทางสถิติ
• หย่าร้าง: บุคคลที่หย่าร้างมีรายได้โดยเฉลี่ย 8,397.40 ดอลลาร์น้อยกว่าบุคคลเดียว เนื่องจากค่า p (0.53) ไม่น้อยกว่า 0.05 ความแตกต่างนี้จึงไม่มีนัยสำคัญทางสถิติ

เนื่องจากตัวแปรจำลองทั้งสองไม่มีนัยสำคัญทางสถิติ เราจึงสามารถลบ สถานภาพการสมรส ซึ่งเป็นตัวทำนายออกจากแบบจำลองได้ เนื่องจากดูเหมือนว่าจะไม่เพิ่มมูลค่าเชิงทำนายให้กับรายได้

แหล่งข้อมูลเพิ่มเติม

ตัวแปรเชิงคุณภาพและเชิงปริมาณ
กับดักตัวแปรจำลอง
วิธีอ่านและตีความตารางการถดถอย
คำอธิบายค่า P และนัยสำคัญทางสถิติ