การถดถอยลอการิทึมใน r (ทีละขั้นตอน)

การถดถอยแบบลอการิทึม เป็นการถดถอยประเภทหนึ่งที่ใช้จำลองสถานการณ์ที่การเติบโตหรือการลดลงเร่งความเร็วอย่างรวดเร็วในช่วงแรก จากนั้นจึงช้าลงเมื่อเวลาผ่านไป

ตัวอย่างเช่น กราฟต่อไปนี้แสดงตัวอย่างการสลายตัวของลอการิทึม:

สำหรับสถานการณ์ประเภทนี้ ความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนองสามารถสร้างแบบจำลองได้ดีโดยใช้การถดถอยแบบลอการิทึม

สมการสำหรับแบบจำลองการถดถอยลอการิทึมมีรูปแบบดังต่อไปนี้:

y = ก + b*ln(x)

ทอง:

• y: ตัวแปรตอบสนอง
• x: ตัวแปรทำนาย
• a, b: สัมประสิทธิ์การถดถอยซึ่งอธิบายความสัมพันธ์ระหว่าง x และ y

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการถดถอยลอการิทึมใน R

ขั้นตอนที่ 1: สร้างข้อมูล

ขั้นแรก เรามาสร้างข้อมูลปลอมสำหรับตัวแปรสองตัวกันก่อน: x และ y :

 x=1:15

y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)

ขั้นตอนที่ 2: แสดงภาพข้อมูล

ต่อไป เรามาสร้างแผนภาพกระจายอย่างรวดเร็วเพื่อให้เห็นภาพความสัมพันธ์ระหว่าง x และ y :

 plot(x, y) 

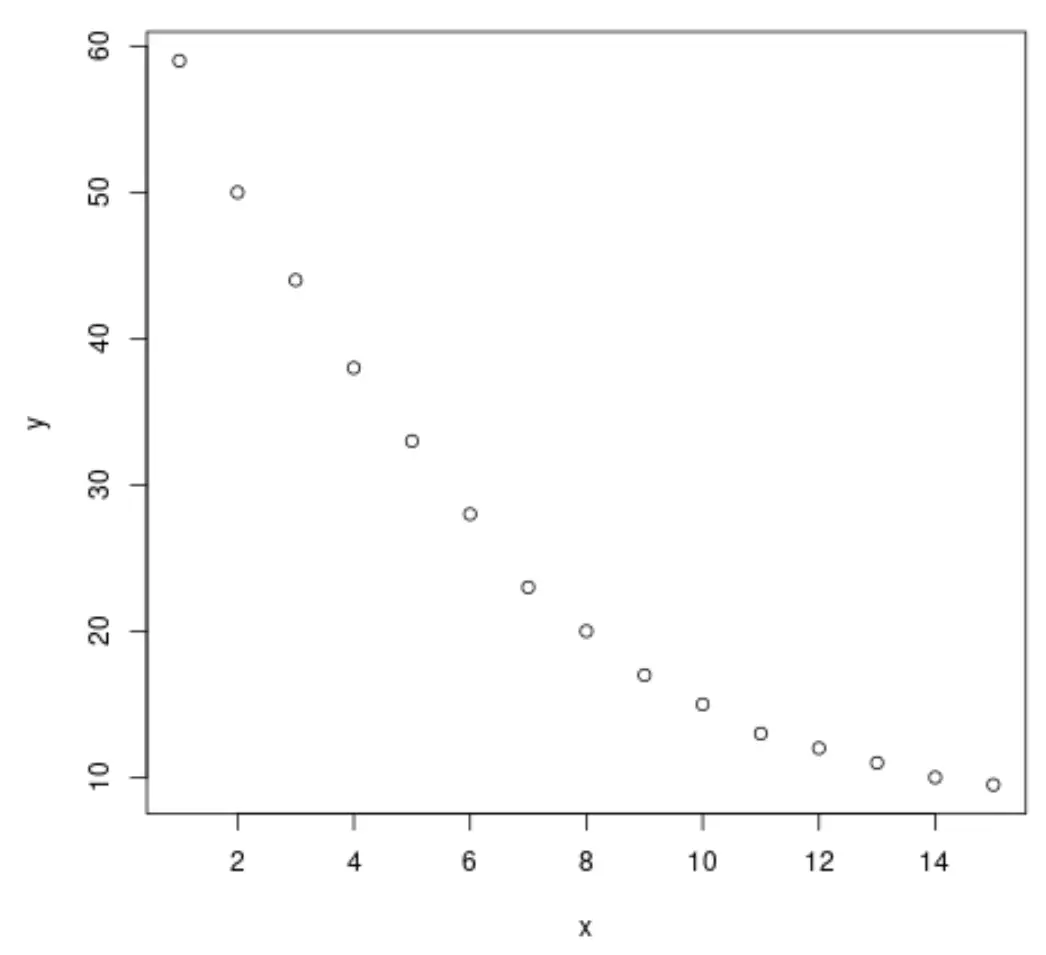
จากกราฟเราจะเห็นได้ว่ามีรูปแบบการสลายตัวแบบลอการิทึมที่ชัดเจนระหว่างตัวแปรทั้งสอง ค่าของตัวแปรตอบสนอง y ลดลงอย่างรวดเร็วในช่วงแรก จากนั้นจึงช้าลงเมื่อเวลาผ่านไป

ดังนั้นจึงเป็นการดีที่จะปรับสมการการถดถอยลอการิทึมเพื่ออธิบายความสัมพันธ์ระหว่างตัวแปรต่างๆ

ขั้นตอนที่ 3: ปรับแบบจำลองการถดถอยลอการิทึม

ต่อไป เราจะใช้ฟังก์ชัน lm() เพื่อให้พอดีกับแบบจำลองการถดถอยลอการิทึม โดยใช้ลอการิทึมธรรมชาติของ x เป็นตัวแปรทำนาย และ y เป็นตัวแปรตอบสนอง

 #fit the model
model <- lm(y ~ log (x))

#view the output of the model
summary(model)

Call:
lm(formula = y ~ log(x))

Residuals:
   Min 1Q Median 3Q Max 
-4.069 -1.313 -0.260 1.127 3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.0686 1.4090 44.76 1.25e-15 ***
log(x) -20.1987 0.7019 -28.78 3.70e-13 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.054 on 13 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 
F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13

ค่า F โดยรวม ของแบบจำลองคือ 828.2 และค่า p ที่สอดคล้องกันนั้นต่ำมาก (3.702e-13) ซึ่งบ่งชี้ว่าแบบจำลองโดยรวมมีประโยชน์

เมื่อใช้ค่าสัมประสิทธิ์จากตารางผลลัพธ์ เราจะเห็นว่าสมการการถดถอยลอการิทึมที่ติดตั้งไว้คือ:

y = 63.0686 – 20.1987 * ln(x)

เราสามารถใช้สมการนี้เพื่อทำนายตัวแปรตอบสนอง y ตามค่าของตัวแปรทำนาย x ตัวอย่างเช่น ถ้า x = 12 เราจะคาดการณ์ว่า y จะเป็น 12.87 :

y = 63.0686 – 20.1987 * ln(12) = 12.87

โบนัส: คุณสามารถใช้เครื่องคำนวณการถดถอยลอการิทึมออนไลน์นี้เพื่อคำนวณสมการการถดถอยลอการิทึมสำหรับตัวแปรทำนายและตัวแปรตอบสนองที่กำหนดโดยอัตโนมัติ

ขั้นตอนที่ 4: แสดงภาพแบบจำลองการถดถอยลอการิทึม

สุดท้ายนี้ เราสามารถสร้างกราฟสั้นๆ เพื่อให้เห็นภาพว่าแบบจำลองการถดถอยแบบลอการิทึมเหมาะสมกับข้อมูลอย่างไร:

 #plot x vs. y
plot(x, y)

#define x-values to use for regression line
x=seq(from= 1 , to= 15 , length. out = 1000 )

#use the model to predict the y-values based on the x-values
y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )),
          interval=" confidence ")

#add the fitted regression line to the plot (lwd specifies the width of the line)
matlines(x,y, lwd= 2 )

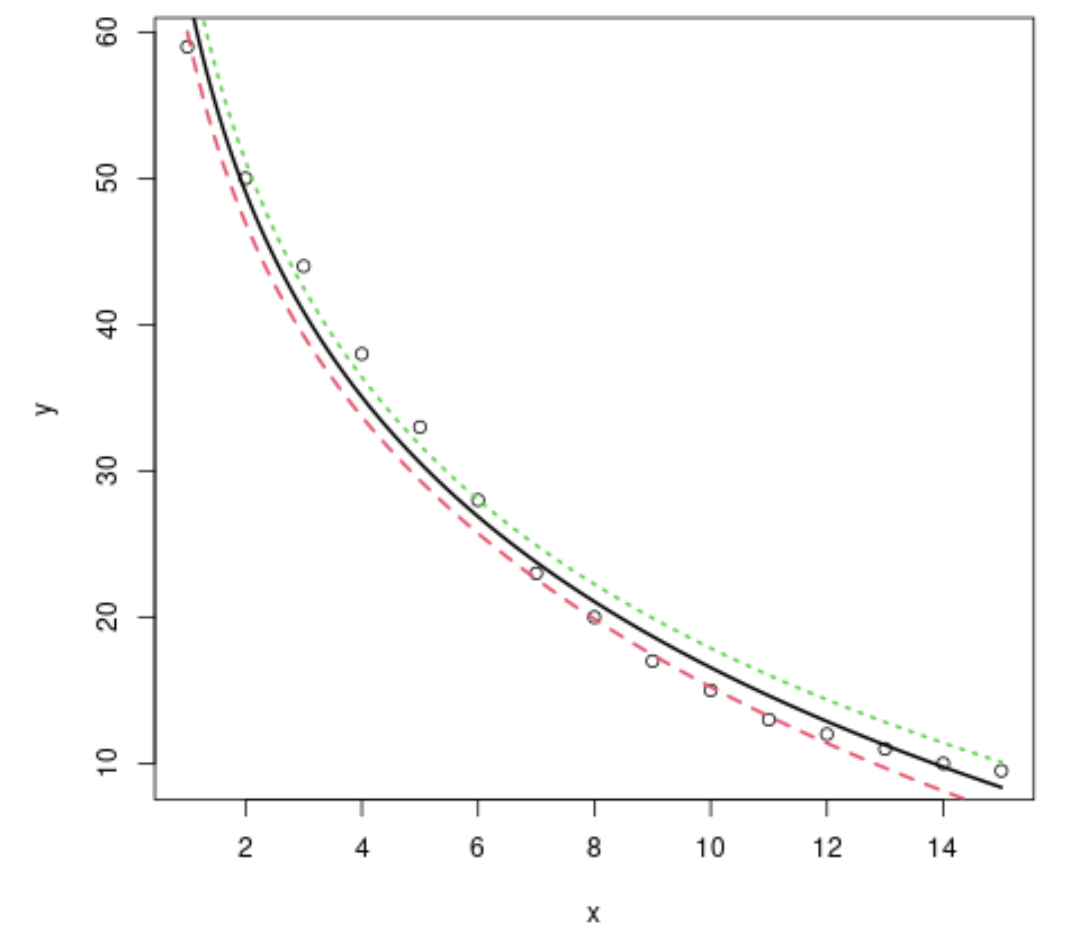
เราจะเห็นว่าแบบจำลองการถดถอยแบบลอการิทึมทำงานได้ดีในการปรับชุดข้อมูลเฉพาะนี้ให้เหมาะสม

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยกำลังสองใน R
วิธีดำเนินการถดถอยเอ็กซ์โปเนนเชียลใน R
วิธีดำเนินการถดถอยพหุนามใน R