ประเภทค่าเฉลี่ย (สถิติ)

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 6, 2023 สถิติ 0 ความคิดเห็น

ที่นี่เราจะอธิบายว่าค่าเฉลี่ยทุกประเภทในสถิติมีอะไรบ้าง และวิธีการคำนวณ คุณจะพบสูตรและตัวอย่างถุงน่องแต่ละประเภท

แต่ก่อนที่จะดูว่าค่าเฉลี่ยเป็นประเภทใด เราต้องรู้อย่างมีเหตุผลว่าค่าเฉลี่ยในสถิติเป็นอย่างไร ดังนั้น เราขอแนะนำให้คุณอ่านลิงก์ต่อไปนี้ก่อนดำเนินการต่อ

➤ ดู: ค่าเฉลี่ย (สถิติ) คืออะไร?

ค่าเฉลี่ยประเภทใดในสถิติ?

ในทางสถิติ ประเภทของค่าเฉลี่ยได้แก่:

ค่าเฉลี่ยเลขคณิต
ถัวเฉลี่ยถ่วงน้ำหนัก
หมายถึงเรขาคณิต
รากหมายถึงสี่เหลี่ยม
ความหมายฮาร์มอนิก
ค่าเฉลี่ยทั่วไป
ค่า f เฉลี่ยทั่วไป
ตัดหมายถึง
ค่าเฉลี่ยระหว่างควอไทล์
ค่าเฉลี่ยของฟังก์ชัน

ต่อไปเราจะอธิบายวิธีคำนวณค่าเฉลี่ยทุกประเภททางสถิติ ค่าเฉลี่ยห้าประเภทที่ใช้บ่อยที่สุด ได้แก่ ค่าเฉลี่ยเลขคณิต ค่าเฉลี่ยถ่วงน้ำหนัก ค่าเฉลี่ยเรขาคณิต ค่าเฉลี่ยกำลังสอง และค่าเฉลี่ยฮาร์มอนิก เราจะมาดูรายละเอียดเพิ่มเติมเกี่ยวกับสื่อหลักทั้ง 5 ประเภทนี้กัน

ค่าเฉลี่ยเลขคณิต

ค่าเฉลี่ยเลขคณิต คำนวณโดยการบวกค่าทั้งหมดแล้วหารด้วยจำนวนจุดข้อมูลทั้งหมด

สูตรสำหรับค่าเฉลี่ยเลขคณิตจึงเป็นดังนี้:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

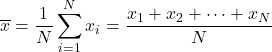
ค่าเฉลี่ยเลขคณิตเรียกอีกอย่างว่า ค่าเฉลี่ยเลขคณิต

ค่าเฉลี่ยเลขคณิตอาจเป็นค่าเฉลี่ยประเภทที่ใช้มากที่สุดในสถิติ

หากต้องการดูตัวอย่างวิธีการรับค่าเฉลี่ยประเภทนี้ เราจะคำนวณค่าเฉลี่ยเลขคณิตของข้อมูลต่อไปนี้:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

ในการคำนวณค่าเฉลี่ยเลขคณิต เพียงบวกข้อมูลทางสถิติทั้งหมดแล้วหารด้วยจำนวนข้อมูลทั้งหมดซึ่งก็คือ 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

ถัวเฉลี่ยถ่วงน้ำหนัก

ใน การคำนวณค่าเฉลี่ยถ่วงน้ำหนัก คุณต้องคูณข้อมูลทางสถิติแต่ละรายการด้วยน้ำหนัก (หรือน้ำหนัก) ก่อน จากนั้นจึงบวกผลคูณทั้งหมด และสุดท้ายหารผลรวมถ่วงน้ำหนักด้วยผลรวมของน้ำหนักทั้งหมด

สูตรถัวเฉลี่ยถ่วงน้ำหนักจึงเป็นดังนี้:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

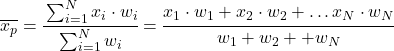
โดยที่ x _i คือค่าทางสถิติ และ _มี น้ำหนักที่สอดคล้องกัน

ค่าเฉลี่ยถ่วงน้ำหนักนั้นเข้าใจยากกว่า ดังนั้นเราขอแนะนำให้ดูตัวอย่างต่อไปนี้ ซึ่งจะอธิบายวิธีการคำนวณทีละขั้นตอน:

➤ ดู ตัวอย่างค่าเฉลี่ยถ่วงน้ำหนัก

หมายถึงเรขาคณิต

ค่าเฉลี่ยเรขาคณิต ของชุดข้อมูลทางสถิติเท่ากับรากที่ n ของผลิตภัณฑ์ของค่าทั้งหมด

ค่าเฉลี่ยประเภทนี้ใช้ในด้านการเงินธุรกิจเพื่อคำนวณอัตราผลตอบแทน เปอร์เซ็นต์ค่าเฉลี่ย และดอกเบี้ยทบต้น

สูตรการจัดเก็บประเภทนี้ค่อนข้างซับซ้อน อันที่จริง ไม่สามารถคำนวณค่าเฉลี่ยเรขาคณิตของชุดทางสถิติทั้งหมดได้ แต่บางครั้งไม่สามารถระบุค่าเฉลี่ยประเภทนี้ได้ นี่คือเหตุผลที่เราขอแนะนำให้คุณศึกษาข้อยกเว้นทั้งหมดที่อธิบายไว้ในลิงก์ต่อไปนี้:

➤ ดู สูตรค่าเฉลี่ยเรขาคณิต

รากหมายถึงสี่เหลี่ยม

ค่าเฉลี่ยรากกำลังสอง เท่ากับรากที่สองของค่าเฉลี่ยเลขคณิตของกำลังสองของข้อมูล

สูตรกำลังสองเฉลี่ยจึงเป็นดังนี้:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

ค่าเฉลี่ยประเภทนี้เรียกอีกอย่างว่า Root Mean Square , Root Mean Square หรือ RMS

เราขอชี้ให้เห็นว่าค่าเฉลี่ยลูกบาศก์ก็มีอยู่เช่นกัน แต่จะใช้ในกรณีพิเศษมาก

การหาค่าเฉลี่ยกำลังสองมีทั้งข้อดีและข้อเสีย เช่น จะมีประโยชน์อย่างยิ่งเมื่อตัวแปรทางสถิติรับค่าบวกและค่าลบ เพราะโดยการยกกำลังสองข้อมูลแต่ละชิ้น ค่าทั้งหมดจะกลายเป็นค่าบวก คุณสามารถดูคุณสมบัติเพิ่มเติมของสื่อประเภทนี้ได้โดยคลิกลิงก์ต่อไปนี้:

➤ ดู: ข้อดีและข้อเสียของกำลังสองเฉลี่ยรูท

ความหมายฮาร์มอนิก

ค่าเฉลี่ยฮาร์มอนิก คำนวณโดยการหารจำนวนข้อมูลทางสถิติทั้งหมดด้วยผลรวมของส่วนกลับของแต่ละค่า

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

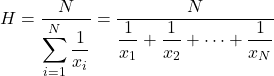
ค่าเฉลี่ยฮาร์มอนิกใช้ในการคำนวณความเร็วเฉลี่ย เวลา หรือทำการคำนวณทางอิเล็กทรอนิกส์ คุณลักษณะนี้ทำให้ค่าเฉลี่ยฮาร์มอนิกแตกต่างจากค่าเฉลี่ยประเภทอื่นๆ ซึ่งมักใช้ในการคำนวณค่าเฉลี่ยราคาหรือเปอร์เซ็นต์

คุณสามารถดูตัวอย่างการคำนวณค่าเฉลี่ยประเภทนี้ได้ในหน้าต่อไปนี้:

➤ ดู: ตัวอย่างความหมายฮาร์มอนิก

ถุงน่องชนิดอื่นๆ

ในส่วนนี้เราจะมาดูสูตรถุงน่องชนิดอื่นๆ กัน เราจะไม่ลงรายละเอียดเกี่ยวกับถุงน่องแต่ละประเภทเนื่องจากไม่ค่อยมีการใช้กันอย่างแพร่หลาย แต่ก็ดีที่จะรู้ว่าถุงน่องชนิดอื่นยังมีอยู่

ค่าเฉลี่ยทั่วไป เป็นส่วนผสมของประเภทค่าเฉลี่ยที่เห็นด้านบน และคำนวณโดยใช้สูตรต่อไปนี้:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

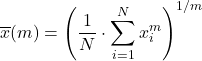
ให้ f เป็นฟังก์ชัน injective และ monotonic จากนั้นค่า f-mean ทั่วไป ที่กำหนดเป็น:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

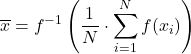
ค่าเฉลี่ยแบบตัดนั้น เกี่ยวข้องกับการคำนวณค่าเฉลี่ยเลขคณิตหลังจากลบเปอร์เซ็นต์ของการสังเกตที่ปลายด้านบนและล่างของกลุ่มตัวอย่าง ควรปฏิเสธเปอร์เซ็นต์เดียวกันที่ปลายทั้งสองข้าง

ในการคำนวณ ค่าเฉลี่ยระหว่างควอไทล์ หรือที่เรียกว่าค่าเฉลี่ยระหว่างควอไทล์ ข้อมูลจากควอร์ไทล์ที่หนึ่งและสี่จะถูกละทิ้งไปเสียก่อน จากนั้นจึงคำนวณค่าเฉลี่ยเลขคณิตของควอไทล์ที่สองและสามของกลุ่มตัวอย่างเท่านั้น สูตรสำหรับค่าเฉลี่ยประเภทนี้จึงเป็นดังนี้:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

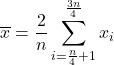
สุดท้ายนี้ คุณยังสามารถหา ค่าเฉลี่ยของฟังก์ชัน ได้ด้วย ค่าเฉลี่ยของฟังก์ชันต่อเนื่องในช่วงเวลาปิด [a,b] คำนวณโดยใช้สูตรต่อไปนี้:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

ตัวอย่างและค่าเฉลี่ยประชากร

สุดท้ายนี้เราจะมาดูกันว่าค่าเฉลี่ยตัวอย่างกับค่าเฉลี่ยประชากรแตกต่างกันอย่างไร ค่าเฉลี่ย 2 ประเภทที่มักสับสนกันคือ

ค่าเฉลี่ยตัวอย่าง คือค่าเฉลี่ยที่คำนวณจากค่าของกลุ่มตัวอย่างทางสถิติ กล่าวคือ คำนวณจากส่วนหนึ่งของค่าทั้งหมดของตัวแปร

ค่าเฉลี่ยประชากร คือค่าเฉลี่ยที่คำนวณจากประชากรทางสถิติ ซึ่งก็คือค่าทั้งหมดของตัวแปร ดังนั้นค่าเฉลี่ยประชากรจึงสอดคล้องกับค่าคาดหวังทางคณิตศาสตร์ของตัวแปร

ค่าเฉลี่ยตัวอย่างถือได้ว่าเป็นค่าเฉลี่ยเท่ากับค่าเฉลี่ยประชากรหากทราบข้อมูลจำนวนมากเพียงพอ แต่มูลค่าของค่าเฉลี่ยประชากรนั้นหาได้ยากมากเนื่องจากในความเป็นจริงแล้วค่าของการแจกแจงทั้งหมดนั้นไม่ค่อยมีใครรู้จัก

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม