เศษเหลือของ pearson คืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)
ส่วนที่เหลือของ Pearson ใช้ใน การทดสอบไคสแควร์ เพื่อวิเคราะห์ความแตกต่างระหว่างจำนวนเซลล์ที่สังเกตได้และจำนวนเซลล์ที่คาดหวังในตารางฉุกเฉิน
สูตรคำนวณ ปริมาณคงเหลือของเพียร์สัน คือ:
r ij = (O ij – E ij ) / √ E ij
ทอง:
- r ij : ส่วนที่เหลือของ Pearson สำหรับเซลล์ของคอลัมน์ที่ i และแถว ที่ j
- O ij : ค่าที่สังเกตได้สำหรับเซลล์ของคอลัมน์ที่ i และแถว ที่ j
- E ij : ค่าที่คาดหวังสำหรับเซลล์ของคอลัมน์ ที่ i และแถว ที่ j
การวัดที่คล้ายกันคือ ค่าคงเหลือของ Pearson ที่ได้มาตรฐาน (ปรับแล้ว) ซึ่งคำนวณได้ดังนี้:
r ij = (O ij – E ij ) / √ E ij (1-n i+ )(1-n +j )
ทอง:
- r ij : ส่วนที่เหลือของ Pearson สำหรับเซลล์ของคอลัมน์ที่ i และแถว ที่ j
- O ij : ค่าที่สังเกตได้สำหรับเซลล์ของคอลัมน์ที่ i และแถว ที่ j
- E ij : ค่าที่คาดหวังสำหรับเซลล์ของคอลัมน์ ที่ i และแถว ที่ j
- p i+ : ผลรวมแถวหารด้วยผลรวมทั้งหมด
- p + j : ผลรวมของคอลัมน์หารด้วยผลรวมทั้งหมด
โดยปกติค่าตกค้างของ Pearson ที่เป็นมาตรฐานจะแจกแจงด้วยค่าเฉลี่ย 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1 ค่าตกค้างของ Pearson ที่ได้มาตรฐานใดๆ ที่มีค่าสัมบูรณ์สูงกว่าเกณฑ์ที่กำหนด (เช่น 2 หรือ 3) บ่งชี้ว่าไม่มีความเหมาะสม
ตัวอย่างต่อไปนี้แสดงวิธีคำนวณปริมาณคงเหลือของ Pearson ในทางปฏิบัติ
ตัวอย่าง: การคำนวณปริมาณคงเหลือของเพียร์สัน
สมมติว่านักวิจัยต้องการใช้การทดสอบไคสแควร์เพื่อตัดสินว่าเพศสัมพันธ์กับการเลือกพรรคการเมืองหรือไม่
พวกเขาตัดสินใจสุ่มตัวอย่างผู้มีสิทธิเลือกตั้ง 500 คน และถามพวกเขาเกี่ยวกับความชอบของพรรคการเมือง
ตารางฉุกเฉินต่อไปนี้จะแสดงผลการสำรวจ:
| รีพับลิกัน | ประชาธิปัตย์ | เป็นอิสระ | ทั้งหมด | |
| ชาย | 120 | 90 | 40 | 250 |
| หญิง | 110 | 95 | 45 | 250 |
| ทั้งหมด | 230 | 185 | 85 | 500 |
ก่อนที่จะคำนวณปริมาณคงเหลือของ Pearson เราต้องคำนวณจำนวนที่คาดหวังสำหรับแต่ละเซลล์ในตารางฉุกเฉินก่อน เมื่อต้องการทำเช่นนี้ เราสามารถใช้สูตรต่อไปนี้:
ค่าที่คาดหวัง = (ผลรวมของแถว * ผลรวมของคอลัมน์) / ผลรวมของตาราง
ตัวอย่างเช่น ค่าที่คาดหวังสำหรับผู้ชายพรรครีพับลิกันคือ: (230*250) / 500 = 115
เราสามารถทำซ้ำสูตรนี้เพื่อให้ได้ค่าที่คาดหวังสำหรับแต่ละเซลล์ของตาราง:
| รีพับลิกัน | ประชาธิปัตย์ | เป็นอิสระ | ทั้งหมด | |
| ชาย | 115 | 92.5 | 42.5 | 250 |
| หญิง | 115 | 92.5 | 42.5 | 250 |
| ทั้งหมด | 230 | 185 | 85 | 500 |
จากนั้นเราจะคำนวณค่า คงเหลือของ Pearson สำหรับแต่ละเซลล์ในตารางได้
ตัวอย่างเช่น จำนวนที่เหลือของเพียร์สันสำหรับห้องขังที่มีชายพรรครีพับลิกันจะถูกคำนวณดังนี้:
- r ij = (O ij – E ij ) / √ E ij
- รี จ = (120 – 115) / √ 115
- รี จ = 0.466
เราสามารถทำซ้ำสูตรนี้เพื่อให้ได้ค่าคงเหลือของ Pearson สำหรับแต่ละเซลล์ในตาราง:
| รีพับลิกัน | ประชาธิปัตย์ | เป็นอิสระ | |
| ชาย | 0.446 | -0.259 | -0.383 |
| หญิง | -0.446 | 0.259 | 0.383 |
จากนั้นเราจะคำนวณ ค่าคงเหลือของ Pearson ที่เป็นมาตรฐาน สำหรับแต่ละเซลล์ในตารางได้
ตัวอย่างเช่น ค่าคงเหลือของเพียร์สันที่เป็นมาตรฐานสำหรับห้องขังที่มีชายจากพรรครีพับลิกันจะถูกคำนวณดังนี้:
- r ij = (O ij – E ij ) / √ E ij (1-p i+ )(1-p +j )
- ริ จ = (120 – 115) / √ 115(1-250/500)(1-230/500)
- รี จ = 0.897
เราสามารถทำซ้ำสูตรนี้เพื่อให้ได้ค่าคงเหลือของ Pearson ที่ได้มาตรฐานสำหรับแต่ละเซลล์ในตาราง:
| รีพับลิกัน | ประชาธิปัตย์ | เป็นอิสระ | |
| ชาย | 0.897 | -0.463 | -0.595 |
| หญิง | -0.897 | 0.463 | 0.595 |
เราจะเห็นได้ว่าไม่มีสารตกค้างของเพียร์สันที่เป็นมาตรฐานที่มีค่าสัมบูรณ์มากกว่า 3 ซึ่งบ่งชี้ว่าไม่มีเซลล์ใดมีส่วนทำให้ขาดความพอดีอย่างมีนัยสำคัญ
หากเราใช้ เครื่องคิดเลขออนไลน์นี้ เพื่อทดสอบความเป็นอิสระของไคสแควร์ เราจะพบว่าค่า p ของการทดสอบคือ 0.649198
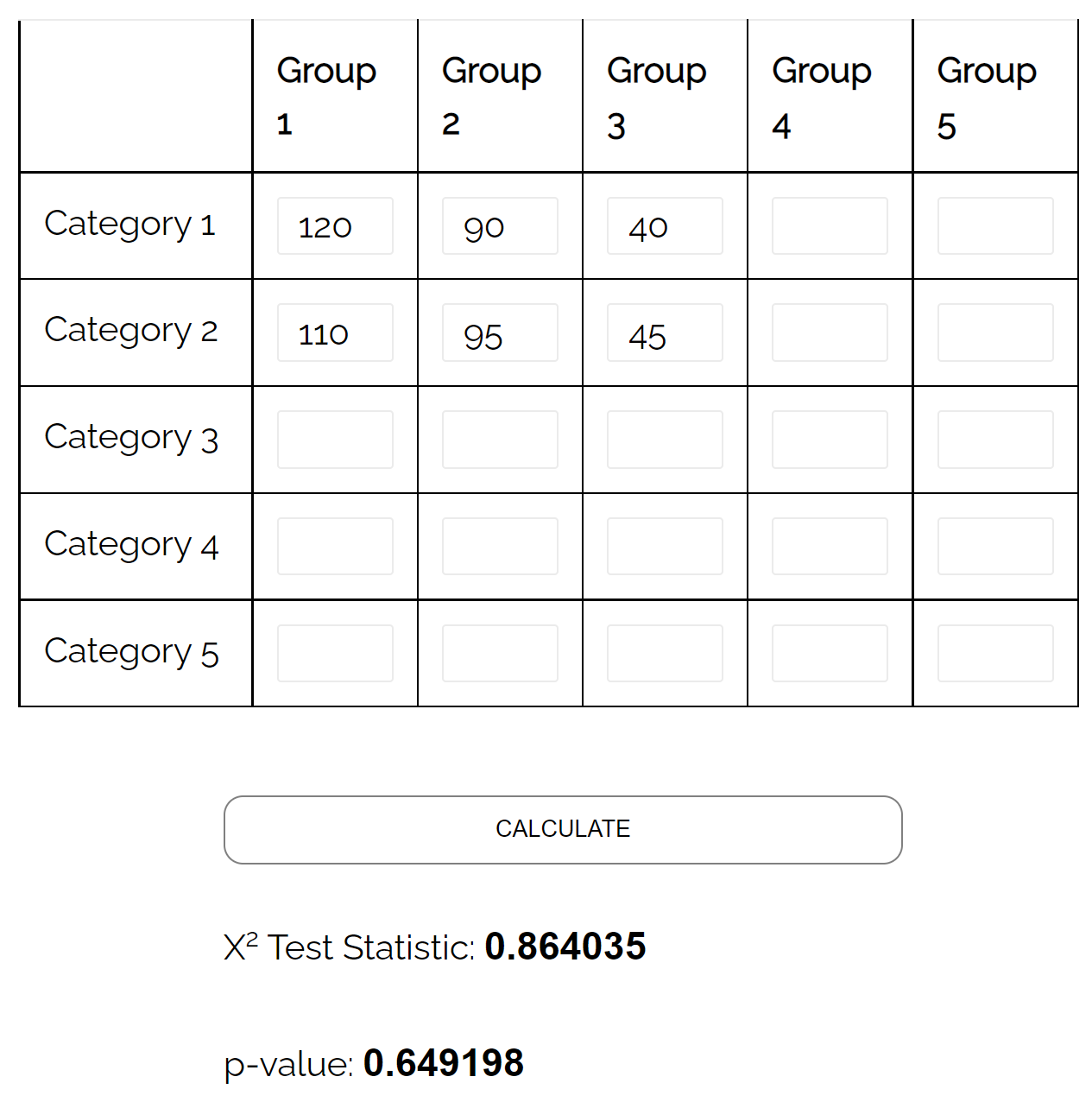
เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่มีหลักฐานเพียงพอที่จะกล่าวว่ามีความสัมพันธ์ระหว่างเพศกับความชอบของพรรคการเมือง
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีการทดสอบความเป็นอิสระของไคสแควร์โดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:
ความรู้เบื้องต้นเกี่ยวกับการทดสอบความเป็นอิสระของไคสแควร์
วิธีการทดสอบความเป็นอิสระของ Chi-Square ใน Excel
วิธีการทดสอบความเป็นอิสระของไคสแควร์ใน R
การทดสอบไคสแควร์ของเครื่องคิดเลขอิสระ