เมื่อใดที่คุณควรใช้ box plot? (3 สถานการณ์)
พล็อตกล่อง คือประเภทของพล็อตที่แสดงข้อมูลสรุปห้าหลักของชุดข้อมูล ซึ่งประกอบด้วย:
- ค่าต่ำสุด
- ควอร์ไทล์ที่หนึ่ง (เปอร์เซ็นไทล์ที่ 25)
- ค่ามัธยฐาน
- ควอไทล์ที่สาม (เปอร์เซ็นไทล์ที่ 75)
- ค่าสูงสุด
เราใช้สามขั้นตอนง่ายๆ เพื่อสร้างพล็อตกล่องสำหรับชุดข้อมูลใดๆ:
- 1. วาดกล่องจากควอไทล์ที่หนึ่งถึงควอไทล์ที่สาม
- 2. ลากเส้นแนวตั้งที่จุดกึ่งกลาง
- 3. วาด “หนวด” ของควอไทล์ให้เป็นค่าต่ำสุดและสูงสุด

โดยทั่วไปเราจะสร้าง boxplots ในหนึ่งในสามสถานการณ์:
สถานการณ์ที่ 1: แสดงภาพการกระจายของค่าในชุดข้อมูล
โครงแบบกล่องช่วยให้เราเห็นภาพการกระจายของค่าในชุดข้อมูลได้อย่างรวดเร็ว และดูว่าค่าสรุปตัวเลขทั้งห้าอยู่ที่ตำแหน่งใด
สถานการณ์ที่ 2: เพื่อเปรียบเทียบการแจกแจงสองรายการขึ้นไป
บ็อกซ์พล็อตแบบเคียงข้างกันช่วยให้เราเห็นภาพความแตกต่างระหว่างการแจกแจงสองค่าขึ้นไปและเปรียบเทียบค่ามัธยฐานและการกระจายของค่าระหว่างการแจกแจง
สถานการณ์ที่ 3: เพื่อระบุค่าผิดปกติ
ในแปลงกล่อง ค่าผิดปกติมักจะแสดงด้วยวงกลมเล็กๆ ที่ขยายออกไปเกินแต่ละหนวด การสังเกตถูกกำหนดให้เป็นค่าผิดปกติหากตรงตามเกณฑ์ข้อใดข้อหนึ่งต่อไปนี้:
- การสังเกตน้อยกว่า Q1 – 1.5*(ช่วงระหว่างควอไทล์)
- การสังเกตมีค่ามากกว่า Q3 + 1.5*(ช่วงระหว่างควอไทล์)
ด้วยการสร้างบ็อกซ์พล็อต เราจะสามารถดูได้อย่างรวดเร็วว่าการแจกแจงมีค่าผิดปกติหรือไม่
ตัวอย่างต่อไปนี้แสดงวิธีที่เราจะใช้การลงจุดแบบกล่องในแต่ละสถานการณ์
สถานการณ์ที่ 1: แสดงภาพการกระจายของค่าในชุดข้อมูล
สมมติว่าโค้ชบาสเกตบอลต้องการแสดงภาพการกระจายคะแนนที่ผู้เล่นในทีมของเขาทำได้ ดังนั้นจึงสร้างโครงเรื่องต่อไปนี้:
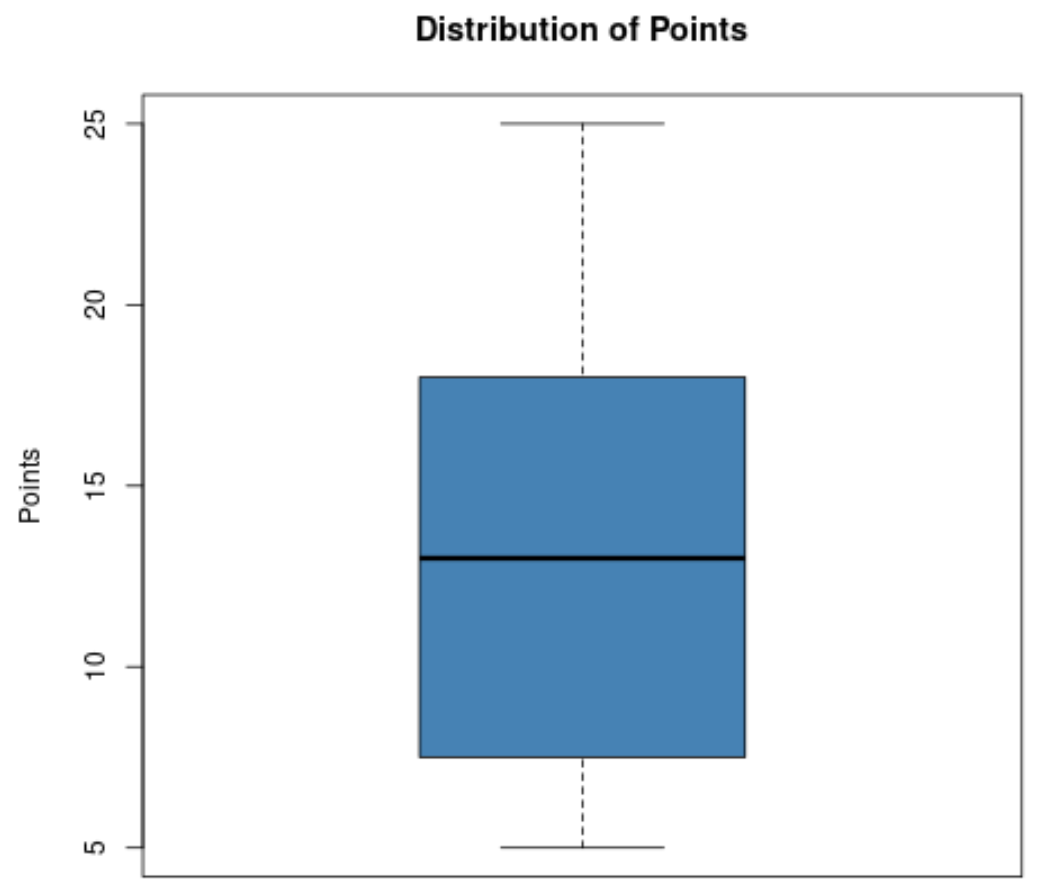
จากพล็อตของกล่องนี้ เขาสามารถเห็นค่าต่อไปนี้ได้อย่างรวดเร็ว:
- ขั้นต่ำ: 5
- T1 (ควอไทล์แรก): ประมาณ 8
- มัธยฐาน: ประมาณ 13
- T3 (ควอไทล์ที่สาม): ประมาณ 18
- สูงสุด: 25
สิ่งนี้ช่วยให้โค้ชเห็นได้อย่างรวดเร็วว่าคะแนนที่ผู้เล่นทำคะแนนได้มีตั้งแต่ 5 ถึง 25 คะแนน โดยคะแนนมัธยฐานที่ทำได้คือประมาณ 13 คะแนน และ 50% ของผู้เล่นของเขาทำคะแนนระหว่างประมาณ 8 ถึง 18 คะแนนต่อเกม
สถานการณ์ที่ 2: เปรียบเทียบการแจกแจงสองรายการขึ้นไป
สมมติว่านักวิเคราะห์กีฬาต้องการเปรียบเทียบการกระจายคะแนนของผู้เล่นบาสเก็ตบอลในทีมที่แตกต่างกัน 3 ทีม และสร้างแผนผังช่องต่อไปนี้
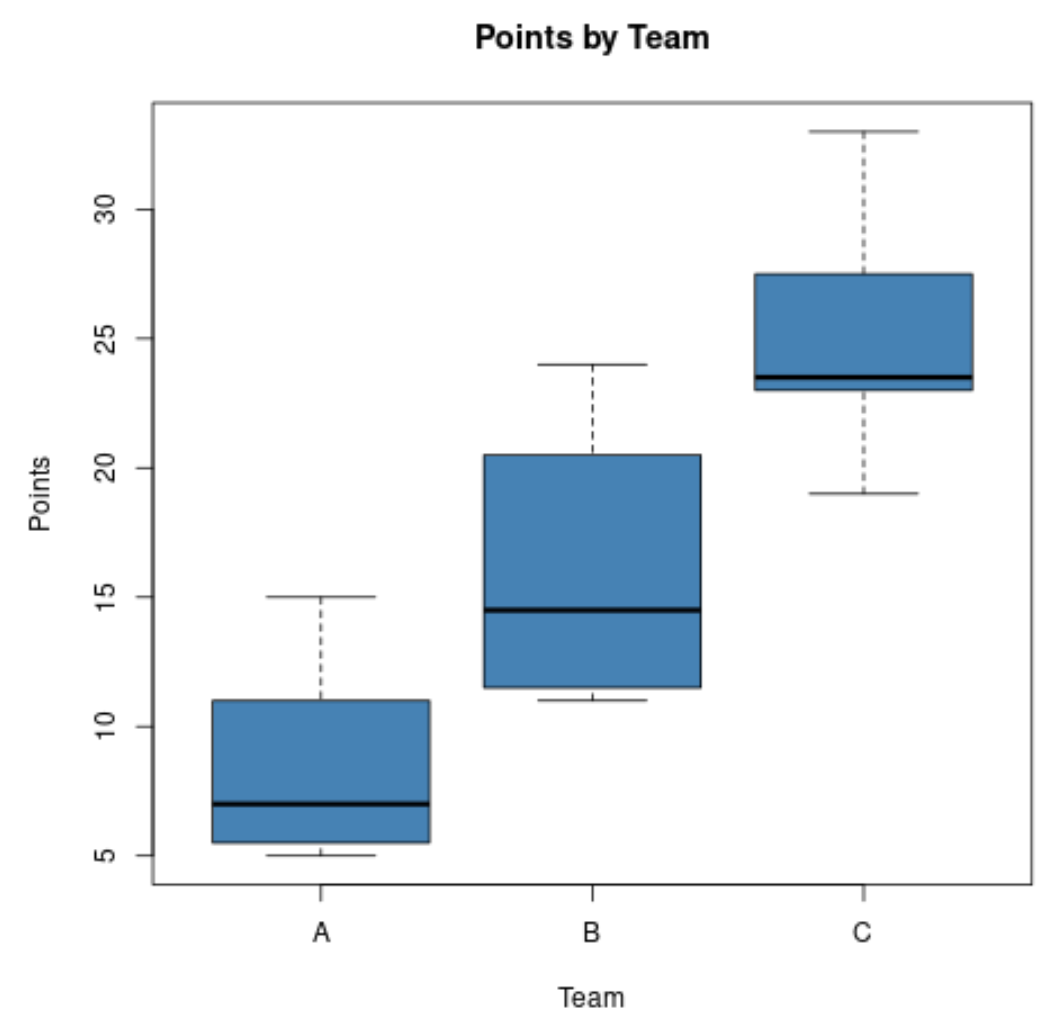
เมื่อใช้กราฟเหล่านี้ เขาสามารถเห็นได้อย่างรวดเร็วว่าทีม C มีคะแนนกึ่งกลางสูงสุด และทีม A มีคะแนนกึ่งกลางต่ำสุด
เขายังสามารถเห็นได้อย่างรวดเร็วว่าทีม B มีการกระจายคะแนนมากที่สุดเนื่องจากแผนภูมิกล่องของทีม B มีกล่องที่ยาวที่สุด
สถานการณ์ที่ 3: ระบุค่าผิดปกติ
สมมติว่าโค้ชบาสเกตบอลต้องการทราบว่าผู้เล่นคนใดคนหนึ่งของเขามีค่าผิดปกติในแง่ของคะแนนที่ทำได้ เขาตัดสินใจสร้างกล่องพล็อตต่อไปนี้เพื่อให้เห็นภาพการกระจายคะแนนที่ผู้เล่นของเขาทำได้:
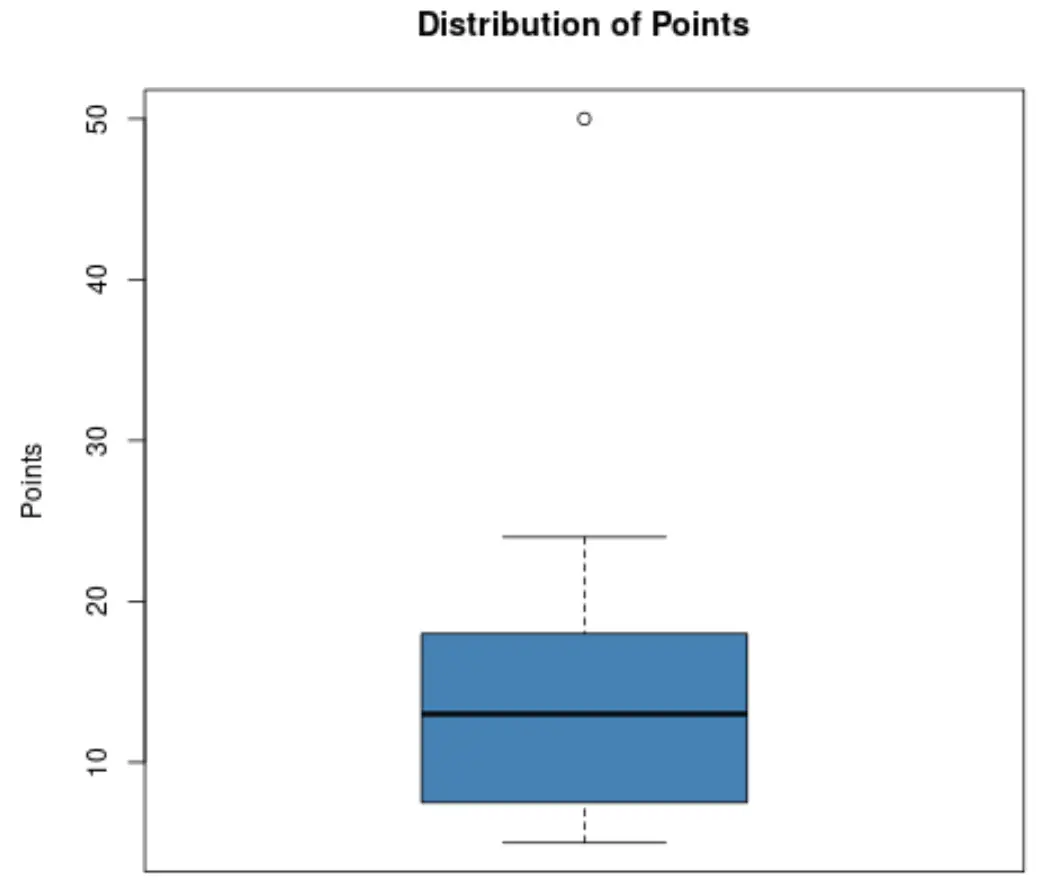
เมื่อใช้โครงเรื่องนี้ โค้ชจะเห็นว่าจุดเล็กๆ ที่ด้านบนของโครงเรื่องบ่งบอกถึงค่าผิดปกติ
โดยเฉพาะอย่างยิ่ง ผู้เล่นคนหนึ่งทำคะแนนได้ประมาณ 50 คะแนน ซึ่งถือว่าผิดปกติเมื่อเทียบกับคะแนนอื่นๆ ทั้งหมดที่ทำคะแนนได้
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้นำเสนอคำอธิบายโดยละเอียดเกี่ยวกับวิธีการใช้ boxplots ในทางปฏิบัติ:
วิธีค้นหาช่วงระหว่างควอไทล์ (IQR) ของ Box Plot
วิธีการระบุความไม่สมมาตรในแปลงกล่อง
วิธีเปรียบเทียบแปลงกล่อง
บทช่วยสอนต่อไปนี้จะอธิบายวิธีสร้างกล่องแปลงในซอฟต์แวร์ทางสถิติต่างๆ:
วิธีสร้าง Box Plot ใน Google ชีต
วิธีสร้างกล่องแปลงใน SPSS
วิธีการสร้างแปลงกล่องแบบเคียงข้างกันใน Excel
วิธีการสร้างพล็อตกล่องแบบเคียงข้างกันใน R