การกระจายไวบูล

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบ Weibull คืออะไร และใช้เพื่ออะไร นอกจากนี้ คุณยังจะได้เห็นการแสดงกราฟิกของการแจกแจงแบบ Weibull และคุณสมบัติของการแจกแจงความน่าจะเป็นประเภทนี้

การกระจายแบบ Weibull คืออะไร?

การแจกแจงแบบ Weibull เป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่องที่กำหนดโดยพารามิเตอร์ลักษณะเฉพาะสองตัว ได้แก่ พารามิเตอร์รูปร่าง α และพารามิเตอร์มาตราส่วน γ

ในทางสถิติ การแจกแจงแบบ Weibull ใช้สำหรับการวิเคราะห์ความอยู่รอดเป็นหลัก ในทำนองเดียวกัน การกระจาย Weibull มีการใช้งานมากมายในสาขาต่างๆ เราจะลงรายละเอียดเกี่ยวกับการใช้การแจกแจงแบบ Weibull ด้านล่าง

$X\sim\text{Weibull}(\alpha,\lambda)$

ตามที่ผู้เขียนระบุ การแจกแจงแบบ Weibull สามารถกำหนดพารามิเตอร์ได้ด้วยพารามิเตอร์สามตัว จากนั้นจะมีการเพิ่มพารามิเตอร์ตัวที่สามที่เรียกว่าค่าเกณฑ์ ซึ่งบ่งชี้ถึงจุดหักล้างที่กราฟการกระจายเริ่มต้น

การแจกแจงแบบ Weibull ตั้งชื่อตาม Waloddi Weibull ชาวสวีเดน ซึ่งอธิบายรายละเอียดไว้ในปี 1951 อย่างไรก็ตาม การแจกแจงแบบ Weibull ถูกค้นพบโดย Maurice Fréchet ในปี 1927 และนำไปใช้ครั้งแรกโดย Rosin และ Rammler ในปี 1933

การวางแผนการแจกแจงแบบไวบูล

เมื่อเราได้เห็นคำจำกัดความของการแจกแจงแบบ Weibull แล้ว เราจะดูว่าการแสดงกราฟิกของมันแตกต่างกันอย่างไรขึ้นอยู่กับค่าของพารามิเตอร์

ด้านล่างนี้ คุณสามารถดูตัวอย่างต่างๆ ได้ว่ากราฟฟังก์ชันความหนาแน่นของการแจกแจงแบบไวบูลแปรผันอย่างไร โดยขึ้นอยู่กับค่าของพารามิเตอร์รูปร่างและพารามิเตอร์มาตราส่วน

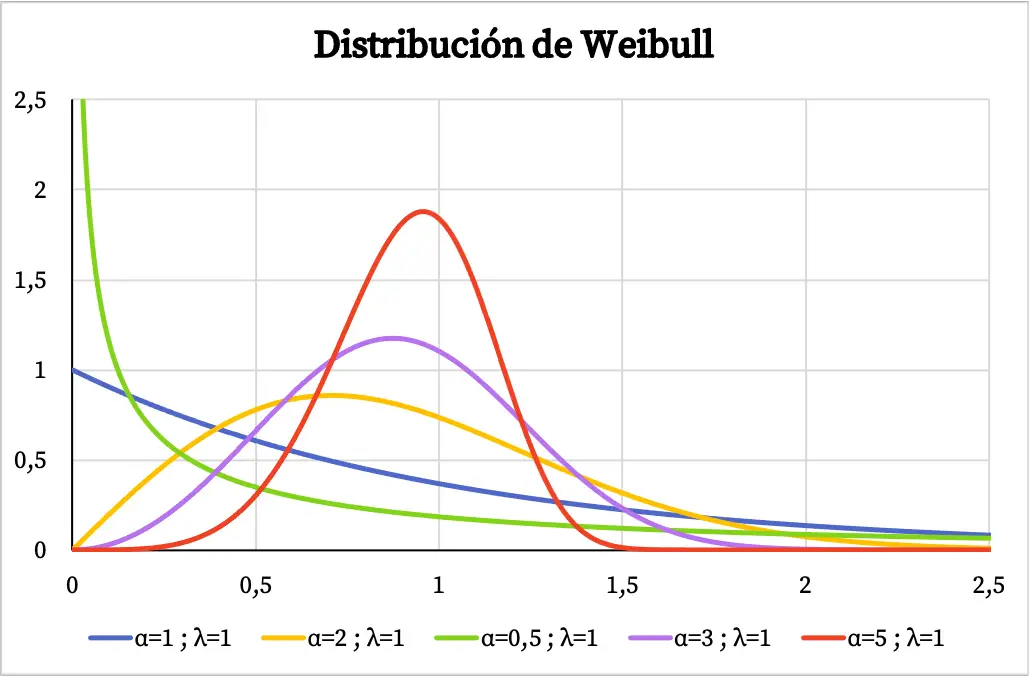
เมื่อใช้การแจกแจงแบบไวบูลเพื่อจำลองอัตราความล้มเหลวของระบบตามฟังก์ชันของเวลา ค่าของพารามิเตอร์รูปร่าง α จะหมายถึงสิ่งต่อไปนี้:

α<1: อัตราความล้มเหลวลดลงเมื่อเวลาผ่านไป
α=1: อัตราความล้มเหลวคงที่เมื่อเวลาผ่านไป
α>1: อัตราความล้มเหลวเพิ่มขึ้นเมื่อเวลาผ่านไป

ในทางกลับกัน ในกราฟต่อไปนี้ คุณจะเห็นฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบ Weibull ที่พล็อตตามค่าคุณลักษณะของมัน

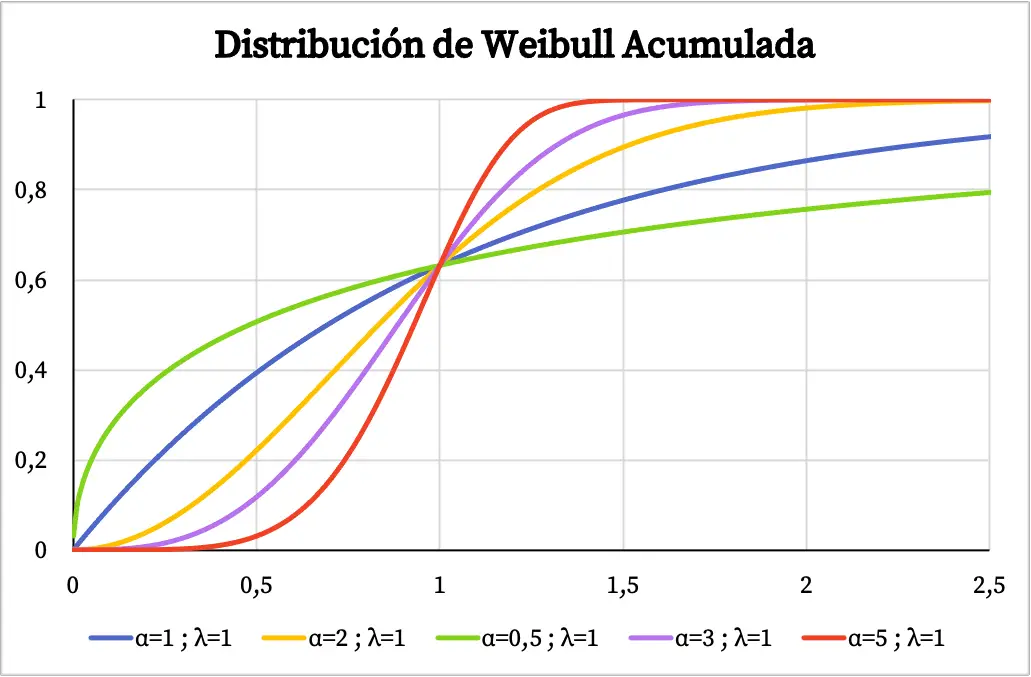
ลักษณะเฉพาะของการแจกแจงแบบไวบูล

การกระจายแบบ Weibull มีลักษณะดังต่อไปนี้:

การแจกแจงแบบ Weibull มีพารามิเตอร์ลักษณะเฉพาะสองตัวที่กำหนดกราฟ: พารามิเตอร์รูปร่าง α และพารามิเตอร์มาตราส่วน แล พารามิเตอร์ทั้งสองเป็นจำนวนจริงบวก

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p> </p> <ul> <li> การแจกแจงแบบ Weibull ยอมรับเฉพาะค่า Abscissa ที่เป็นบวกเท่านั้น</li> </ul> <p class=$ $x\in (0,+\infty)$

ค่าเฉลี่ยของการแจกแจงแบบ Weibull คำนวณโดยใช้สูตรต่อไปนี้:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

ในทางกลับกัน สูตรการหาความแปรปรวนของการแจกแจงแบบไวบูลคือ:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

โหมดของตัวแปรสุ่มที่ตามหลังการแจกแจงแบบไวบูลด้วย α>1 สามารถกำหนดได้โดยนิพจน์ต่อไปนี้:

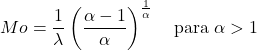
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”50″ width=”257″ style=”vertical-align: -17px;”></p> </p> <ul> <li> สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจงแบบไวบูลคือ:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

ในทำนองเดียวกัน สูตรสำหรับฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบไวบูลคือ:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

ค่าสัมประสิทธิ์ความไม่สมมาตรของการแจกแจงแบบ Weibull คำนวณโดยใช้สูตรต่อไปนี้:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

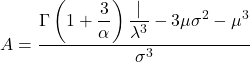
ในที่สุด สูตรที่ทำให้สามารถกำหนดค่าสัมประสิทธิ์ความโด่งของการแจกแจงแบบไวบูลได้มีดังต่อไปนี้:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

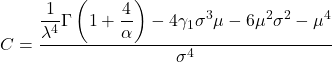
ทอง

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

การประยุกต์ใช้การกระจายแบบ Weibull

การกระจาย Weibull มีการใช้งานมากมาย ได้แก่ :

ในสถิติประยุกต์ การแจกแจงแบบไวบูลใช้ในการวิเคราะห์การอยู่รอด
ในทางวิศวกรรม การแจกแจงแบบ Weibull ใช้เพื่อจำลองฟังก์ชันที่เกี่ยวข้องกับเวลาในการผลิต
ในระบบเรดาร์เพื่อจำลองการกระจายตัวของสัญญาณที่ได้รับ
ในภาคการประกันภัย เพื่อสร้างแบบจำลองขอบเขตของการเรียกร้อง
ตัวอย่างเช่นในอุตุนิยมวิทยา เพื่อจำลองความถี่ของความเร็วลมที่แตกต่างกัน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม