แม่ vs. rmse: คุณควรใช้เมตริกใด
แบบจำลองการถดถอยใช้ในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายหนึ่งตัวขึ้นไปกับ ตัวแปรตอบสนอง
เมื่อใดก็ตามที่เราพอดีกับโมเดลการถดถอย เราต้องการเข้าใจว่าโมเดลสามารถใช้ค่าของตัวแปรทำนายเพื่อทำนายค่าของตัวแปรตอบสนองได้ดีเพียงใด
ตัวชี้วัดสองตัวที่เรามักใช้เพื่อหาปริมาณว่าแบบจำลองเหมาะสมกับชุดข้อมูลได้ดีเพียงใด ได้แก่ ค่าคลาดเคลื่อนค่าเฉลี่ยสัมบูรณ์ (MAE) และค่าความผิดพลาดรากกำลังสองเฉลี่ย (RMSE) ซึ่งคำนวณได้ดังนี้:
MAE : ตัวชี้วัดที่บอกเราถึงความแตกต่างสัมบูรณ์โดยเฉลี่ยระหว่างค่าที่คาดการณ์กับค่าจริงในชุดข้อมูล ยิ่ง MAE ต่ำ โมเดลก็ยิ่งเหมาะกับชุดข้อมูลมากขึ้นเท่านั้น
แม่ = 1/n * Σ|y i – ŷ i |
ทอง:
- Σ เป็นสัญลักษณ์ที่หมายถึง “ผลรวม”
- y คือค่าที่สังเกตได้สำหรับการสังเกต ครั้งที่ 3
- ŷ i คือค่าที่ทำนายไว้สำหรับการสังเกต ครั้งที่ i
- n คือขนาดตัวอย่าง
RMSE : ตัวชี้วัดที่บอกเราถึงรากที่สองของรากที่สองหมายถึงผลต่างกำลังสองระหว่างค่าที่คาดการณ์กับค่าจริงในชุดข้อมูล ยิ่ง RMSE ต่ำ โมเดลก็จะเหมาะกับชุดข้อมูลมากขึ้นเท่านั้น
มีการคำนวณดังนี้:
RMSE = √ Σ(y ฉัน – ŷ i ) 2 / n
ทอง:
- Σ เป็นสัญลักษณ์ที่หมายถึง “ผลรวม”
- ŷ i คือค่าที่ทำนายไว้สำหรับการสังเกต ครั้งที่ i
- y คือค่าที่สังเกตได้สำหรับการสังเกต ครั้งที่ 3
- n คือขนาดตัวอย่าง
ตัวอย่าง: การคำนวณ RMSE และ MAE
สมมติว่าเราใช้แบบจำลองการถดถอยเพื่อทำนายว่าผู้เล่น 10 คนจะทำคะแนนในเกมบาสเก็ตบอลได้กี่คะแนน
ตารางต่อไปนี้แสดงคะแนนที่แบบจำลองทำนายไว้เปรียบเทียบกับคะแนนจริงที่ผู้เล่นทำได้:

การใช้เครื่องคิดเลข MAE เราสามารถคำนวณได้ว่า MAE คือ 3.2
สิ่งนี้บอกเราว่าความแตกต่างสัมบูรณ์โดยเฉลี่ยระหว่างค่าที่คาดการณ์โดยแบบจำลองกับค่าจริงคือ 3.2
เมื่อใช้ เครื่องคิดเลข RMSE เราสามารถคำนวณได้ว่า RMSE เท่ากับ 4
นี่บอกเราว่ารากที่สองของรากหมายถึงผลต่างกำลังสองระหว่างคะแนนที่คาดการณ์ไว้กับคะแนนที่ได้จริงคือ 4
โปรดทราบว่าแต่ละเมตริกทำให้เราทราบถึงความแตกต่างโดยทั่วไประหว่างค่าที่คาดการณ์โดยแบบจำลองและค่าจริงในชุดข้อมูล แต่การตีความของแต่ละเมตริกจะแตกต่างกันเล็กน้อย
RMSE กับ MAE: คุณควรใช้เมตริกใด
หากคุณต้องการกำหนดน้ำหนักมากขึ้นให้กับการสังเกตที่อยู่ห่างจากค่าเฉลี่ย (เช่น ถ้าค่าเบี่ยงเบน 20 มากกว่าสองเท่าแย่กว่าค่าเบี่ยงเบน 10) ควรใช้ RMSE เพื่อวัดข้อผิดพลาด เนื่องจาก RMSE เป็น มีความไวต่อการสังเกตมากกว่าค่าเฉลี่ย
อย่างไรก็ตาม หาก “ออฟเซ็ต” ที่ 20 นั้นแย่เป็นสองเท่าของการ “ออฟเซ็ต” ที่ 10 ก็ควรใช้ MAE จะดีกว่า
เพื่ออธิบายสิ่งนี้ สมมติว่าเรามีผู้เล่นที่มีค่าผิดปกติที่ชัดเจนในแง่ของจำนวนคะแนนที่ทำได้:
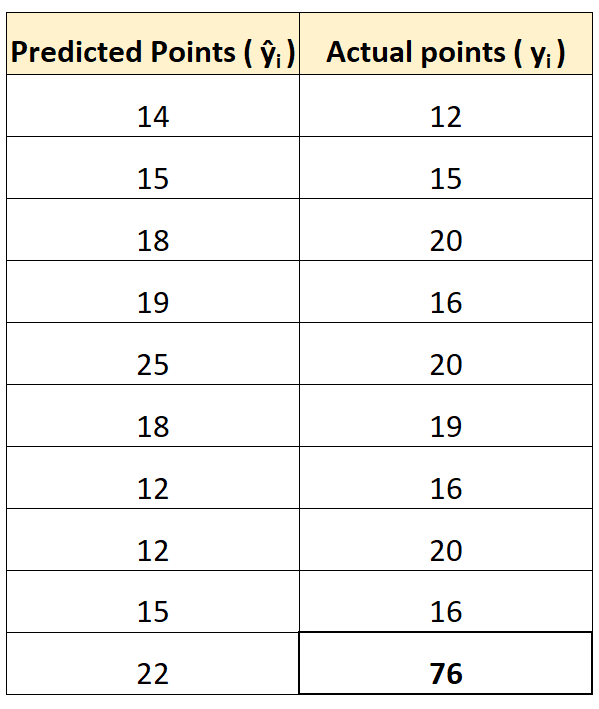
การใช้เครื่องคิดเลขออนไลน์ที่กล่าวถึงข้างต้น ทำให้เราสามารถคำนวณ MAE และ RMSE ได้ดังนี้:
- แม่ : 8
- RMSE : 16.4356
โปรดทราบว่า RMSE เพิ่มขึ้นมากกว่า MAE มาก
เนื่องจาก RMSE ใช้ผลต่างกำลังสองในสูตร และผลต่างกำลังสองระหว่างค่าที่สังเกตได้คือ 76 และค่าที่คาดการณ์ไว้คือ 22 นั้นค่อนข้างมาก ส่งผลให้ค่า RMSE เพิ่มขึ้นอย่างมีนัยสำคัญ
ในทางปฏิบัติ โดยทั่วไปแล้ว เราจะใส่โมเดลการถดถอยหลายตัวเข้ากับชุดข้อมูล และคำนวณหน่วยเมตริกเหล่านี้เพียงตัวเดียวสำหรับแต่ละโมเดล
ตัวอย่างเช่น เราสามารถใส่โมเดลการถดถอยที่แตกต่างกันสามแบบและคำนวณ RMSE สำหรับแต่ละโมเดลได้ จากนั้นเราจะเลือกแบบจำลองที่มีค่า RMSE ต่ำสุดเป็นแบบจำลองที่ “ดีที่สุด” เนื่องจากเป็นแบบจำลองที่ทำให้การคาดการณ์ใกล้เคียงกับค่าจริงในชุดข้อมูลมากที่สุด
ไม่ว่าในกรณีใด เพียงตรวจสอบให้แน่ใจว่าคุณคำนวณเมตริกเดียวกันสำหรับแต่ละรุ่น ตัวอย่างเช่น อย่าคำนวณ MAE สำหรับรุ่นหนึ่งและ RMSE สำหรับรุ่นอื่น แล้วเปรียบเทียบการวัดทั้งสองนี้
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีคำนวณ MAE โดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:
วิธีการคำนวณค่าเฉลี่ยข้อผิดพลาดสัมบูรณ์ใน Excel
วิธีการคำนวณค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์ใน R
วิธีการคำนวณค่าเฉลี่ยข้อผิดพลาดสัมบูรณ์ใน Python
บทช่วยสอนต่อไปนี้อธิบายวิธีคำนวณ RMSE โดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:
วิธีการคำนวณข้อผิดพลาด Mean Square ใน Excel
วิธีการคำนวณค่าคลาดเคลื่อนกำลังสองเฉลี่ยใน R
วิธีการคำนวณ Mean Squared Error ใน Python