ทำความเข้าใจการทดสอบทีในการถดถอยเชิงเส้น
การถดถอยเชิงเส้น ใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนอง
เมื่อใดก็ตามที่เราทำการถดถอยเชิงเส้น เราต้องการทราบว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างตัวแปรทำนายและตัวแปรตอบสนองหรือไม่
เราทดสอบนัยสำคัญโดยทำการทดสอบทีสำหรับความชันการถดถอย เราใช้สมมติฐานว่างและทางเลือกต่อไปนี้สำหรับการทดสอบทีนี้:
- H 0 : β 1 = 0 (ความชันเท่ากับศูนย์)
- HA : β 1 ≠ 0 (ความชันไม่เท่ากับศูนย์)
จากนั้นเราคำนวณสถิติการทดสอบดังนี้:
เสื้อ = b / SE ข
ทอง:
- b : การประมาณค่าสัมประสิทธิ์
- SE b : ความคลาดเคลื่อนมาตรฐานของการประมาณค่าสัมประสิทธิ์
หากค่า p ที่สอดคล้องกับ t ต่ำกว่าเกณฑ์ที่กำหนด (เช่น α = 0.05) เราจะปฏิเสธสมมติฐานว่างและสรุปว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างตัวแปรทำนายและตัวแปรตอบสนอง
ตัวอย่างต่อไปนี้แสดงวิธีการทดสอบทีสำหรับแบบจำลองการถดถอยเชิงเส้นในทางปฏิบัติ
ตัวอย่าง: การรันการทดสอบทีสำหรับการถดถอยเชิงเส้น
สมมติว่าศาสตราจารย์ต้องการวิเคราะห์ความสัมพันธ์ระหว่างชั่วโมงเรียนกับคะแนนสอบของนักเรียน 40 คน
โดยจะทำการถดถอยเชิงเส้นอย่างง่ายโดยใช้ชั่วโมงที่ศึกษาเป็นตัวแปรทำนายและคะแนนการสอบที่ได้รับเป็นตัวแปรตอบสนอง
ตารางต่อไปนี้แสดงผลลัพธ์ของแบบจำลองการถดถอย:
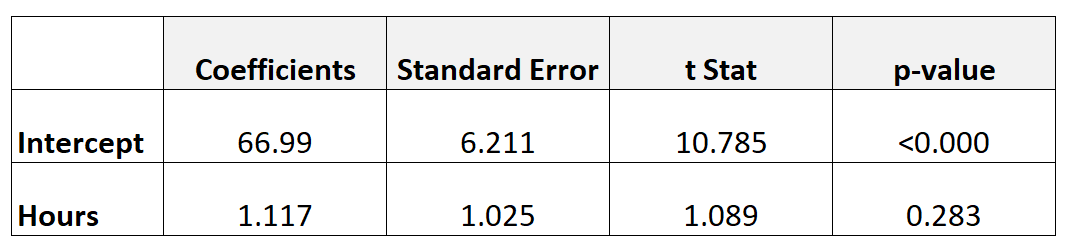
เพื่อตรวจสอบว่าชั่วโมงเรียนมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับคะแนนสอบปลายภาคหรือไม่ เราสามารถทำการทดสอบทีได้
เราใช้สมมติฐานว่างและทางเลือกต่อไปนี้สำหรับการทดสอบทีนี้:
- H 0 : β 1 = 0 (ความชันของชั่วโมงที่ศึกษาเท่ากับศูนย์)
- H A : β 1 ≠ 0 (ความชันของชั่วโมงที่ศึกษาไม่เท่ากับศูนย์)
จากนั้นเราคำนวณสถิติการทดสอบดังนี้:
- เสื้อ = b / SE ข
- เสื้อ = 1.117 / 1.025
- เสื้อ = 1.089
ค่า p ที่สอดคล้องกับ t = 1.089 โดยมี df = n-2 = 40 – 2 = 38 คือ 0.283
โปรดทราบว่าเรายังสามารถใช้ เครื่องคำนวณคะแนน T ถึงค่า P เพื่อคำนวณค่า p นี้ได้ด้วย:

เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
ซึ่งหมายความว่าชั่วโมงเรียน ไม่มี ความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างผลการสอบปลายภาค
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับการถดถอยเชิงเส้น:
รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นอย่างง่าย
รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นพหุคูณ
วิธีการตีความค่าสัมประสิทธิ์การถดถอย
วิธีตีความการทดสอบ F สำหรับนัยสำคัญโดยรวมในการถดถอย