การกระจายพาเรโต

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบ Pareto คืออะไรในสถิติ และใช้เพื่ออะไร คุณจะสามารถดูกราฟการแจกแจงแบบพาเรโตและคุณสมบัติของการแจกแจงความน่าจะเป็นประเภทนี้ได้

การกระจายพาเรโตคืออะไร?

การแจกแจงแบบพาเรโต เป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่องที่ใช้ในสถิติเพื่อจำลองหลักการของพาเรโต ดังนั้นการแจกแจงแบบพาเรโตจึงเป็นการแจกแจงความน่าจะเป็นที่มีค่าไม่กี่ค่าซึ่งความน่าจะเป็นที่จะเกิดขึ้นจะสูงกว่าค่าที่เหลือมาก

โปรดจำไว้ว่ากฎของพาเรโตหรือที่เรียกว่ากฎ 80-20 เป็นหลักการทางสถิติที่บอกว่าสาเหตุของปรากฏการณ์ส่วนใหญ่เกิดจากประชากรส่วนน้อย

การแจกแจงแบบพาเรโตมีพารามิเตอร์ลักษณะเฉพาะสองตัว: พารามิเตอร์มาตราส่วน x _m และพารามิเตอร์รูปร่าง α

$X\sim \text{Pareto}(\alpha,x_m)$

เดิมที การแจกแจงแบบพาเรโตใช้เพื่ออธิบายการกระจายความมั่งคั่งภายในประชากร เนื่องจากส่วนใหญ่มีสาเหตุมาจากสัดส่วนที่น้อยของประชากร แต่ปัจจุบันการจำหน่าย Pareto มีการใช้งานหลายอย่าง เช่น ในการควบคุมคุณภาพ เศรษฐศาสตร์ วิทยาศาสตร์ ในสาขาสังคม เป็นต้น

การแจกแจงแบบพาเรโตตั้งชื่อตามนักเศรษฐศาสตร์ วิลเฟรโด ปาเรโต ซึ่งเป็นผู้กำหนดการกระจาย อย่างไรก็ตาม เขาเป็นที่รู้จักดีที่สุดจากแผนภูมิ Pareto

➤ ดู: แผนภูมิ Pareto คืออะไร

ตารางการกระจายพาเรโต

ตอนนี้เรารู้คำจำกัดความของการแจกแจงแบบพาเรโตแล้ว เรามาดูตัวอย่างต่างๆ ของการแจกแจงแบบพาเรโตที่แสดงเป็นภาพกัน

ด้านล่างนี้คุณจะเห็นได้ว่ากราฟของฟังก์ชันความหนาแน่นของการแจกแจงแบบพาเรโตนั้นมีลักษณะอย่างไร ขึ้นอยู่กับค่าคุณลักษณะ:

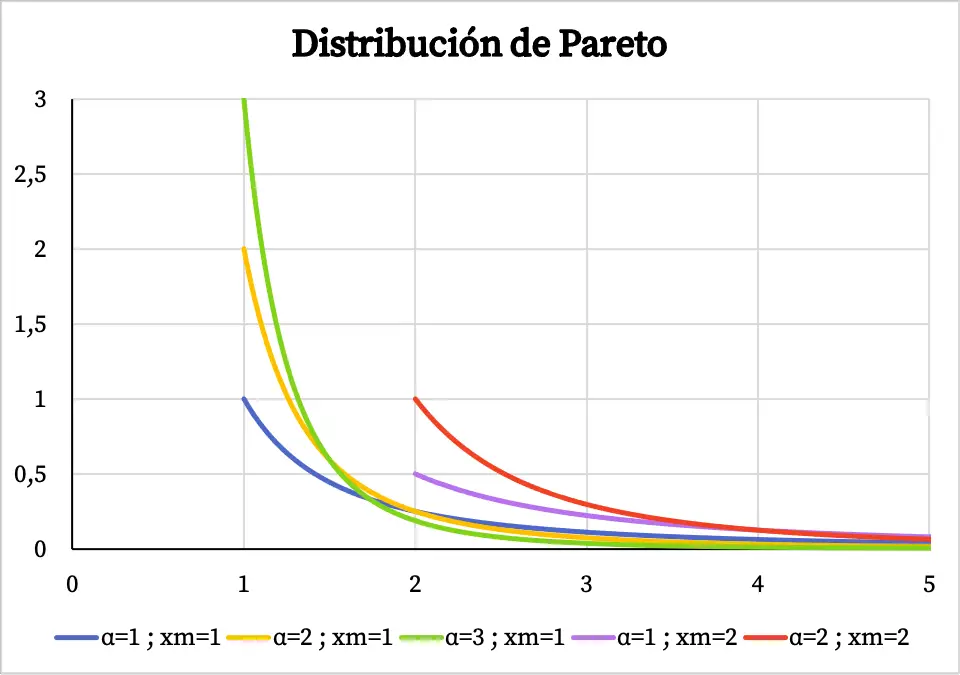
โปรดทราบว่าโดเมนของการแจกแจงแบบพาเรโตเปลี่ยนจากค่า x _m ถึง +∞ ซึ่งเป็นสาเหตุที่ไม่มีฟังก์ชันความหนาแน่นอยู่ก่อนค่า x _m

ในทางกลับกัน กราฟของฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบพาเรโตจะเป็นดังนี้:

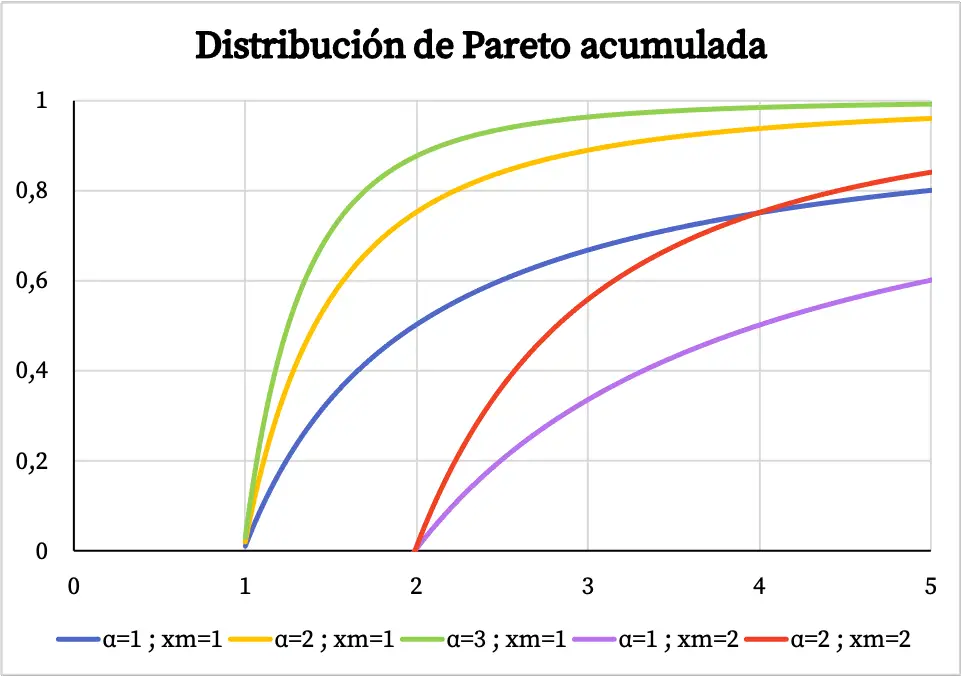
ลักษณะเฉพาะของการแจกแจงแบบพาเรโต

ด้านล่างนี้เป็นคุณลักษณะที่สำคัญที่สุดของการแจกแจงแบบพาเรโตที่เกี่ยวข้องกับทฤษฎีและสถิติความน่าจะเป็น

การแจกแจงแบบพาเรโตมีพารามิเตอร์ลักษณะเฉพาะสองตัวที่กำหนดเส้นโค้ง: พารามิเตอร์มาตราส่วน x _m และพารามิเตอร์รูปร่าง α

$X\sim \text{Pareto}(\alpha,x_m)$

โดเมนของการแจกแจงแบบพาเรโตประกอบด้วยจำนวนจริงทั้งหมดตั้งแต่พารามิเตอร์มาตราส่วนไปจนถึงบวกอนันต์

$x\in [x_m,+\infty)$

ถ้า α มากกว่า 1 ค่าเฉลี่ยของการแจกแจงแบบพาเรโตจะเท่ากับผลคูณของ α คูณ x _m และ α ลบ 1

$E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”> <ul> <li> ความแปรปรวนของการแจกแจงแบบพาเรโตขึ้นอยู่กับพารามิเตอร์ลักษณะเฉพาะสองตัวของการแจกแจง และคำนวณด้วยสูตรต่อไปนี้:</li> </ul> 2″ title=”Rendered by QuickLaTeX.com” height=”44″ width=”323″ style=”vertical-align: -17px;”> <ul> <li> ค่ามัธยฐานของการแจกแจงแบบพาเรโตสามารถกำหนดได้ด้วยนิพจน์ต่อไปนี้:</li> </ul> <p class=$ $\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}$

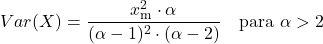
โหมดของการแจกแจงแบบ Pareto เทียบเท่ากับพารามิเตอร์มาตราส่วน x _m ของการแจกแจง

$Mo=x_m$

สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจงแบบพาเรโตคือ:

$\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m$

ในทำนองเดียวกัน สูตรสำหรับฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบพาเรโตคือ:

$\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha$

ค่าสัมประสิทธิ์ความไม่สมมาตรของการแจกแจงแบบพาเรโตขึ้นอยู่กับพารามิเตอร์รูปร่าง α เท่านั้น และการแสดงออกของมันคือ:

$\displaystyle A=\frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\quad\text{para }\alpha>3″ title=”Rendered by QuickLaTeX.com” height=”43″ width=”274″ style=”vertical-align: -14px;”> <ul> <li> ค่าสัมประสิทธิ์ความโด่งของการแจกแจงแบบ Pareto ก็แตกต่างกันไปขึ้นอยู่กับค่าของพารามิเตอร์ α และคำนวณโดยใช้สูตรต่อไปนี้:</li> </ul> 4″ title=”Rendered by QuickLaTeX.com” height=”44″ width=”299″ style=”vertical-align: -17px;”> </div>  <div class=$

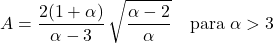
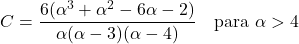
เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การกระจายพาเรโตคืออะไร?

ตารางการกระจายพาเรโต

ลักษณะเฉพาะของการแจกแจงแบบพาเรโต

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น