การแจกแจงแบบทวินาม

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบทวินามในสถิติคืออะไร และใช้เพื่ออะไร ดังนั้นคุณจะพบคำจำกัดความของการแจกแจงแบบทวินาม ตัวอย่างของการแจกแจงแบบทวินาม และคุณสมบัติของการแจกแจงความน่าจะเป็นประเภทนี้ นอกจากนี้ คุณจะสามารถคำนวณความน่าจะเป็นของการแจกแจงทวินามด้วยเครื่องคิดเลขออนไลน์ได้

การแจกแจงแบบทวินามคืออะไร?

การแจกแจงแบบทวินาม เป็นการแจกแจงความน่าจะเป็นที่นับจำนวนความสำเร็จเมื่อทำการทดลองอิสระแบบแบ่งขั้วโดยมีความน่าจะเป็นที่จะสำเร็จคงที่

กล่าวอีกนัยหนึ่ง การแจกแจงแบบทวินามคือการแจกแจงที่อธิบายจำนวนผลลัพธ์ที่สำเร็จของลำดับการทดลองเบอร์นูลลี

โปรดจำไว้ว่าการทดสอบเบอร์นูลลีเป็นการทดลองที่มีผลลัพธ์ที่เป็นไปได้สองแบบ: “ความสำเร็จ” และ “ความล้มเหลว” ดังนั้น หากความน่าจะเป็นของ “ความสำเร็จ” คือ p ความน่าจะเป็นของ “ความล้มเหลว” จะเป็น q=1-p

โดยทั่วไป จำนวนการทดลองทั้งหมดที่ดำเนินการจะถูกกำหนดด้วยพารามิเตอร์ n ในขณะที่ p คือความน่าจะเป็นของความสำเร็จของการทดสอบแต่ละครั้ง ดังนั้นตัวแปรสุ่มที่ตามหลังการแจกแจงแบบทวินามจึงเขียนได้ดังนี้

$X\sim\text{Bin}(n,p)$

โปรดทราบว่าในการแจกแจงแบบทวินาม การทดลองเดียวกันนั้นซ้ำกัน n ครั้ง และการทดลองนั้นเป็นอิสระจากกัน ดังนั้นความน่าจะเป็นที่จะสำเร็จของการทดลองแต่ละครั้งจึงเท่ากัน (p)

การแจกแจงแบบทวินามสามารถเรียกอีกอย่างว่า การแจกแจงแบบทวินาม

ตัวอย่างการแจกแจงแบบทวินาม

เมื่อเราได้เห็นคำจำกัดความของการแจกแจงแบบทวินามแล้ว เราจะเห็นตัวอย่างตัวแปรต่างๆ ที่เป็นไปตามการแจกแจงประเภทนี้เพื่อทำความเข้าใจแนวคิดนี้ให้ดีขึ้น

จำนวนครั้งที่หัวปรากฏเมื่อโยนเหรียญ 25 ครั้ง
จำนวนช็อตที่นักบาสเก็ตบอลยิงเข้าห่วงตาข่าย 60 ครั้งจากตำแหน่งเดียวกัน
จำนวนครั้งที่เราได้เลข 6 โดยการทอยลูกเต๋า 30 ครั้ง
จำนวนผู้สอบผ่านจากนักเรียนที่เข้าสอบทั้งหมด 50 คน
จำนวนหน่วยที่ชำรุดในตัวอย่างสินค้า 100 รายการ

สูตรการกระจายแบบทวินาม

เมื่อพิจารณาจากพารามิเตอร์ x, n, p ฟังก์ชันความน่าจะเป็นของการแจกแจงแบบทวินามถูกกำหนดให้เป็นจำนวนเชิงรวมกันของ n ใน x คูณ p ^x คูณ (1-p) ^nx

ดังนั้น สูตรในการคำนวณความน่าจะเป็นของการแจกแจงแบบทวินาม คือ:

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความน่าจะเป็นของตัวแปรที่ตามหลังการแจกแจงแบบทวินาม

ในทางกลับกัน ความน่าจะเป็นสะสมของการแจกแจงแบบทวินามจะคำนวณโดยการบวกความน่าจะเป็นของจำนวนกรณีปัญหาที่ประสบความสำเร็จและความน่าจะเป็นก่อนหน้านี้ทั้งหมด ดังนั้น สูตรในการคำนวณความน่าจะเป็นสะสมของการแจกแจงแบบทวินามคือ:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

แก้แบบฝึกหัดเรื่องการแจกแจงแบบทวินาม

เราโยนเหรียญ 10 ครั้ง ความน่าจะเป็นที่จะออกหัว 6 ครั้งเป็นเท่าไหร่?

ตัวแปรในปัญหานี้เป็นไปตามการแจกแจงแบบทวินาม เนื่องจากการเปิดตัวทั้งหมดเป็นอิสระจากกันและยังมีความน่าจะเป็นที่จะประสบความสำเร็จเท่ากันอีกด้วย

โดยสรุปแล้ว ความน่าจะเป็นที่จะประสบความสำเร็จคือ 50% เนื่องจากมีเพียงหนึ่งในสองผลลัพธ์ที่เป็นไปได้เท่านั้นที่ถือว่าประสบความสำเร็จ

$p=\cfrac{1}{2}=0,5$

ดังนั้น การแจกแจงสำหรับแบบฝึกหัดนี้เป็นทวินามที่มีการทดลองทั้งหมด 10 ครั้งและความน่าจะเป็น 0.5

$X\sim\text{Bin}(10 ; 0,5)$

ดังนั้น เพื่อหาความน่าจะเป็นที่จะได้หัว 6 หัว เราจำเป็นต้องใช้สูตรการแจกแจงแบบทวินาม

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

ดังนั้น ความน่าจะเป็นที่จะได้หัวหกแต้มอย่างแน่นอนโดยการโยนเหรียญสิบครั้งคือ 20.51%

ลักษณะของการแจกแจงแบบทวินาม

การแจกแจงทวินามมีลักษณะดังต่อไปนี้:

การแจกแจงแบบทวินามถูกกำหนดด้วยพารามิเตอร์สองตัว: n คือจำนวนการทดลองเบอร์นูลลีทั้งหมด และในทางกลับกัน p คือความน่าจะเป็นที่จะสำเร็จของการทดลองเบอร์นูลลีแต่ละครั้ง

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

ค่าเฉลี่ยของการแจกแจงแบบทวินามเท่ากับผลคูณของจำนวนการทดลองทั้งหมดคูณด้วยความน่าจะเป็นที่จะสำเร็จของการทดลองแต่ละครั้ง ดังนั้น ในการคำนวณค่าเฉลี่ยของการแจกแจงแบบทวินาม เราจะต้องคูณ n ด้วย p

$E[X]=n\cdot p$

ความแปรปรวนของการแจกแจงแบบทวินามเท่ากับจำนวนการทดลองทั้งหมดคูณด้วยความน่าจะเป็นที่จะสำเร็จและความน่าจะเป็นที่จะล้มเหลว

$Var(X)=n\cdot p\cdot (1-p)$

สูตรสำหรับฟังก์ชันความน่าจะเป็นของการแจกแจงแบบทวินามมีดังนี้

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

ในทำนองเดียวกัน สูตรสำหรับฟังก์ชันการแจกแจงสะสมของการแจกแจงแบบทวินามคือ:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

ผลรวมของการแจกแจงแบบทวินามอิสระสองตัวที่มีความน่าจะเป็นเท่ากันจะเท่ากับการแจกแจงแบบทวินามที่มีค่าความน่าจะเป็นเท่ากัน p และ n คือผลรวมของจำนวนการทดลองทั้งหมดของการแจกแจงทั้งสองแบบ

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

การแจกแจงแบบเบอร์นูลลีเป็นกรณีพิเศษของการแจกแจงแบบทวินาม โดยที่ n=1 กล่าวคือ มีการทดลองเพียงครั้งเดียวเท่านั้น

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_ถ้า _X 1 , _X ₂ ,…, X _k เป็นตัวแปรสุ่มอิสระเช่นนั้น

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

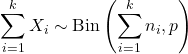
เครื่องคำนวณการกระจายทวินาม

ป้อนค่าของพารามิเตอร์ p, n และ x ของการแจกแจงแบบทวินามลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณความน่าจะเป็น คุณต้องเลือกความน่าจะเป็นที่คุณต้องการคำนวณและป้อนตัวเลขโดยใช้จุดเป็นตัวคั่นทศนิยม เช่น 0.1667

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม