ช่วงความมั่นใจสำหรับสัดส่วน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าช่วงความเชื่อมั่นสำหรับสัดส่วนคืออะไร และใช้เพื่ออะไรในสถิติ ในทำนองเดียวกัน คุณจะได้ค้นพบวิธีการคำนวณช่วงความเชื่อมั่นของสัดส่วน ตลอดจนแบบฝึกหัดที่แก้ไขได้เพื่อให้เข้าใจแนวคิดได้ดีขึ้น

ช่วงความเชื่อมั่นของสัดส่วนคือเท่าไร?

ช่วงความเชื่อมั่นสำหรับสัดส่วน คือช่วงที่ให้ช่วงของค่าที่ยอมรับได้สำหรับสัดส่วนของประชากร นั่นคือ ช่วงความเชื่อมั่นสำหรับสัดส่วนจะระบุค่าสูงสุดและค่าต่ำสุดซึ่งสัดส่วนประชากรอยู่ระหว่างค่าคลาดเคลื่อน

ตัวอย่างเช่น หากช่วงความเชื่อมั่นสำหรับสัดส่วนของประชากรที่มีระดับความเชื่อมั่น 95% คือ (0.73, 0.81) นั่นหมายความว่าสัดส่วนของประชากรอยู่ระหว่าง 73% ถึง 81% ด้วยความน่าจะเป็น 95%

ดังนั้นช่วงความเชื่อมั่นของสัดส่วนจึงถูกใช้เพื่อประมาณมูลค่าของสัดส่วนของประชากรที่ตรงตามคุณลักษณะบางประการ

ดังที่เราจะเห็นในหัวข้อถัดไป ช่วงความเชื่อมั่นสำหรับสัดส่วนนั้นขึ้นอยู่กับสัดส่วนตัวอย่างและจำนวนการสังเกตในกลุ่มตัวอย่าง

สูตรช่วงความเชื่อมั่นสำหรับสัดส่วน

ช่วงความเชื่อมั่นสำหรับสัดส่วนคำนวณโดยการบวกและลบค่าของ Z _α/2 ออกจากสัดส่วนตัวอย่างด้วยรากที่สองของสัดส่วนตัวอย่าง (p) คูณด้วย 1-p และหารด้วยขนาดตัวอย่าง (n) ดังนั้น สูตรในการคำนวณช่วงความเชื่อมั่นของสัดส่วน คือ:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

ทอง:

$p$

คือสัดส่วนตัวอย่าง
$n$

คือขนาดตัวอย่าง
$Z_{\alpha/2}$

คือควอไทล์ของการแจกแจงแบบปกติมาตรฐานที่สอดคล้องกับความน่าจะเป็นของ α/2 สำหรับกลุ่มตัวอย่างขนาดใหญ่และระดับความเชื่อมั่น 95% มักจะใกล้กับ 1.96 และสำหรับระดับความเชื่อมั่น 99% มักจะใกล้กับ 2.576

ตัวอย่างการคำนวณช่วงความเชื่อมั่นสำหรับสัดส่วน

เพื่อให้คุณสามารถดูวิธีการคำนวณช่วงความเชื่อมั่นสำหรับสัดส่วน เราจึงแสดงตัวอย่างที่เป็นรูปธรรมทีละขั้นตอนไว้ด้านล่าง

บริษัทประกันภัยแห่งหนึ่งต้องการวิจัยตลาดและพิจารณาว่าในประเทศหนึ่งๆ มีประกันชีวิตกี่คน โดยสุ่มตัวอย่างจำนวน 700 คนมาวิเคราะห์ และสรุปได้ว่า 40% ของกลุ่มตัวอย่างมีประกันชีวิต ช่วงความเชื่อมั่นที่ระดับความเชื่อมั่น 95% สำหรับสัดส่วนประชากรของประเทศคือเท่าใด

เพื่อกำหนดช่วงความเชื่อมั่นของสัดส่วนประชากร เราจำเป็นต้องใช้สูตรที่เราเห็นข้างต้น:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

ในกรณีนี้ เราต้องการให้ระดับความเชื่อมั่นของช่วงความเชื่อมั่นเป็น 95% ดังนั้นค่าของ Z _α/2 ที่เราต้องใช้คือ 1.96

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

ข้อความเกี่ยวกับปัญหาบอกเราแล้วว่าขนาดของกลุ่มตัวอย่างคือ n=700 และสัดส่วนที่สังเกตได้ในกลุ่มตัวอย่างคือ p=0.40 ดังนั้นเราจึงแทนที่ข้อมูลลงในสูตรช่วงความเชื่อมั่นสำหรับสัดส่วนและคำนวณขีดจำกัดของช่วงดังกล่าว:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

$\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)$

$\displaystyle \left(0,36 \ , \ 0,44\right)$

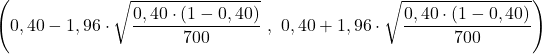
โดยสรุป สัดส่วนของประชากรที่ศึกษาอยู่ระหว่าง 36% ถึง 44% โดยมีระดับความเชื่อมั่น 95%

➤ ดู: ช่วงความเชื่อมั่นสำหรับค่าเฉลี่ย
➤ ดู: ช่วงความเชื่อมั่นสำหรับความแปรปรวน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

ช่วงความเชื่อมั่นของสัดส่วนคือเท่าไร?

สูตรช่วงความเชื่อมั่นสำหรับสัดส่วน

ตัวอย่างการคำนวณช่วงความเชื่อมั่นสำหรับสัดส่วน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น