ความแปรปรวน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่า quasivariance คืออะไรในสถิติ ดังนั้น คุณจะค้นพบวิธีการคำนวณความควอซิวาเรียนซ์ แบบฝึกหัดที่แก้ไขได้ และอะไรคือความแตกต่างระหว่างความควอซิวาเรียนซ์และความแปรปรวน นอกจากนี้ คุณยังสามารถคำนวณความแปรผันของชุดข้อมูลใดๆ ได้ด้วยเครื่องคิดเลขออนไลน์

ความคงตัวคืออะไร?

ในสถิติ quasivariance คือการวัดการกระจายตัวที่บ่งบอกถึงความแปรปรวนของตัวอย่าง แม่นยำยิ่งขึ้น quasivariance เท่ากับผลรวมของกำลังสองของการเบี่ยงเบนหารด้วยจำนวนการสังเกตทั้งหมดลบด้วยหนึ่ง

สัญลักษณ์ของความแปรปรวนคือ

$\sigma_{n-1}^2$

ทั้ง

$s_{n-1}^2$

. บางครั้งถึงแม้จะใช้สัญลักษณ์ก็ตาม

$\widehat{s}^2$

เพื่อแสดงถึงความคงตัว

Quasivariance ใช้เพื่อกำหนดการกระจายตัวของตัวอย่างในขณะที่หลีกเลี่ยงอคติ ซึ่งเป็นสาเหตุว่าทำไมจึงมักเรียกว่าความแปรปรวนที่เป็นกลาง ความแปรปรวนจึงเป็นตัวประมาณที่ดีของความแปรปรวนของประชากร ที่จริงแล้ว เมื่อคำนวณความแปรปรวนตัวอย่าง มักใช้สูตรความแปรปรวนเสมือนแทนสูตรความแปรปรวน ด้านล่างนี้เราจะอธิบายรายละเอียดเกี่ยวกับความแตกต่างระหว่างการวัดทางสถิติทั้งสองนี้

สูตรควอซิวาริแอนซ์

ในการคำนวณความควอซิวาเรียนซ์ เราจำเป็นต้องค้นหาผลรวมของกำลังสองของความแตกต่างระหว่างค่าและค่าเฉลี่ยของชุดข้อมูล แล้วหารด้วยจำนวนข้อมูลทั้งหมดลบด้วยหนึ่ง

ดังนั้น สูตรคำนวณความแปรปรวน มีดังนี้

ทอง:

$\sigma_{n-1}^2$

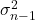
คือความแปรปรวน
$x_i$

คือค่าข้อมูล

$i$

.
$n$

คือจำนวนข้อมูลทั้งหมด
$\overline{X}$

คือค่าเฉลี่ยของชุดข้อมูล

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความแปรผันของชุดข้อมูลใดๆ ได้

คุณอาจสงสัยว่าทำไมมันถึงถูกหารด้วย n-1 ไม่ใช่ด้วย n? มันเกี่ยวกับการกำจัดอคติ วิธีนี้ทำให้เราได้ตัวประมาณที่ไม่เอนเอียง นี่คือสาเหตุที่แน่ชัดว่าทำไมความแปรปรวนของตัวแปรจึงเป็นตัวประมาณที่ดีของความแปรปรวนของประชากร

ตัวอย่างการคำนวณความคงตัว

ตอนนี้เรารู้คำจำกัดความของความควอซิวาเรียนซ์แล้ว เราจะแก้ตัวอย่างง่ายๆ เพื่อให้คุณเห็นว่าควอซิวาเรียนซ์ของชุดข้อมูลคำนวณอย่างไร

จากบริษัทข้ามชาติแห่งหนึ่ง เราทราบถึงผลลัพธ์ทางเศรษฐกิจที่เกิดขึ้นในช่วงห้าปีที่ผ่านมา ส่วนใหญ่ได้รับผลกำไร แต่หนึ่งปีกลับขาดทุนอย่างมาก: 11.5, 2, -9, 7 ล้านยูโร คำนวณความแปรผันของชุดข้อมูลนี้

สิ่งแรกที่เราต้องทำเพื่อให้ได้ค่าความแปรปรวนของชุดข้อมูลคือการคำนวณค่าเฉลี่ยเลขคณิต:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

และเมื่อเรารู้ค่าเฉลี่ยของข้อมูลแล้ว เราก็ใช้สูตรความแปรปรวน:

$\sigma_{n-1}^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

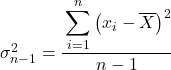
ดังนั้นเราจึงแทนที่ข้อมูลที่ให้ไว้ในคำแนะนำการออกกำลังกายลงในสูตร:

$\sigma_{n-1}^2=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5-1}$

ในที่สุดก็เพียงพอที่จะแก้ไขการดำเนินการเพื่อคำนวณความแปรปรวน:

$\begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}$

โปรดทราบว่าหน่วยของความแปรปรวนเป็นหน่วยเดียวกับหน่วยของข้อมูลทางสถิติ แต่มีค่ากำลังสอง ดังนั้นค่าความแปรปรวนของชุดข้อมูลนี้คือ 57.2 ล้าน ²

➤ ดู: ส่วนเบี่ยงเบนมาตรฐานเสมือน

เครื่องคิดเลข Quasivariance

ป้อนข้อมูลทางสถิติที่กำหนดลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณความแปรปรวน ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

ความแปรปรวนและความแปรปรวน

ในที่สุด เราจะเห็นความแตกต่างระหว่างความแปรปรวนและความแปรปรวน เนื่องจากแม้จะมีชื่อที่คล้ายคลึงกัน แต่ก็ได้รับการคำนวณคล้ายกันมากเช่นกัน

ความแตกต่างระหว่างความแปรปรวนและความแปรปรวน คือตัวส่วนของสูตร ในการคำนวณความแปรปรวน คุณต้องหารด้วย n-1 อย่างไรก็ตาม ความแปรปรวนจะคำนวณโดยการหารด้วย n

ดังนั้น ความแปรปรวนและความแปรปรวนจึงมีความสัมพันธ์กันทางคณิตศาสตร์ เนื่องจากความแปรปรวนเทียบเท่ากับความแปรปรวนคูณด้วย n (จำนวนจุดข้อมูลทั้งหมด) แล้วหารด้วย n-1

$\sigma_{n-1}^2=\cfrac{n}{n-1}\cdot \sigma^2$

ดังนั้น สำหรับชุดข้อมูลเดียวกัน ค่าความแปรปรวนจะมากกว่าค่าความแปรปรวนเสมอ

➤ ดู: คุณสมบัติของการเบี่ยงเบน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม