ค่าสัมประสิทธิ์การตัดสินใจ (r กำลังสอง)
บทความนี้จะอธิบายว่าสัมประสิทธิ์การตัดสินใจ (หรือ R กำลังสอง) มีค่าเท่าใดในสถิติ ดังนั้นคุณจะได้เรียนรู้วิธีการคำนวณค่าสัมประสิทธิ์การกำหนดวิธีการตีความและนอกจากนี้เครื่องคิดเลขออนไลน์เพื่อคำนวณค่าสัมประสิทธิ์การกำหนดตัวอย่างข้อมูล
ค่าสัมประสิทธิ์การตัดสินใจ (R กำลังสอง) คืออะไร?
ค่าสัมประสิทธิ์การกำหนด ซึ่งมีสัญลักษณ์คือ R 2 ( R กำลังสอง ) เป็นสถิติที่วัดความพอดีของแบบจำลองการถดถอย ค่าสัมประสิทธิ์การกำหนดแสดงให้เห็นว่าแบบจำลองการถดถอยเหมาะสมกับชุดข้อมูลได้ดีเพียงใด กล่าวคือ เป็นตัวระบุเปอร์เซ็นต์ที่อธิบายโดยแบบจำลองการถดถอย
ดังนั้น ยิ่งค่าสัมประสิทธิ์การตัดสินใจสูง โมเดลการถดถอยก็จะยิ่งดีขึ้นเท่านั้น แม้ว่าจะไม่เป็นไปตามเงื่อนไขนี้เสมอไป แต่โดยหลักการแล้วเราสนใจที่จะกำหนดค่าสัมประสิทธิ์การตัดสินใจให้มากที่สุดเท่าที่จะเป็นไปได้ เราจะดูวิธีตีความค่าสัมประสิทธิ์การตัดสินใจด้านล่าง
สูตรการหาค่าสัมประสิทธิ์
ค่าสัมประสิทธิ์การกำหนดเท่ากับ 1 ลบอัตราส่วนระหว่างความแปรปรวนคงเหลือและความแปรปรวนของตัวแปรตาม ค่าสัมประสิทธิ์การกำหนดสามารถคำนวณได้โดยการลบหนึ่งลบผลรวมของกำลังสองออกจากส่วนที่เหลือมากกว่าผลรวมของกำลังสองทั้งหมด
ดังนั้น สูตรในการคำนวณค่าสัมประสิทธิ์การพิจารณา จึงเป็นดังนี้:

ทอง:
-

คือค่าสัมประสิทธิ์การตัดสินใจ
-
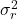
คือความแปรปรวนคงเหลือ
-

คือความแปรปรวนของตัวแปรตาม Y
-
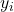
คือค่าของตัวแปรตามการสังเกต i
-
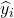
คือค่าประมาณโดยแบบจำลองการถดถอยสำหรับการสังเกต i
-

คือค่าเฉลี่ยของตัวแปรตามของการสังเกตทั้งหมด
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าสัมประสิทธิ์การตัดสินใจสำหรับชุดข้อมูลใดก็ได้
สำหรับกรณีของแบบจำลองการถดถอยเชิงเส้น ค่าสัมประสิทธิ์การกำหนดจะเท่ากับกำลังสองของ ค่าสัมประสิทธิ์สหสัมพันธ์ :
![]()
ทอง
![]()
คือ ความแปรปรวนร่วม ของตัวแปร X และ Y
![]()
และ
![]()
คือ ความแปรปรวน ของตัวแปรอิสระ X และตัวแปรตาม Y ตามลำดับ
เครื่องคำนวณค่าสัมประสิทธิ์การกำหนด
เสียบข้อมูลตัวอย่างลงในเครื่องคิดเลขด้านล่างเพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นอย่างง่าย และคำนวณค่าสัมประสิทธิ์การกำหนด คุณต้องแยกคู่ข้อมูลเพื่อให้ในกล่องแรกมีเพียงค่าของตัวแปรอิสระ X และในกล่องที่สองมีเพียงค่าของตัวแปรตาม Y
ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม
การตีความค่าสัมประสิทธิ์การตัดสินใจ
ในส่วนนี้ เราจะมาดูวิธีตีความค่าสัมประสิทธิ์การกำหนด เนื่องจากไม่มีประโยชน์ที่จะรู้ค่าของค่าสัมประสิทธิ์การกำหนด หากคุณไม่รู้ว่ามันหมายถึงอะไรในภายหลัง
ค่าสัมประสิทธิ์การกำหนดสามารถอยู่ในช่วงตั้งแต่ 0 ถึง 1 อย่างไรก็ตาม โดยปกติจะแสดงเป็นเปอร์เซ็นต์ ดังนั้นค่าต่ำสุดคือ 0% และค่าสูงสุดคือ 100%
เกี่ยวกับ การตีความค่าสัมประสิทธิ์การกำหนด ยิ่งค่ามีค่าสูงเท่าใด แบบจำลองการถดถอยจะอธิบายตัวอย่างข้อมูลได้ดีขึ้น ดังนั้น ยิ่งค่าสัมประสิทธิ์การกำหนดเข้าใกล้ 1 มากเท่าใด โมเดลก็จะยิ่งถูกปรับมากขึ้นเท่านั้น ในทางกลับกัน ยิ่งเข้าใกล้ 0 แบบจำลองการถดถอยที่สร้างขึ้นก็จะยิ่งมีความน่าเชื่อถือน้อยลงเท่านั้น
อย่างไรก็ตาม เมื่อเปรียบเทียบแบบจำลองการถดถอยสองแบบ แบบจำลองที่มีค่าสัมประสิทธิ์การถดถอยที่สูงกว่าไม่ได้ดีกว่าเสมอไป ตัวอย่างเช่น แบบจำลองการถดถอยอาจมีสัมประสิทธิ์การถดถอย R 2 = 100% เนื่องจากมีการเพิ่มตัวแปรอธิบายจำนวนมากลงในแบบจำลอง จึงสามารถอธิบายข้อสังเกตทั้งหมดได้อย่างสมบูรณ์แบบ แต่แบบจำลองนี้คาดการณ์ได้แย่มากสำหรับค่าใหม่ที่ไม่ได้ใช้ในการสร้างแบบจำลองการถดถอย
ควรจำไว้ว่าแบบจำลองการถดถอยที่ได้นั้นเป็นไปตามสมมติฐานก่อนหน้านี้ ดังนั้น แบบจำลองที่มีค่าสัมประสิทธิ์การกำหนดสูงมากจะไม่มีประโยชน์หากความแปรปรวนของค่าคงเหลือไม่คงที่ (homoscedasticity)
นอกจากนี้ ค่าสัมประสิทธิ์การกำหนดยังเป็นข้อจำกัดที่สำคัญ เนื่องจากไม่ได้ลงโทษการรวมตัวแปรอธิบายไว้ ตามตรรกะ ยิ่งตัวแปรที่มีคำอธิบายมากขึ้นในแบบจำลองการถดถอย แบบจำลองก็จะยิ่งซับซ้อนมากขึ้นเท่านั้น แต่ยิ่งอธิบายข้อมูลที่สังเกตได้ดีกว่า ดังนั้น ค่าสัมประสิทธิ์การตัดสินใจก็จะยิ่งสูงขึ้นเท่านั้น อย่างไรก็ตาม ค่าสัมประสิทธิ์การกำหนดที่ปรับแล้วจะพิจารณาจำนวนตัวแปรในแบบจำลอง (เราจะดูวิธีการคำนวณด้านล่าง)
โดยสรุป ค่าสัมประสิทธิ์การกำหนดมีประโยชน์อย่างมากในการวิเคราะห์แบบจำลองการถดถอย เนื่องจากช่วยให้เราทราบว่าแบบจำลองการถดถอยเหมาะสมกับชุดข้อมูลได้ดีเพียงใด อย่างไรก็ตาม ควรใช้เครื่องมืออื่นๆ เพื่อตรวจสอบแบบจำลองผลลัพธ์ เช่น กราฟทางสถิติ
ปรับค่าสัมประสิทธิ์การตัดสินใจแล้ว
ค่าสัมประสิทธิ์การกำหนดที่ปรับปรุง แล้ว หรือที่เรียกว่า ค่าสัมประสิทธิ์การกำหนดที่ปรับปรุงแล้ว จะวัดความพอดีของแบบจำลองการถดถอยโดยคำนึงถึงจำนวนตัวแปรอธิบายที่รวมอยู่ในแบบจำลอง
ความแตกต่างระหว่าง ค่าสัมประสิทธิ์การกำหนดและค่าสัมประสิทธิ์การกำหนดที่ปรับแล้ว คือ ค่าสัมประสิทธิ์การกำหนดจะวัดคุณภาพของการปรับโดยไม่คำนึงถึงจำนวนตัวแปร ในทางกลับกัน ค่าสัมประสิทธิ์การกำหนดที่ปรับแล้วจะวัดคุณภาพของการปรับ การลงโทษสำหรับตัวแปรที่เพิ่มแต่ละตัว
สูตรการคำนวณค่าสัมประสิทธิ์การตัดสินใจที่ปรับแล้วมีดังนี้:
![]()
ทอง:
-

คือค่าสัมประสิทธิ์การตัดสินใจที่ปรับแล้ว
-

คือค่าสัมประสิทธิ์การตัดสินใจ
-

คือขนาดตัวอย่าง
-

คือจำนวนตัวแปรอธิบายในแบบจำลองการถดถอย
ดังนั้นค่าสัมประสิทธิ์การกำหนดที่ปรับแล้วจะดีกว่าค่าสัมประสิทธิ์การกำหนดสำหรับการเปรียบเทียบแบบจำลองสองแบบที่แตกต่างกัน เนื่องจากแบบจำลองอาจมีจำนวนตัวแปรอธิบายที่แตกต่างกัน