เส้นถดถอย
บทความนี้จะอธิบายว่าเส้นถดถอยในสถิติคืออะไร ดังนั้น คุณจะพบวิธีคำนวณเส้นการถดถอยระหว่างตัวแปรสองตัว แบบฝึกหัดการแก้ปัญหา และเครื่องคำนวณออนไลน์เพิ่มเติมสำหรับคำนวณเส้นการถดถอยสำหรับตัวอย่างข้อมูลใดๆ
เส้นถดถอยคืออะไร?
ในสถิติ เส้นการถดถอย คือเส้นที่ได้รับจาก แบบจำลองการถดถอยเชิงเส้นอย่างง่าย แม่นยำยิ่งขึ้น เส้นการถดถอยคือเส้นที่เหมาะกับแผนภูมิกระจายมากที่สุด ดังนั้นจึงอธิบายชุดข้อมูลทางสถิติได้ดีที่สุด
ดังนั้น สมการเส้นถดถอยจึงสัมพันธ์ทางคณิตศาสตร์กับตัวแปรอิสระ X และตัวแปรตาม Y ของชุดข้อมูล แม้ว่าโดยทั่วไปเส้นการถดถอยจะไม่สามารถระบุค่าของการสังเกตแต่ละครั้งได้อย่างแม่นยำ แต่ก็สามารถให้ค่าประมาณได้

ดังที่คุณเห็นในกราฟก่อนหน้า เส้นการถดถอยช่วยให้เราเห็นแนวโน้มของชุดข้อมูลและประเภทของความสัมพันธ์ที่มีอยู่ระหว่างตัวแปรอิสระและตัวแปรตาม ด้านล่างนี้เราจะดูการใช้งานของเส้นการถดถอย
สูตรเส้นถดถอย
ตอนนี้เรารู้คำจำกัดความของเส้นการถดถอยแล้ว มาดูวิธีคำนวณสมการเส้นของตัวแบบการถดถอยเชิงเส้นกัน
เช่นเดียวกับเส้นใดๆ สมการของเส้นการถดถอยประกอบด้วยค่าคงที่ (b 0 ) และความชัน (b 1 ):
![]()
ดังนั้น สูตรในการคำนวณค่าสัมประสิทธิ์ของเส้นการถดถอยเชิงเส้น จึงเป็นดังนี้:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6dc6f56cacf0a233977c358d6a62fca8_l3.png)
ทอง:
-
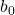
คือค่าคงที่ของเส้นถดถอย
-
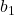
คือความชันของเส้นถดถอย
-

คือค่าของตัวแปรอิสระ X ของข้อมูล i
-

คือค่าของตัวแปรตาม Y ของข้อมูล i
-

คือค่าเฉลี่ยของค่าของตัวแปรอิสระ
-

คือค่าเฉลี่ยของค่าของตัวแปรตาม Y
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณเส้นถดถอยสำหรับชุดข้อมูลใดก็ได้
ตัวอย่างที่เป็นรูปธรรมของเส้นถดถอย
หากต้องการสำรวจแนวคิดของเส้นการถดถอยเพิ่มเติม ด้านล่างนี้คือตัวอย่างการทำงานของวิธีสร้างเส้นการถดถอย
- หลังจากสอบสถิติ นักเรียน 5 คนถูกถามว่าใช้เวลาเรียนกี่ชั่วโมง ข้อมูลแสดงไว้ในตารางด้านล่าง คำนวณเส้นการถดถอยจากข้อมูลทางสถิติที่รวบรวมมาเพื่อเชื่อมโยงชั่วโมงเรียนกับเกรดที่ได้รับเชิงเส้นตรง ต่อไปให้พิจารณาว่านักเรียนที่เรียน 8 ชั่วโมงจะได้เกรดเท่าใด

ในการค้นหาเส้นการถดถอยสำหรับข้อมูลตัวอย่าง เราต้องกำหนดค่าสัมประสิทธิ์ b 0 และ b 1 ของสมการ และในการทำเช่นนี้ เราจำเป็นต้องใช้สูตรที่เห็นในส่วนด้านบน
อย่างไรก็ตาม ในการใช้สูตรสำหรับเส้นการถดถอยเชิงเส้น เราต้องคำนวณค่าเฉลี่ยของตัวแปรอิสระและค่าเฉลี่ยของตัวแปรตามก่อน:
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
ตอนนี้เรารู้ค่าเฉลี่ยของตัวแปรแล้ว เราก็คำนวณค่าสัมประสิทธิ์ b 1 ของแบบจำลองโดยใช้สูตรที่เกี่ยวข้อง:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
สุดท้ายเราคำนวณค่าสัมประสิทธิ์ b 0 ของแบบจำลองโดยใช้สูตรที่เกี่ยวข้อง:
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
กล่าวโดยสรุป สมการของเส้นการถดถอยเชิงเส้นของปัญหามีดังนี้
![]()
ด้านล่างนี้ คุณจะเห็นการแสดงข้อมูลตัวอย่างแบบกราฟิกตลอดจนเส้นตรงของแบบจำลองการถดถอยเชิงเส้นอย่างง่าย:

เมื่อเราคำนวณเส้นการถดถอยแล้ว เพื่อทำนายเกรดที่นักเรียนที่เรียน 8 ชั่วโมงจะได้รับ ให้แทนค่านี้ลงในสมการของเส้นการถดถอยที่ได้รับ:
![]()
ดังนั้น ตามแบบจำลองการถดถอยเชิงเส้น หากนักเรียนเรียนเป็นเวลา 8 ชั่วโมง เขาจะได้คะแนนสอบ 5.56
เส้นถดถอยใช้ทำอะไร?
โดยหลักแล้ว เส้นการถดถอยมีประโยชน์สองประการ: เส้นการถดถอยใช้เพื่อกำหนดประเภทของความสัมพันธ์ที่มีอยู่ระหว่างตัวแปรสองตัว และในทางกลับกัน เส้นการถดถอยยังทำให้คุณสามารถคาดการณ์เกี่ยวกับค่าของการสังเกตใหม่ได้
ความชันของเส้นถดถอยบอกเราว่าความ สัมพันธ์ ระหว่างตัวแปรอิสระและตัวแปรตามเป็นอย่างไร ถ้าความชันเป็นบวก หมายความว่าตัวแปรตามเป็นสัดส่วนโดยตรงกับตัวแปรอิสระ ในขณะที่ถ้าความชันเป็นลบ ก็แสดงว่าตัวแปรนั้นมีสัดส่วนผกผัน ท้ายที่สุด หากค่าสัมประสิทธิ์ความชันใกล้กับศูนย์มาก นั่นหมายความว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นอ่อนมาก
นอกจากนี้ หากทราบสมการของเส้นการถดถอย ค่าของตัวแปรตามสามารถทำนายค่าใหม่ของตัวแปรอิสระได้ ดังที่เราทำในตัวอย่างข้างต้น ดังนั้น ยิ่งมีการปรับเส้นการถดถอยให้ดีขึ้นเท่าใด การคาดการณ์ก็จะยิ่งดีขึ้นเท่านั้น
เครื่องคิดเลขเส้นถดถอย
ใส่ตัวอย่างข้อมูลลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณเส้นถดถอยระหว่างตัวแปรทั้งสอง คุณต้องแยกคู่ข้อมูลเพื่อให้ในกล่องแรกมีเพียงค่าของตัวแปรอิสระ X และในกล่องที่สองมีเพียงค่าของตัวแปรตาม Y
ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม