วิธีการดำเนินการ loess regression ใน r (พร้อมตัวอย่าง)
การถดถอยแบบ LOESS ซึ่งบางครั้งเรียกว่าการถดถอยแบบเฉพาะที่ เป็นวิธีการที่ใช้การปรับเฉพาะแบบเพื่อให้พอดีกับแบบจำลองการถดถอยกับชุดข้อมูล
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการดำเนินการถดถอย LOESS ใน R
ขั้นตอนที่ 1: สร้างข้อมูล
ขั้นแรก เรามาสร้าง data frame ต่อไปนี้ใน R:
#view DataFrame df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14), y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27)) #view first six rows of data frame head(df) xy 1 1 1 2 2 4 3 3 7 4 4 13 5 5 19 6 6 24
ขั้นตอนที่ 2: ติดตั้งโมเดลการถดถอย LOESS หลายตัว
เราสามารถใช้ฟังก์ชัน loess() เพื่อให้พอดีกับโมเดลการถดถอย LOESS หลายตัวกับชุดข้อมูลนี้ โดยใช้ค่าที่แตกต่างกันสำหรับพารามิเตอร์ span :
#fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50)
loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75)
loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90)
#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')
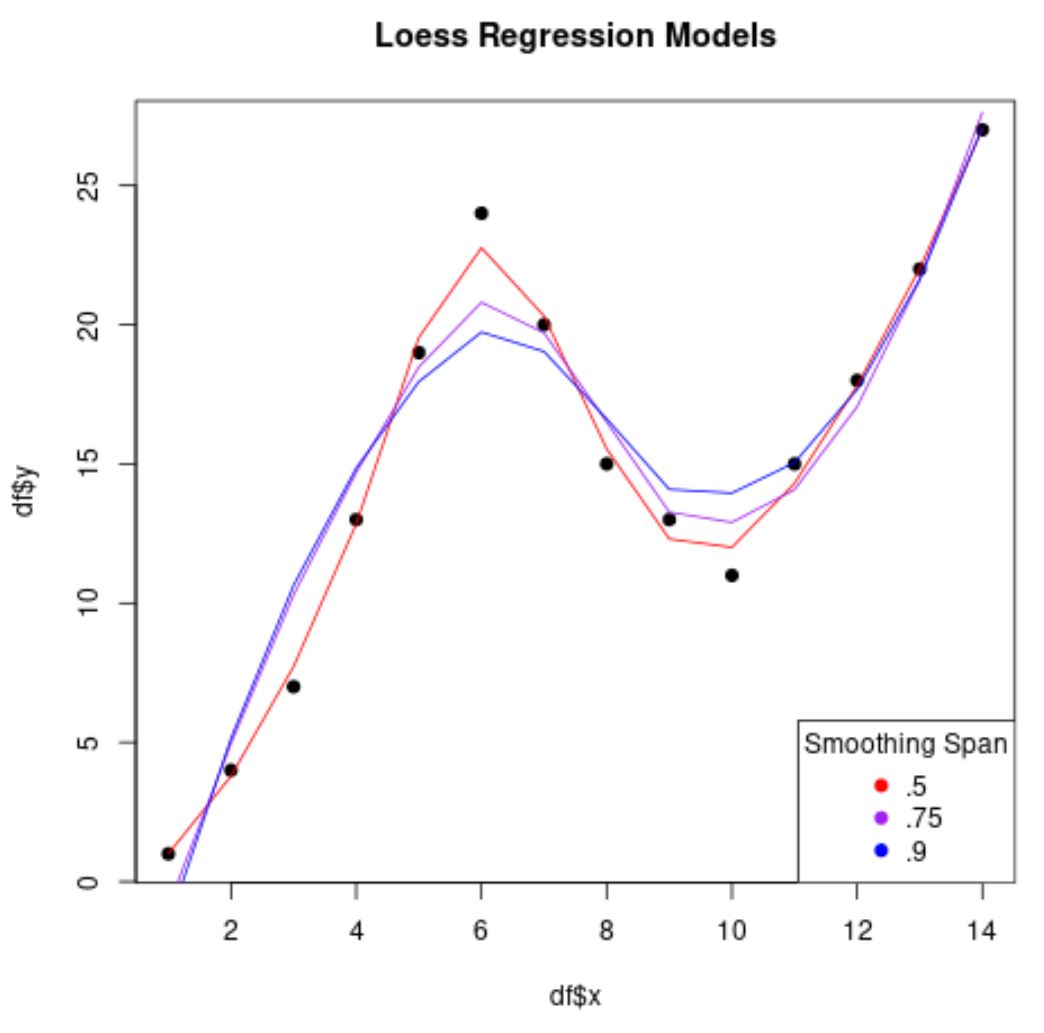
โปรดทราบว่ายิ่งเราใช้ค่า span ต่ำ โมเดลการถดถอยก็จะมีความ “ราบรื่น” น้อยลง และโมเดลจะพยายามปรับให้พอดีกับจุดข้อมูลมากขึ้นเท่านั้น
ขั้นตอนที่ 3: ใช้ K-Fold Cross-Validation เพื่อค้นหาโมเดลที่ดีที่สุด
เพื่อค้นหาค่า ขอบเขต ที่เหมาะสมที่สุดที่จะใช้ เราสามารถดำเนิน การตรวจสอบข้าม k-fold โดยใช้ฟังก์ชันในแพ็คเกจ คาเร็ต :
library (caret)
#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )
#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)
#print results of k-fold cross-validation
print (model)
14 samples
1 predictor
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 12, 11, 11, 11, 11
Resampling results across tuning parameters:
span RMSE Rsquared MAE
0.5 10.148315 0.9570137 6.467066
0.6 7.854113 0.9350278 5.343473
0.7 6.113610 0.8150066 4.769545
0.8 17.814105 0.8202561 11.875943
0.9 26.705626 0.7384931 17.304833
Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.
เราจะเห็นว่าค่า สแปน ที่สร้างค่าต่ำสุดสำหรับ ข้อผิดพลาดรูตค่าเฉลี่ยกำลัง สอง (RMSE) คือ 0.7
ดังนั้น สำหรับโมเดลการถดถอย LOESS สุดท้าย เราจะเลือกใช้ค่า 0.7 สำหรับอาร์กิวเมนต์ span ในฟังก์ชัน loess()
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับแบบจำลองการถดถอยใน R:
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยโลจิสติกใน R
วิธีดำเนินการถดถอยเชิงปริมาณใน R
วิธีดำเนินการถดถอยถ่วงน้ำหนักใน R