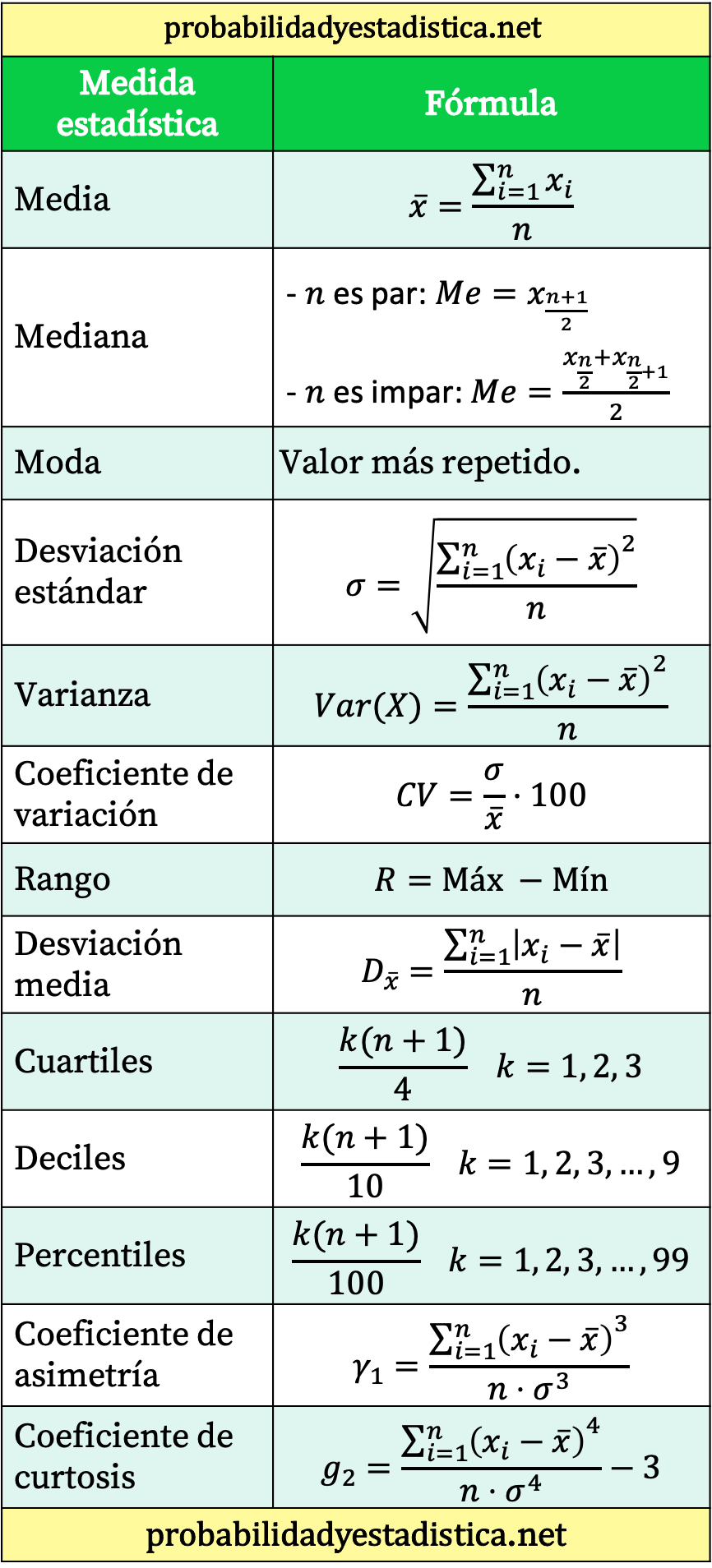
สูตรทางสถิติ

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 1, 2023 สถิติ 0 ความคิดเห็น

ที่นี่คุณจะได้พบกับสูตรทางสถิติหลัก นอกจากนี้ เรายังให้คุณลิงก์ไปยังบทความของเรา ซึ่งคุณสามารถดูตัวอย่างการใช้สูตรทางสถิติแต่ละสูตรได้ นอกจากนี้ คุณยังสามารถใช้เครื่องคิดเลขออนไลน์ได้ เพื่อจะได้ไม่ต้องคำนวณและรู้ผลลัพธ์ของสูตรโดยตรง

สูตรการวัดทางสถิติของแนวโน้มส่วนกลาง

ครึ่ง

ในการคำนวณค่า เฉลี่ย ให้บวกค่าทั้งหมดแล้วหารด้วยจำนวนข้อมูลทั้งหมด สูตรสำหรับค่าเฉลี่ยจึงเป็นดังนี้:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

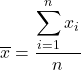
ในทางสถิติ ค่าเฉลี่ยเรียกอีกอย่างว่า ค่าเฉลี่ยเลขคณิต หรือ ค่าเฉลี่ย

➤ ดู: เครื่องคำนวณค่าเฉลี่ยเลขคณิต

ค่ามัธยฐาน

ค่ามัธยฐาน คือค่ากลางของข้อมูลทั้งหมดโดยเรียงลำดับจากน้อยไปหามาก กล่าวอีกนัยหนึ่ง ค่ามัธยฐานจะแบ่งชุดข้อมูลที่เรียงลำดับออกเป็นสองส่วนเท่าๆ กัน

การคำนวณค่ามัธยฐานขึ้นอยู่กับว่าจำนวนข้อมูลทั้งหมดเป็นเลขคู่หรือคี่:

หากจำนวนข้อมูลทั้งหมดเป็นเลข คี่ ค่ามัธยฐานจะเป็นค่าที่อยู่ตรงกลางข้อมูล กล่าวคือค่าที่อยู่ในตำแหน่ง (n+1)/2 ของข้อมูลที่เรียงลำดับ

$Me=x_{\frac{n+1}{2}$

หากจำนวนจุดข้อมูลทั้งหมดเป็น เลขคู่ ค่ามัธยฐานจะเป็นค่าเฉลี่ยของจุดข้อมูล 2 จุดที่อยู่ตรงกลาง กล่าวคือค่าเฉลี่ยเลขคณิตของค่าที่พบในตำแหน่ง n/2 และ n/2+1 ของข้อมูลที่เรียงลำดับ

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

ทอง

$n$

คือจำนวนข้อมูลทั้งหมดในตัวอย่าง และสัญลักษณ์ Me หมายถึงค่ามัธยฐาน

➤ ดู: เครื่องคิดเลขค่ามัธยฐาน

แฟชั่น

ในสถิติ โหมด คือค่าในชุดข้อมูลที่มีความถี่สัมบูรณ์สูงสุด กล่าวคือ โหมดคือค่าที่ซ้ำกันมากที่สุดในชุดข้อมูล

ดังนั้นจึงไม่มีสูตรเฉพาะสำหรับโหมด แต่ในการคำนวณโหมดของชุดข้อมูลทางสถิติ เพียงนับจำนวนครั้งที่องค์ประกอบข้อมูลแต่ละรายการปรากฏในตัวอย่าง และข้อมูลที่ซ้ำกันมากที่สุดจะเป็นโหมด

โหมดนี้อาจกล่าวได้ว่าเป็น โหมดทางสถิติ หรือ ค่ากิริยา ช่วย

➤ ดูที่: เครื่องคิดเลขแฟชั่น

สูตรสำหรับการวัดค่าทางสถิติของการกระจายตัว

ส่วนเบี่ยงเบนมาตรฐาน

ค่าเบี่ยงเบนมาตรฐานหรือที่เรียกว่าค่าเบี่ยงเบนมาตรฐาน เท่ากับรากที่สองของผลรวมของกำลังสองของค่าเบี่ยงเบนของชุดข้อมูลหารด้วยจำนวนการสังเกตทั้งหมด

ดังนั้น สูตรสำหรับส่วนเบี่ยงเบนมาตรฐาน คือ:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ ดู: เครื่องคำนวณค่าเบี่ยงเบนมาตรฐาน

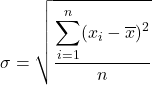
ความแปรปรวน

ความแปรปรวน เท่ากับผลรวมของกำลังสองของส่วนที่เหลือต่อจำนวนการสังเกตทั้งหมด สูตรสำหรับตัวชี้วัดทางสถิตินี้จึงเป็นดังนี้:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

ทอง:

$X$

คือตัวแปรสุ่มที่คุณต้องการคำนวณความแปรปรวน
$x_i$

คือค่าข้อมูล

$i$

.
$n$

คือจำนวนการสังเกตทั้งหมด
$\overline{X}$

คือค่าเฉลี่ยของตัวแปรสุ่ม

$X$

.

➤ ดู: เครื่องคิดเลข Gap

ค่าสัมประสิทธิ์ของการแปรผัน

ในสถิติ ค่าสัมประสิทธิ์ของการแปรผัน คือการวัดการกระจายตัวที่ใช้ในการกำหนดการกระจายตัวของชุดข้อมูลที่สัมพันธ์กับค่าเฉลี่ย ค่าสัมประสิทธิ์ของการแปรผันคำนวณโดยการหารค่าเบี่ยงเบนมาตรฐานของข้อมูลด้วยค่าเฉลี่ย จากนั้นคูณด้วย 100 เพื่อแสดงค่าเป็นเปอร์เซ็นต์

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ ดู: ค่าสัมประสิทธิ์ของเครื่องคิดเลขความแปรผัน

เรียบร้อย

ช่วงทางสถิติ คือการวัดการกระจายตัวที่ระบุความแตกต่างระหว่างค่าสูงสุดและค่าต่ำสุดของข้อมูลในตัวอย่าง ดังนั้น ในการคำนวณขอบเขตของประชากรหรือตัวอย่างทางสถิติ ค่าสูงสุดจะต้องลบออกจากค่าต่ำสุด

$R=\text{M\'ax}-\text{M\'in}$

➤ ดู ตัวอย่างช่วงทางสถิติ

พิสัยระหว่างควอไทล์

ช่วงระหว่างควอร์ไทล์ หรือที่เรียกว่า ช่วงระหว่างควอไทล์ เป็นหน่วยวัดการกระจายตัวทางสถิติที่ระบุความแตกต่างระหว่างควอร์ไทล์ที่ 3 และควอไทล์ที่ 1

ดังนั้น ในการคำนวณช่วงระหว่างควอร์ไทล์ของชุดข้อมูลทางสถิติ คุณต้องค้นหาควอไทล์ที่สามและควอไทล์ที่หนึ่งก่อนแล้วจึงลบออก

$IQR=Q_3-Q_1$

➤ ดู: เครื่องคำนวณช่วงระหว่างควอไทล์

ความแตกต่างปานกลาง

ค่าเฉลี่ยส่วนเบี่ยงเบน หรือที่เรียกว่า ค่าเฉลี่ยส่วนเบี่ยงเบนสัมบูรณ์ คือค่าเฉลี่ยของการเบี่ยงเบนสัมบูรณ์ ค่าเบี่ยงเบนเฉลี่ยจึงเท่ากับผลรวมของการเบี่ยงเบนของแต่ละรายการข้อมูลจากค่าเฉลี่ยเลขคณิตหารด้วยจำนวนรายการข้อมูลทั้งหมด

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ ดู: เครื่องคำนวณค่าเบี่ยงเบนเฉลี่ย

สูตรสำหรับการวัดตำแหน่งทางสถิติ

ควอไทล์

ในสถิติ ควอไทล์ คือค่าสามค่าที่แบ่งชุดข้อมูลที่เรียงลำดับออกเป็นสี่ส่วนเท่าๆ กัน ดังนั้นควอร์ไทล์ที่หนึ่ง สอง และสามจึงคิดเป็น 25%, 50% และ 75% ของข้อมูลทางสถิติทั้งหมดตามลำดับ

ควอไทล์แสดงด้วยตัวพิมพ์ใหญ่ Q และดัชนีควอร์ไทล์ ดังนั้นควอไทล์แรกคือ Q ₁ ควอไทล์ที่สองคือ Q ₂ และควอร์ไทล์ที่สามคือ Q ₃

สูตรควอไทล์ คือ:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

โปรดทราบ: สูตรนี้บอกเราถึงตำแหน่งของควอไทล์ ไม่ใช่ค่าของควอไทล์ ควอไทล์จะเป็นข้อมูลที่อยู่ในตำแหน่งที่ได้จากสูตร

อย่างไรก็ตาม บางครั้งผลลัพธ์ของสูตรนี้จะทำให้เราได้เลขทศนิยม ดังนั้นเราจึงต้องแยกแยะสองกรณีขึ้นอยู่กับว่าผลลัพธ์เป็นเลขทศนิยมหรือไม่:

หากผลลัพธ์ของสูตรเป็น ตัวเลขที่ไม่มีทศนิยม ควอ ไทล์คือข้อมูลที่อยู่ในตำแหน่งที่ระบุในสูตรด้านบน
หากผลลัพธ์ของสูตรเป็น ตัวเลขที่มีส่วนทศนิยม ค่าควอไทล์จะคำนวณโดยใช้สูตรต่อไปนี้:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

โดยที่ x _i และ x _i+1 คือตัวเลขของตำแหน่งระหว่างตำแหน่งที่มีตัวเลขที่ได้จากสูตรแรกอยู่ และ d คือส่วนทศนิยมของตัวเลขที่ได้จากสูตรแรก

➤ ดู: เครื่องคำนวณควอไทล์

เดซิล

ในสถิติ deciles คือค่าเก้าค่าที่แบ่งชุดข้อมูลที่เรียงลำดับออกเป็นสิบส่วนเท่า ๆ กัน ดังนั้นเดไซล์ที่หนึ่ง สอง สาม… แทน 10%, 20%, 30%,… ของกลุ่มตัวอย่างหรือประชากร

เดไซล์แสดงด้วยอักษรตัวใหญ่ D และดัชนีเดไซล์ กล่าวคือ เดไซล์ตัวแรกคือ D ₁ เดไซล์ตัวที่สองคือ D ₂ เดไซล์ตัวที่สามคือ D ₃ เป็นต้น

สูตรเดซิล มีดังนี้:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

โปรดทราบ: สูตรนี้บอกเราถึงตำแหน่งของเดไซล์ ไม่ใช่ค่าของเดไซล์ เดไซล์จะเป็นข้อมูลที่อยู่ในตำแหน่งที่ได้จากสูตร

อย่างไรก็ตาม บางครั้งผลลัพธ์ของสูตรนี้จะให้ค่าเป็นเลขทศนิยม ดังนั้น เราจึงต้องแยกความแตกต่างออกเป็น 2 กรณี ขึ้นอยู่กับว่าผลลัพธ์เป็นเลขทศนิยมหรือไม่:

หากผลลัพธ์ของสูตรเป็น ตัวเลขที่ไม่มีทศนิยม เดไซล์คือข้อมูลที่อยู่ในตำแหน่งที่ระบุในสูตรด้านบน
หากผลลัพธ์ของสูตรเป็น ตัวเลขที่มีส่วนทศนิยม ค่าเดไซล์จะคำนวณโดยใช้สูตรต่อไปนี้:

$D=x_i+d\cdot (x_{i+1}-x_i)$

➤ ดู: เครื่องคิดเลข Decile

เปอร์เซ็นไทล์

ในทางสถิติ เปอร์เซ็นไทล์ คือค่าที่แบ่งชุดข้อมูลที่เรียงลำดับออกเป็นหนึ่งร้อยส่วนเท่าๆ กัน ดังนั้น เปอร์เซ็นไทล์จะระบุค่าที่ต่ำกว่าซึ่งเปอร์เซ็นต์ของชุดข้อมูลอยู่

เปอร์เซ็นไทล์แสดงด้วยอักษรตัวใหญ่ P และดัชนีเปอร์เซ็นไทล์ นั่นคือ เปอร์เซ็นไทล์แรกคือ P ₁ เปอร์เซ็นไทล์ที่ 40 คือ P ₄₀ เปอร์เซ็นไทล์ที่ 79 คือ P ₇₉ เป็นต้น

สูตรเปอร์เซ็นไทล์ คือ:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

โปรดทราบ: สูตรนี้บอกเราถึงตำแหน่งของเปอร์เซ็นไทล์ แต่ไม่ใช่ค่าของมัน เปอร์เซ็นไทล์จะเป็นข้อมูลที่อยู่ในตำแหน่งที่ได้จากสูตร

หากผลลัพธ์ของสูตรเป็น ตัวเลขที่ไม่มีส่วนทศนิยม เปอร์เซ็นไทล์จะสอดคล้องกับข้อมูลที่อยู่ในตำแหน่งที่ระบุในสูตรด้านบน
หากผลลัพธ์ของสูตรเป็น ตัวเลขที่มีส่วนทศนิยม ค่าเปอร์เซ็นไทล์ที่แน่นอนจะคำนวณโดยใช้สูตรต่อไปนี้:

$P=x_i+d\cdot (x_{i+1}-x_i)$

➤ ดู: เครื่องคำนวณเปอร์เซ็นต์

สูตรการวัดรูปร่างทางสถิติ

ค่าสัมประสิทธิ์ความไม่สมดุล

ค่าสัมประสิทธิ์ความเบ้หรือดัชนีความเบ้เป็นค่าสัมประสิทธิ์ทางสถิติที่ใช้ในการกำหนดความเบ้ของการแจกแจง ดังนั้น ด้วยการคำนวณค่าสัมประสิทธิ์ความไม่สมมาตร คุณสามารถทราบประเภทของความไม่สมมาตรของการแจกแจงได้โดยไม่ต้องแสดงค่าเป็นกราฟิก

สูตรสำหรับค่าสัมประสิทธิ์ความไม่สมมาตร มีดังนี้:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

ในทำนองเดียวกัน สามารถใช้สูตรใดสูตรหนึ่งจากสองสูตรต่อไปนี้ในการคำนวณค่าสัมประสิทธิ์ความไม่สมมาตรของฟิชเชอร์ได้:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

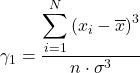
ทอง

$E$

คือความคาดหวังทางคณิตศาสตร์

$\overline{x}$

ค่าเฉลี่ยเลขคณิต

$\sigma$

ส่วนเบี่ยงเบนมาตรฐานและ

$n$

จำนวนข้อมูลทั้งหมด

➤ ดู: สัมประสิทธิ์ความไม่สมมาตร

ค่าสัมประสิทธิ์ความโด่ง

Kurtosis หรือที่เรียกว่าความคม บ่งชี้ว่าการกระจายตัวมีความเข้มข้นเพียงใดรอบๆ ค่าเฉลี่ย กล่าวอีกนัยหนึ่ง ความโด่งบ่งชี้ว่าการกระจายตัวสูงชันหรือราบเรียบ โดยเฉพาะอย่างยิ่ง ยิ่งการกระจายตัวมีความโด่งมากเท่าใด ความชันก็จะยิ่งชันมากขึ้นเท่านั้น

สูตรสำหรับค่าสัมประสิทธิ์ความโด่ง มีดังนี้:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

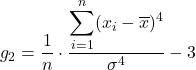
ทอง

$x_i$

คือค่าที่สอดคล้องกับการสังเกต

$i$