วิธีใช้วิธีกำลังสองน้อยที่สุดใน r
วิธีกำลังสองน้อยที่สุด คือวิธีที่เราสามารถใช้เพื่อค้นหาเส้นถดถอยที่เหมาะกับชุดข้อมูลที่กำหนดมากที่สุด
หากต้องการใช้วิธีการกำลังสองน้อยที่สุดเพื่อให้พอดีกับเส้นการถดถอยใน R เราสามารถใช้ฟังก์ชัน lm()
ฟังก์ชันนี้ใช้ไวยากรณ์พื้นฐานต่อไปนี้:
model <- lm(response ~ predictor, data=df)
ตัวอย่างต่อไปนี้แสดงวิธีการใช้ฟังก์ชันนี้ใน R
ตัวอย่าง: วิธีกำลังสองน้อยที่สุดใน R
สมมติว่าเรามีกรอบข้อมูลต่อไปนี้ใน R ที่แสดงจำนวนชั่วโมงที่เรียนและคะแนนสอบที่สอดคล้องกันของนักเรียน 15 คนในชั้นเรียน:
#create data frame df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of data frame head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
เราสามารถใช้ฟังก์ชัน lm() เพื่อใช้วิธีการกำลังสองน้อยที่สุดเพื่อให้พอดีกับเส้นการถดถอยกับข้อมูลนี้:
#use method of least squares to fit regression line model <- lm(score ~ hours, data=df) #view regression model summary summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
จากค่าในคอลัมน์ผลลัพธ์ โดย ประมาณ เราสามารถเขียนบรรทัดการถดถอยที่พอดีต่อไปนี้:
คะแนนสอบ = 65.334 + 1.982 (ชั่วโมง)
ต่อไปนี้คือวิธีตีความแต่ละค่าสัมประสิทธิ์ในโมเดล:
- Intercept : สำหรับนักศึกษาที่เรียน 0 ชั่วโมง คะแนนสอบที่คาดหวังคือ 65.334
- ชั่วโมง : สำหรับแต่ละชั่วโมงที่เรียนเพิ่มเติม คะแนนสอบที่คาดหวังจะเพิ่มขึ้น 1,982
เราสามารถใช้สมการนี้เพื่อประมาณเกรดการสอบที่นักเรียนจะได้รับตามชั่วโมงเรียน
ตัวอย่างเช่น หากนักเรียนเรียนเป็นเวลา 5 ชั่วโมง เราจะประมาณว่าคะแนนสอบของพวกเขาจะเท่ากับ 75.244:
คะแนนสอบ = 65.334 + 1.982(5) = 75.244
สุดท้ายนี้ เราสามารถสร้างแผนภาพกระจายของข้อมูลต้นฉบับโดยมีเส้นถดถอยที่พอดีวางทับบนโครงเรื่อง:
#create scatter plot of data plot(df$hours, df$score, pch=16, col=' steelblue ') #add fitted regression line to scatter plot abline(model)
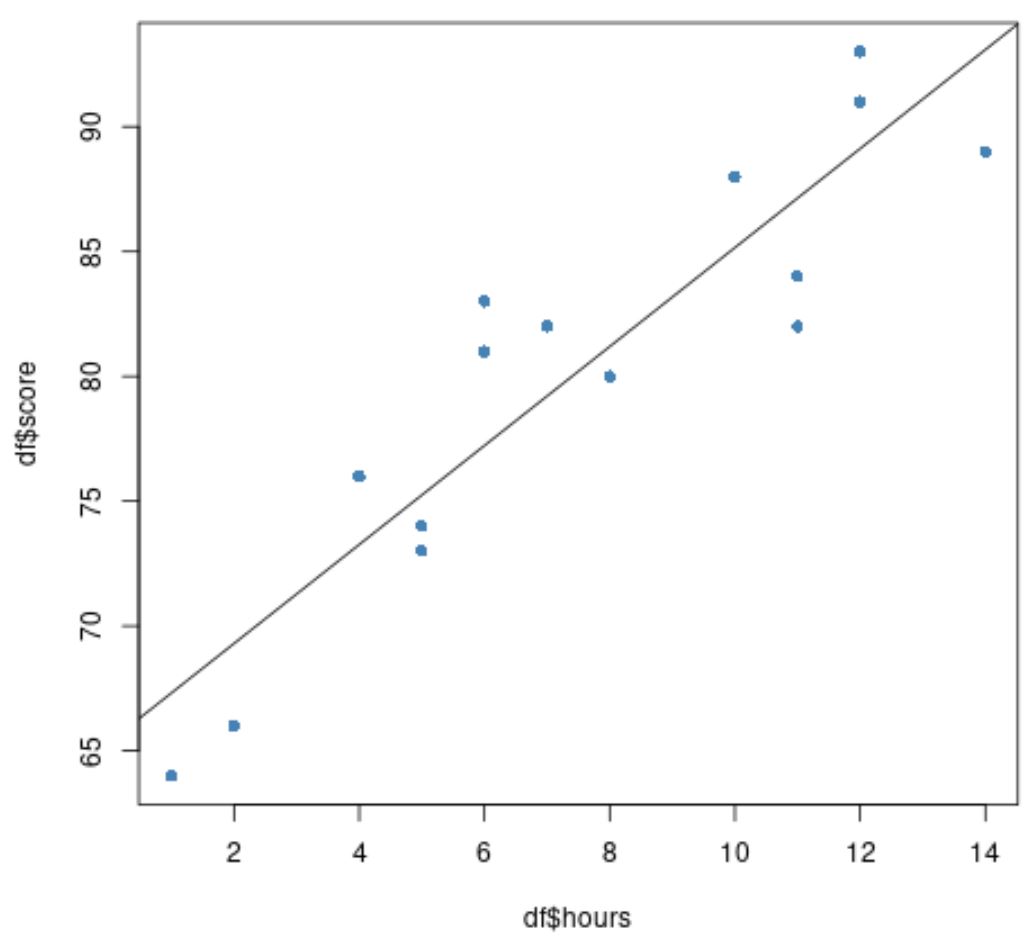
วงกลมสีน้ำเงินแสดงถึงข้อมูล และเส้นสีดำแสดงถึงเส้นถดถอยพอดี
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:
วิธีสร้างพล็อตที่เหลือใน R
วิธีทดสอบ multicollinearity ใน R
วิธีการปรับเส้นโค้งใน R