วิธีใช้วิธี elbow ใน python เพื่อค้นหาคลัสเตอร์ที่เหมาะสมที่สุด

อัลกอริธึมการจัดกลุ่มที่ใช้กันทั่วไปอย่างหนึ่งใน การเรียนรู้ของเครื่อง เรียกว่า การจัดกลุ่มแบบเคมีน

การจัดกลุ่มแบบเคมีนเป็นเทคนิคที่เราวางแต่ละการสังเกตจากชุดข้อมูลลงในคลัสเตอร์ K กลุ่มใดกลุ่มหนึ่ง

เป้าหมายสุดท้ายคือการมีกระจุกดาว K ซึ่งการสังเกตภายในแต่ละกระจุกจะค่อนข้างคล้ายกัน ในขณะที่การสังเกตในกลุ่มต่าง ๆ จะค่อนข้างแตกต่างกัน

เมื่อทำการจัดกลุ่มแบบเคมีน ขั้นตอนแรกคือการเลือกค่าสำหรับ K ซึ่งเป็นจำนวนคลัสเตอร์ที่เราต้องการใส่การสังเกตลงไป

วิธีหนึ่งที่พบบ่อยที่สุดในการเลือกค่าสำหรับ K เรียกว่า วิธีข้อศอก ซึ่งเกี่ยวข้องกับการสร้างพล็อตด้วยจำนวนกลุ่มบนแกน x และผลรวมเป็นผลรวมของกำลังสองบนแกน y จากนั้นระบุ โดยที่ “เข่า” หรือการเลี้ยวปรากฏในโครงเรื่อง

จุดบนแกน x ที่ “หัวเข่า” เกิดขึ้นบอกเราถึงจำนวนคลัสเตอร์ที่เหมาะสมที่สุดที่จะใช้ในอัลกอริทึมการจัดกลุ่มแบบเคมีน

ตัวอย่างต่อไปนี้แสดงวิธีการใช้วิธีข้อศอกใน Python

ขั้นตอนที่ 1: นำเข้าโมดูลที่จำเป็น

ขั้นแรก เราจะนำเข้าโมดูลทั้งหมดที่เราจำเป็นต้องใช้ในการทำคลัสเตอร์แบบเคมีน:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

ขั้นตอนที่ 2: สร้าง DataFrame

ต่อไป เราจะสร้าง DataFrame ที่มีตัวแปรสามตัวสำหรับผู้เล่นบาสเก็ตบอล 20 คน:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

ขั้นตอนที่ 3: ใช้วิธีข้อศอกเพื่อค้นหาจำนวนคลัสเตอร์ที่เหมาะสมที่สุด

สมมติว่าเราต้องการใช้การจัดกลุ่มเคมีนเพื่อจัดกลุ่มนักแสดงที่คล้ายกันเข้าด้วยกันโดยยึดตามตัวชี้วัดทั้งสามนี้

หากต้องการดำเนินการจัดกลุ่มแบบเคมีนใน Python เราสามารถใช้ฟังก์ชัน KMeans จากโมดูล sklearn ได้

อาร์กิวเมนต์ที่สำคัญที่สุดสำหรับฟังก์ชันนี้คือ n_clusters ซึ่งระบุจำนวนคลัสเตอร์ที่จะวางการสังเกต

ในการกำหนดจำนวนคลัสเตอร์ที่เหมาะสมที่สุด เราจะสร้างกราฟที่แสดงจำนวนคลัสเตอร์ตลอดจน SSE (ผลรวมของข้อผิดพลาดกำลังสอง) ของแบบจำลอง

จากนั้นเราจะมองหา “เข่า” ซึ่งผลรวมของช่องสี่เหลี่ยมเริ่ม “โค้งงอ” หรือทรงตัว จุดนี้แสดงถึงจำนวนคลัสเตอร์ที่เหมาะสมที่สุด

รหัสต่อไปนี้แสดงวิธีสร้างพล็อตประเภทนี้ซึ่งแสดงจำนวนคลัสเตอร์บนแกน x และ SSE บนแกน y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

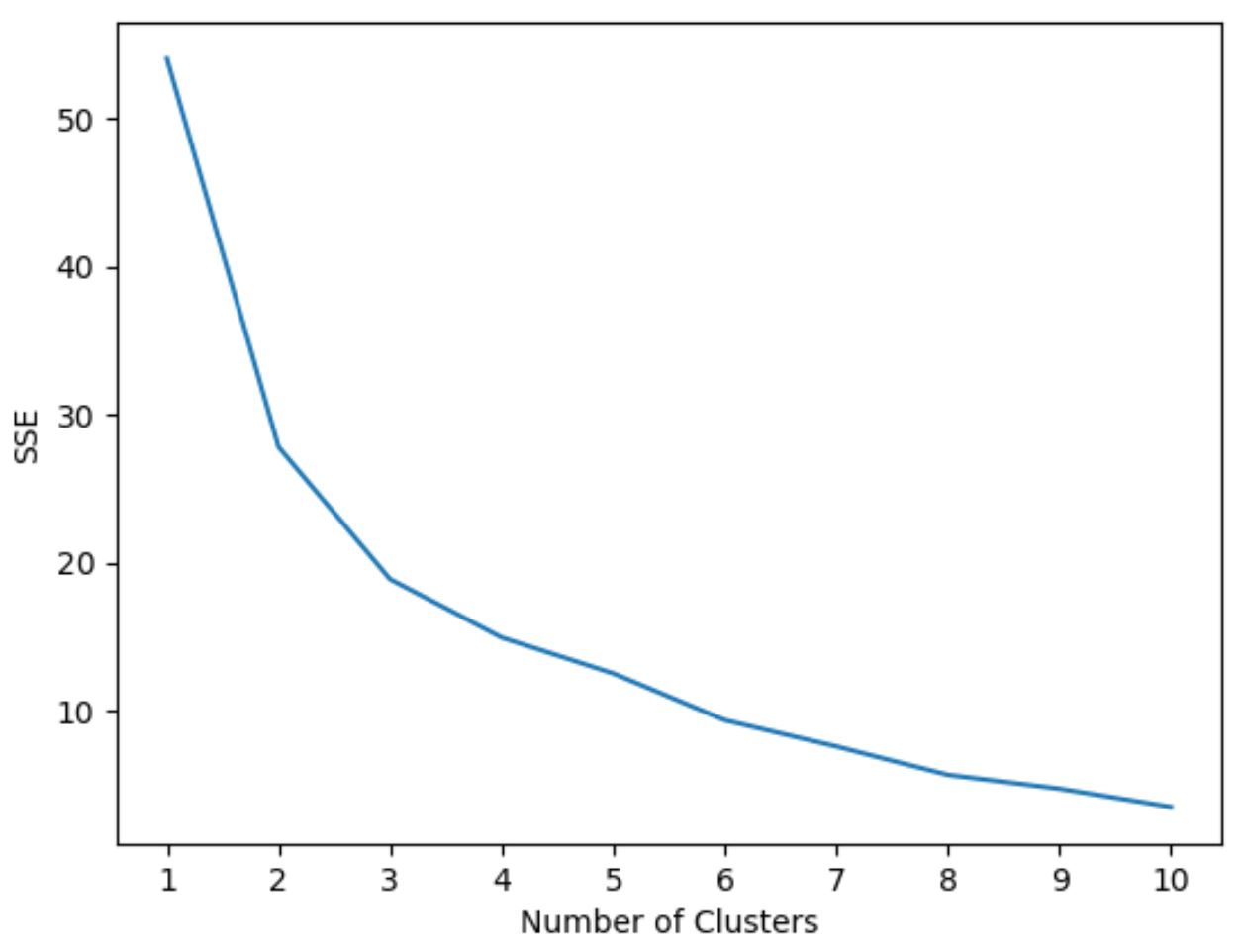
ในกราฟนี้ปรากฏว่ามีการงอหรือ “เข่า” ที่ k = 3 กลุ่ม

ดังนั้น เราจะใช้ 3 คลัสเตอร์เมื่อปรับโมเดลการจัดกลุ่มเคมีนของเราให้เหมาะสมในขั้นตอนถัดไป

ขั้นตอนที่ 4: ดำเนินการจัดกลุ่ม K-Means ด้วย Optimal K

รหัสต่อไปนี้แสดงวิธีการดำเนินการจัดกลุ่มแบบเคมีนบนชุดข้อมูลโดยใช้ค่าที่เหมาะสมที่สุดสำหรับ k ของ 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

ตารางผลลัพธ์จะแสดงการกำหนดคลัสเตอร์สำหรับการสังเกตแต่ละครั้งใน DataFrame

เพื่อให้ตีความผลลัพธ์เหล่านี้ได้ง่ายขึ้น เราสามารถเพิ่มคอลัมน์ลงใน DataFrame ที่แสดงการกำหนดคลัสเตอร์ของผู้เล่นแต่ละคน:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

คอลัมน์ คลัสเตอร์ ประกอบด้วยหมายเลขคลัสเตอร์ (0, 1 หรือ 2) ที่ผู้เล่นแต่ละคนถูกกำหนดไว้

ผู้เล่นที่อยู่ในคลัสเตอร์เดียวกันมีค่าใกล้เคียงกันโดยประมาณสำหรับ คอลัมน์คะแนน ช่วยเหลือ และ รีบาวน์

หมายเหตุ : คุณสามารถดูเอกสารฉบับเต็มเกี่ยวกับฟังก์ชัน KMeans ของ sklearn ได้ที่นี่

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีทำงานทั่วไปอื่นๆ ใน Python:

วิธีการถดถอยเชิงเส้นใน Python
วิธีการดำเนินการถดถอยโลจิสติกใน Python
วิธีดำเนินการตรวจสอบข้าม K-Fold ใน Python