การกระจายตัวอย่างคืออะไร?
ลองจินตนาการว่ามีประชากรโลมา 10,000 ตัว และน้ำหนักเฉลี่ยของโลมาในประชากรนั้นคือ 300 ปอนด์
หากเรา สุ่มตัวอย่าง โลมา 50 ตัวจากประชากรกลุ่มนี้ เราอาจพบว่าน้ำหนักเฉลี่ยของโลมาในกลุ่มตัวอย่างนี้คือ 305 ปอนด์
จากนั้น ถ้าเราสุ่มตัวอย่างง่ายๆ ของโลมา 50 ตัว เราอาจพบว่าน้ำหนักเฉลี่ยของโลมาในกลุ่มตัวอย่างนี้คือ 295 ปอนด์
เมื่อใดก็ตามที่เราสุ่มตัวอย่างโลมาง่ายๆ จำนวน 50 ตัว ก็มีแนวโน้มว่าน้ำหนักเฉลี่ยของโลมาในกลุ่มตัวอย่างจะใกล้เคียงกับจำนวนประชากรโดยเฉลี่ย 300 ปอนด์ แต่ไม่เท่ากับ 300 ปอนด์พอดี
ลองจินตนาการว่าเราสุ่มตัวอย่างง่ายๆ 200 ตัวอย่างจากปลาโลมา 50 ตัวจากประชากรกลุ่มนี้ และสร้างฮิสโตแกรมของน้ำหนักเฉลี่ยของแต่ละตัวอย่าง:
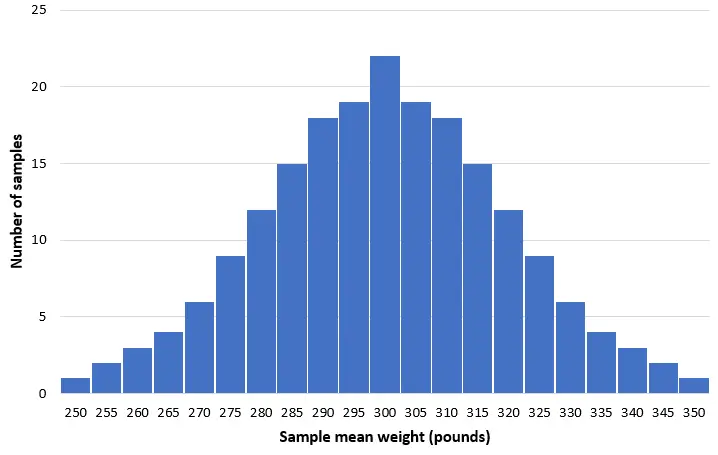
ในกลุ่มตัวอย่างส่วนใหญ่ น้ำหนักเฉลี่ยจะอยู่ที่ประมาณ 300 ปอนด์ ในบางกรณีซึ่งเกิดขึ้นไม่บ่อยนัก เราอาจเก็บตัวอย่างโลมาตัวเล็กที่มีน้ำหนักเฉลี่ยเพียง 250 ปอนด์เต็มๆ เท่านั้น หรือเราอาจจะเอาตัวอย่างโลมาปากขวดที่มีน้ำหนักเฉลี่ย 350 ปอนด์มาด้วย โดยทั่วไป การกระจาย ตัวของค่าเฉลี่ยตัวอย่างจะอยู่ที่ประมาณปกติ โดยศูนย์กลางของการกระจายอยู่ที่ศูนย์กลางที่แท้จริงของประชากร
การกระจายตัวของค่าเฉลี่ยตัวอย่างนี้เรียกว่า การกระจายตัวตัวอย่างของค่าเฉลี่ย และมีคุณสมบัติดังต่อไปนี้:
µx = µ
โดยที่ μ x คือค่าเฉลี่ยตัวอย่าง และ μ คือค่าเฉลี่ยประชากร
σx = σ/√n
โดยที่ σ x คือค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง σ คือค่าเบี่ยงเบนมาตรฐานของประชากร และ n คือขนาดของกลุ่มตัวอย่าง
ตัวอย่างเช่น ในประชากรโลมากลุ่มนี้ เรารู้ว่าน้ำหนักเฉลี่ยคือ μ = 300 ดังนั้นค่าเฉลี่ยของการกระจายตัวอย่างคือ μ x = 300
สมมติว่าเรารู้ว่าค่าเบี่ยงเบนมาตรฐานของประชากรคือ 18 ปอนด์ ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างจึงเป็น σ x = 18/ √50 = 2.546
การกระจายตัวอย่างตามสัดส่วน
พิจารณาประชากรโลมาจำนวน 10,000 ตัวเท่ากัน สมมติว่าโลมา 10% มีสีดำและที่เหลือเป็นสีเทา สมมติว่าเรา สุ่มตัวอย่าง โลมา 50 ตัวและพบว่า 14% ของโลมาในกลุ่มตัวอย่างนั้นเป็นสีดำ ต่อไป เราจะสุ่มตัวอย่างง่ายๆ ของโลมา 50 ตัว และพบว่า 8% ของโลมาในตัวอย่างนี้เป็นสีดำ
ลองนึกภาพเราสุ่มตัวอย่างโลมา 50 ตัวแบบสุ่มง่ายๆ 200 ตัวอย่างจากประชากรกลุ่มนี้ และสร้างฮิสโตแกรมของสัดส่วนโลมาสีดำในแต่ละตัวอย่าง:
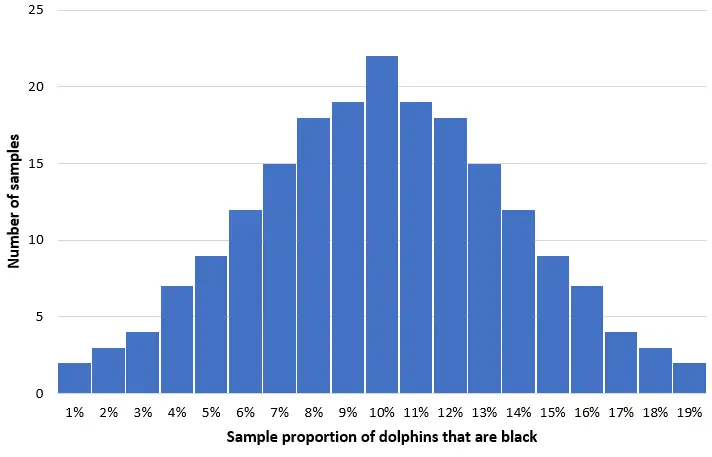
ในกลุ่มตัวอย่างส่วนใหญ่ สัดส่วนของโลมาดำจะใกล้เคียงกับจำนวนประชากรจริงที่ 10% การกระจายตัว ของสัดส่วนตัวอย่างโลมาดำจะอยู่ที่ประมาณปกติ โดยศูนย์กลางการกระจายอยู่ที่ศูนย์กลางที่แท้จริงของประชากร
การกระจายสัดส่วนตัวอย่างนี้เรียกว่า การกระจายตัวอย่างตามสัดส่วน และมีคุณสมบัติดังต่อไปนี้
µp = ป
โดยที่ p คือสัดส่วนตัวอย่างและ P คือสัดส่วนประชากร
σ p = √ (P)(1-P) / n
โดยที่ P คือสัดส่วนประชากร และ n คือขนาดของกลุ่มตัวอย่าง
ตัวอย่างเช่น ในประชากรโลมานี้ เรารู้ว่าสัดส่วนที่แท้จริงของโลมาดำคือ 10% = 0.1 ดังนั้น ค่าเฉลี่ยของการกระจายตัวอย่างตามสัดส่วนคือ μ p = 0.1
สมมติว่าเรารู้ว่าค่าเบี่ยงเบนมาตรฐานของประชากรคือ 18 ปอนด์ ดังนั้น ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างคือ σ p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042
สร้างความปกติ
หากต้องการใช้สูตรข้างต้น การกระจายตัวอย่างต้องเป็นปกติ
ตาม ทฤษฎีบทขีดจำกัดกลาง การกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่างจะอยู่ที่ประมาณปกติ หากขนาดตัวอย่างมีขนาดใหญ่เพียงพอ แม้ว่าการกระจายตัวของประชากรจะไม่ปกติก็ตาม ในกรณีส่วนใหญ่ เราจะถือว่าขนาดตัวอย่างตั้งแต่ 30 คนขึ้นไปนั้นใหญ่พอ
การกระจายตัวตัวอย่างของสัดส่วนตัวอย่างจะอยู่ที่ประมาณปกติ หากจำนวนความสำเร็จและความล้มเหลวที่คาดหวังมีค่าอย่างน้อย 10
ตัวอย่าง
เราสามารถใช้การแจกแจงตัวอย่างเพื่อคำนวณความน่าจะเป็นได้
ตัวอย่างที่ 1: เครื่องบางเครื่องสร้างคุกกี้ การกระจายน้ำหนักของคุกกี้เหล่านี้จะเอียงไปทางขวาโดยมีค่าเฉลี่ย 10 ออนซ์ และส่วนเบี่ยงเบนมาตรฐาน 2 ออนซ์ หากเราสุ่มตัวอย่างคุกกี้ง่ายๆ จำนวน 100 ชิ้นที่ผลิตโดยเครื่องนี้ ความน่าจะเป็นที่น้ำหนักเฉลี่ยของคุกกี้ในตัวอย่างนี้น้อยกว่า 9.8 ออนซ์ เป็นเท่าใด
ขั้นตอนที่ 1: สร้างสภาวะปกติ
เราจำเป็นต้องตรวจสอบให้แน่ใจว่าการกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่างเป็นไปตามปกติ เนื่องจากขนาดตัวอย่างของเรามากกว่าหรือเท่ากับ 30 ตามทฤษฎีบทขีดจำกัดกลาง เราจึงสามารถสรุปได้ว่าการกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่างเป็นเรื่องปกติ
ขั้นตอนที่ 2: ค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการกระจายตัวอย่าง
µx = µ
σx = σ/√n
ไมโคร x = 10 ออนซ์
σ x = 2/ √100 = 2/10 = 0.2 ออนซ์
ขั้นตอนที่ 3: ใช้ เครื่องคำนวณพื้นที่คะแนน Z เพื่อกำหนดความน่าจะเป็นที่น้ำหนักคุกกี้เฉลี่ยในตัวอย่างนี้จะน้อยกว่า 9.8 ออนซ์
ป้อนตัวเลขต่อไปนี้ลงใน เครื่องคำนวณพื้นที่คะแนน Z คุณสามารถเว้นว่าง “คะแนนดิบ 2” ไว้ได้ เนื่องจากในตัวอย่างนี้เราจะพบตัวเลขเพียงตัวเดียวเท่านั้น
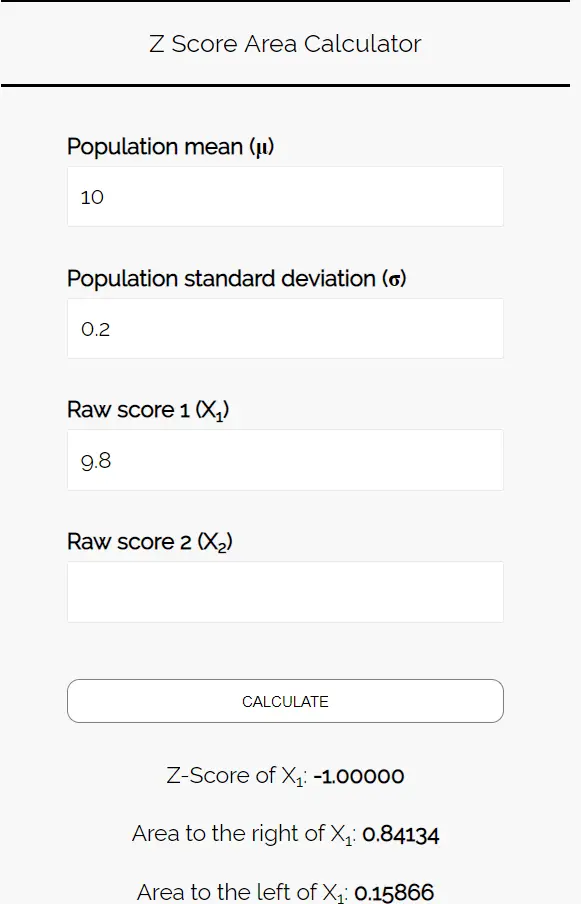
เนื่องจากเราต้องการทราบความน่าจะเป็นที่น้ำหนักเฉลี่ยของคุกกี้ในกลุ่มตัวอย่างนี้ น้อยกว่า 9.8 ออนซ์ เราจึงสนใจพื้นที่ทาง ด้านซ้าย ของ 9.8 เครื่องคิดเลขบอกเราว่าความน่าจะเป็นนี้คือ 0.15866
ตัวอย่างที่ 2: จากการศึกษาทั่วทั้งโรงเรียน 87% ของนักเรียนในโรงเรียนแห่งใดแห่งหนึ่งชอบพิซซ่ามากกว่าไอศกรีม สมมติว่าเราสุ่มตัวอย่างง่ายๆ จำนวน 200 คน ความน่าจะเป็นที่สัดส่วนของนักเรียนที่ชอบทานพิซซ่าน้อยกว่า 85% เป็นเท่าใด
ขั้นตอนที่ 1: สร้างสภาวะปกติ
โปรดทราบว่าการกระจายตัวตัวอย่างของสัดส่วนตัวอย่างจะอยู่ที่ประมาณปกติ หากจำนวน “ความสำเร็จ” และ “ความล้มเหลว” ที่คาดหวังมีค่าอย่างน้อย 10 ทั้งคู่
ในกรณีนี้ จำนวนนักเรียนที่จะชอบพิซซ่าที่คาดหวังคือ 87% * นักเรียน 200 คน = นักเรียน 174 คน จำนวนนักเรียนที่คาดว่าจะไม่ชอบพิซซ่าคือ 13% * นักเรียน 200 คน = นักเรียน 26 คน เนื่องจากตัวเลขทั้งสองมีค่าอย่างน้อย 10 เราจึงสามารถสรุปได้ว่าการกระจายตัวอย่างตามสัดส่วนของนักเรียนที่ชอบพิซซ่านั้นค่อนข้างจะปกติ
ขั้นตอนที่ 2: ค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการกระจายตัวอย่าง
µp = ป
σ p = √ (P)(1-P) / n
ไมโครพี = 0.87
σ พี = √ (0.87)(1-0.87) / 200 = 0.024
ขั้นตอนที่ 3: ใช้ เครื่องคำนวณพื้นที่คะแนน Z เพื่อกำหนดความน่าจะเป็นที่สัดส่วนของนักเรียนที่เลือกพิซซ่าน้อยกว่า 85%
ป้อนตัวเลขต่อไปนี้ลงใน เครื่องคำนวณพื้นที่คะแนน Z คุณสามารถเว้นว่าง “คะแนนดิบ 2” ไว้ได้ เนื่องจากในตัวอย่างนี้เราจะพบตัวเลขเพียงตัวเดียวเท่านั้น
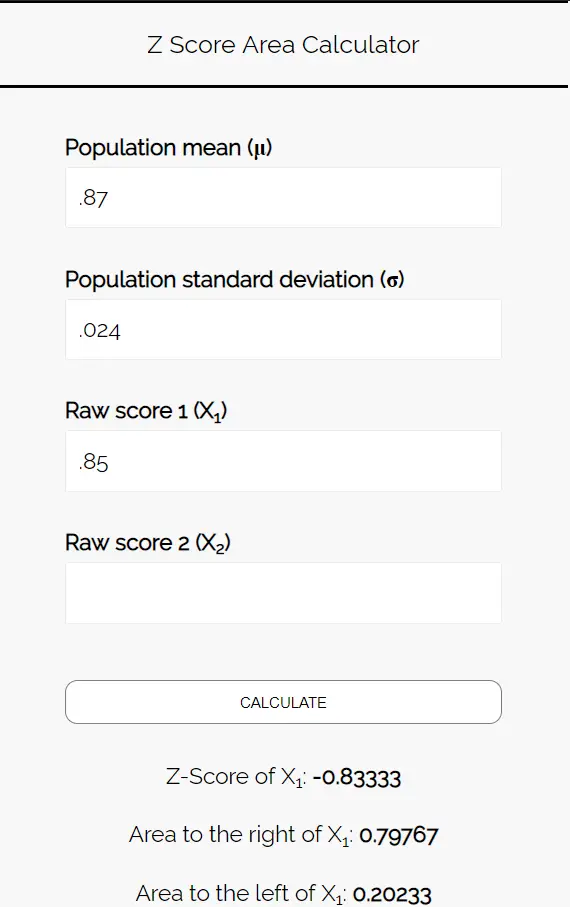
เนื่องจากเราต้องการทราบความน่าจะเป็นที่สัดส่วนของนักเรียนที่ชอบทานพิซซ่าน้อยกว่า 85% เราจึงสนใจพื้นที่ทาง ด้านซ้าย ของ 0.85 เครื่องคิดเลขบอกเราว่าความน่าจะเป็นนี้คือ 0.20233