วิธีแยกสารตกค้างจากฟังก์ชัน lm() ใน r

คุณสามารถใช้ไวยากรณ์ต่อไปนี้เพื่อแยก ส่วนที่เหลือ จากฟังก์ชัน lm() ใน R:

 fit$residuals

ตัวอย่างนี้ถือว่าเราใช้ฟังก์ชัน lm() เพื่อให้พอดีกับโมเดลการถดถอยเชิงเส้นและตั้งชื่อผลลัพธ์ ให้ พอดี

ตัวอย่างต่อไปนี้แสดงวิธีใช้ไวยากรณ์นี้ในทางปฏิบัติ

ที่เกี่ยวข้อง: วิธีแยก R-Squared ออกจากฟังก์ชัน lm() ใน R

ตัวอย่าง: วิธีแยกสารตกค้างจาก lm() ใน R

สมมติว่าเรามีกรอบข้อมูลต่อไปนี้ใน R ซึ่งมีข้อมูลเกี่ยวกับนาทีที่เล่น การฟาวล์ทั้งหมด และคะแนนรวมที่ผู้เล่นบาสเก็ตบอล 10 คนทำได้:

 #create data frame
df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40),
                 fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1),
                 points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30))

#view data frame
df

   minutes fouls points
1 5 5 6
2 10 5 8
3 13 3 8
4 14 4 7
5 20 2 14
6 22 1 10
7 26 3 22
8 34 2 24
9 38 1 28
10 40 1 30

สมมติว่าเราต้องการปรับโมเดลการถดถอยเชิงเส้นพหุคูณต่อไปนี้:

คะแนน = β ₀ + β ₁ (นาที) + β ₂ (ฟาวล์)

เราสามารถใช้ฟังก์ชัน lm() เพื่อให้เหมาะกับโมเดลการถดถอยนี้:

 #fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)

จากนั้นเราสามารถพิมพ์ fit$residuals เพื่อแยกส่วนที่เหลือออกจากแบบจำลอง:

 #extract residuals from model
fit$residuals

         1 2 3 4 5 6 7 
 2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786 
         8 9 10 
-1.7048752 0.5692404 0.6144057

เนื่องจากมีการสังเกตทั้งหมด 10 รายการในฐานข้อมูลของเรา จึงเหลือ 10 รายการที่เหลือ – หนึ่งรายการสำหรับการสังเกตแต่ละครั้ง

ตัวอย่างเช่น:

• การสังเกตครั้งแรกมีสารตกค้าง 2,089 .
• การสังเกตครั้งที่สองมีค่าตกค้าง -0.798
• การสังเกตครั้งที่สามมีค่าตกค้าง 0.637

และอื่นๆ

จากนั้นเราสามารถสร้างพล็อตของส่วนที่เหลือเทียบกับค่าที่ติดตั้งได้หากเราต้องการ:

 #store residuals in variable
res <- fit$residuals

#produce residual vs. fitted plot
plot(fitted(fit), res)

#add a horizontal line at 0 
abline(0,0)

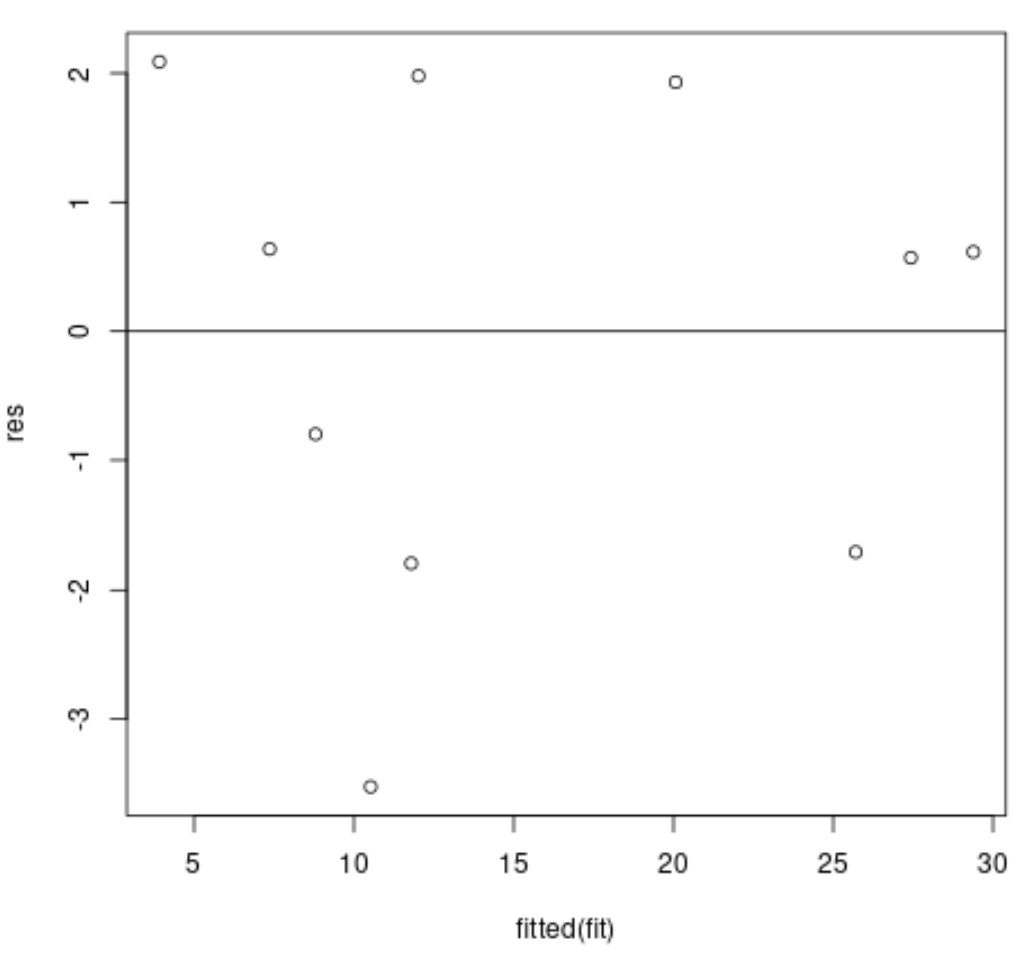
แกน x จะแสดงค่าที่พอดี และแกน y จะแสดงค่าคงเหลือ

ตามหลักการแล้ว สารตกค้างควรสุ่มกระจัดกระจายรอบๆ ศูนย์ โดยไม่มีรูปแบบที่ชัดเจน เพื่อให้แน่ใจว่าเป็นไปตาม สมมติฐานการรักร่วมเพศ

ในแผนภาพสารตกค้างด้านบน เราจะเห็นว่าสารตกค้างดูเหมือนจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์โดยไม่มีรูปแบบที่ชัดเจน ซึ่งหมายความว่ามีแนวโน้มที่จะเป็นไปตามสมมติฐานของความเป็นเนื้อเดียวกัน

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีสร้างพล็อตที่เหลือใน R