สัมประสิทธิ์สหสัมพันธ์เพียร์สัน

ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน (หรือเรียกอีกอย่างว่า “ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างผลิตภัณฑ์-ช่วงเวลา”) คือการวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปร X และ Y สองตัว โดยมีค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

สูตรการหาสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน

สูตรในการค้นหาสัมประสิทธิ์สหสัมพันธ์เพียร์สัน แทนด้วย r สำหรับตัวอย่างข้อมูลคือ ( ผ่าน Wikipedia ):

คุณอาจไม่ต้องคำนวณสูตรนี้ด้วยตนเองเลยเพราะคุณสามารถใช้ซอฟต์แวร์คำนวณแทนได้ แต่การทำความเข้าใจว่าสูตรนี้ทำอะไรได้บ้างโดยดูตัวอย่างต่างๆ

สมมติว่าเรามีชุดข้อมูลต่อไปนี้:

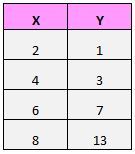
หากเราพล็อตคู่เหล่านี้ (X, Y) บนแผนภาพกระจาย มันจะมีลักษณะดังนี้:

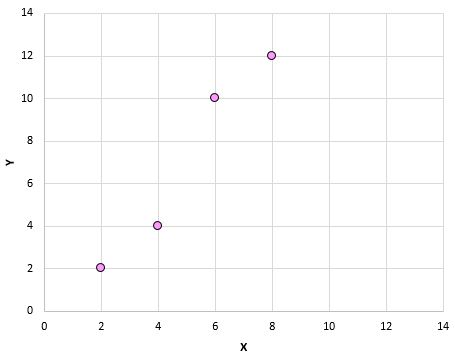
เพียงดูแผนภาพกระจายนี้ เราจะเห็นว่ามีความสัมพันธ์เชิงบวกระหว่างตัวแปร X และ Y: เมื่อ X เพิ่มขึ้น Y ก็มีแนวโน้มที่จะเพิ่มขึ้นเช่นกัน แต่เพื่อที่จะหาจำนวนที่แน่นอนของความสัมพันธ์เชิงบวกของตัวแปรทั้งสองนี้ เราจำเป็นต้องค้นหาสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน

เรามาเน้นที่ตัวเศษของสูตรกัน:

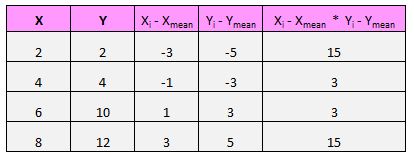
สำหรับแต่ละคู่ (X, Y) ในชุดข้อมูลของเรา เราจำเป็นต้องค้นหาความแตกต่างระหว่างค่า x และค่า x เฉลี่ย ความแตกต่างระหว่างค่า y และค่า y เฉลี่ย แล้วคูณตัวเลขทั้งสองนี้เข้าด้วยกัน

ตัวอย่างเช่น คู่แรกของเรา (X, Y) คือ (2, 2) ค่าเฉลี่ยของ x ในชุดข้อมูลนี้คือ 5 และค่าเฉลี่ยของ y ในชุดข้อมูลนี้คือ 7 ดังนั้นความแตกต่างระหว่างค่า x ของคู่นี้กับค่าเฉลี่ยของ x คือ 2 – 5 = -3 ความแตกต่างระหว่างค่า y ของคู่นี้กับค่า y เฉลี่ยคือ 2 – 7 = -5 จากนั้นเมื่อเราคูณตัวเลขสองตัวนี้ เราจะได้ -3 * -5 = 15

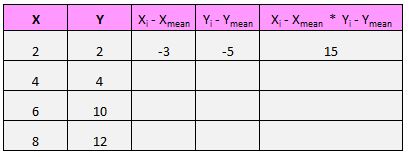
นี่คือภาพรวมของสิ่งที่เราเพิ่งทำ:

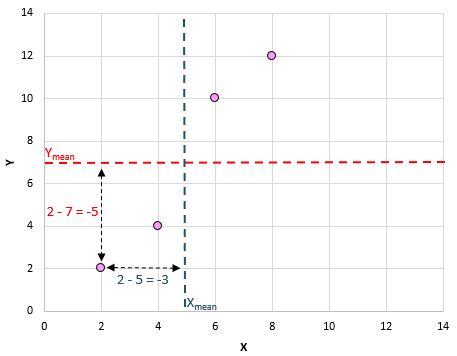
จากนั้นทำสิ่งนี้กับแต่ละคู่:

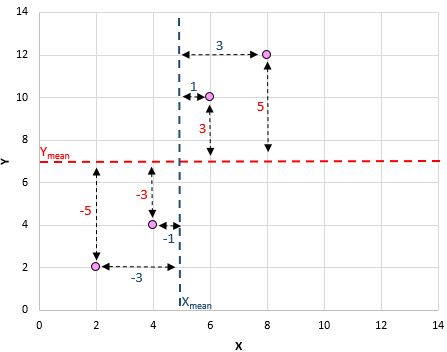
ขั้นตอนสุดท้ายในการรับตัวเศษของสูตรคือการบวกค่าเหล่านี้ทั้งหมดเข้าด้วยกัน:

15 + 3 +3 + 15 = 36

จากนั้นตัวส่วนของสูตรบอกให้เราหาผลรวมของผลต่างกำลังสองทั้งหมดของ x และ y จากนั้นนำตัวเลขทั้งสองนี้มาคูณกัน จากนั้นหารากที่สอง:

ก่อนอื่น เราจะหาผลรวมของกำลังสองของส่วนต่างของ x และ y:

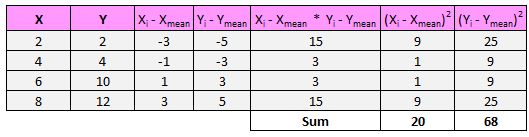
ต่อไป เราจะคูณตัวเลขสองตัวนี้ด้วยกัน: 20 * 68 = 1,360

สุดท้าย เราจะหารากที่สอง: √ 1,360 = 36.88

เราจึงพบว่าตัวเศษของสูตรคือ 36 และตัวส่วนคือ 36.88 ซึ่งหมายความว่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันของเราคือ r = 36 / 36.88 = 0.976

จำนวนนี้ใกล้กับ 1 ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงเส้นเชิงบวกที่ชัดเจนระหว่างตัวแปร X และ Y ซึ่งเป็นการยืนยันความสัมพันธ์ที่เราสังเกตเห็นในแผนภาพกระจาย

ดูความสัมพันธ์

โปรดจำไว้ว่าค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันบอกเราถึง ประเภท ของความสัมพันธ์เชิงเส้น (บวก ลบ ไม่มี) ระหว่างตัวแปรสองตัว รวมถึง จุดแข็ง ของความสัมพันธ์นี้ (อ่อน ปานกลาง และรุนแรง)

เมื่อเราสร้างแผนภาพกระจายของตัวแปรสองตัว เราจะ เห็น ความสัมพันธ์ที่แท้จริงระหว่างตัวแปรสองตัว ต่อไปนี้เป็นความสัมพันธ์เชิงเส้นหลายประเภทที่เราอาจสังเกตเห็น:

ความสัมพันธ์เชิงบวกที่แข็งแกร่ง: เมื่อตัวแปรบนแกน x เพิ่มขึ้น ตัวแปรบนแกน y ก็จะเพิ่มขึ้นเช่นกัน ประเด็นต่างๆ กระจุกตัวกันอย่างใกล้ชิด บ่งบอกถึงความสัมพันธ์อันแน่นแฟ้น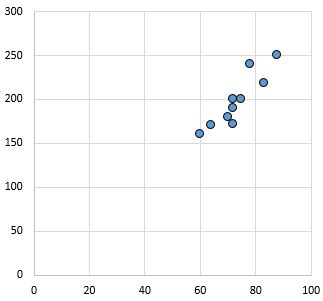

ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน: 0.94

ความสัมพันธ์ที่อ่อนแอและเป็นเชิงบวก: เมื่อตัวแปรบนแกน x เพิ่มขึ้น ตัวแปรบนแกน y ก็จะเพิ่มขึ้นเช่นกัน แต้มค่อนข้างกระจัดกระจายบ่งบอกถึงความสัมพันธ์ที่อ่อนแอ

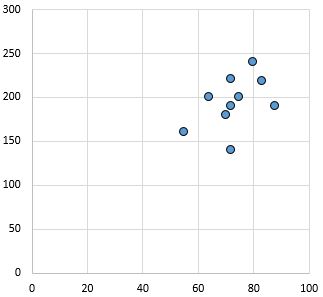
ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน: 0.44

ไม่มีความสัมพันธ์: ไม่มีความสัมพันธ์ที่ชัดเจน (บวกหรือลบ) ระหว่างตัวแปร

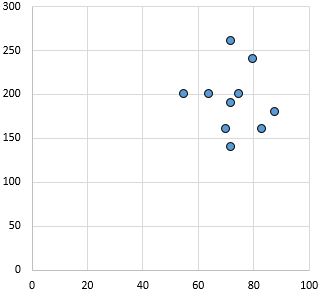
ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน: 0.03

ความสัมพันธ์เชิงลบที่แข็งแกร่ง: เมื่อตัวแปรบนแกน x เพิ่มขึ้น ตัวแปรบนแกน y จะลดลง ประเด็นอัดแน่นบ่งบอกถึงความสัมพันธ์อันแน่นแฟ้น

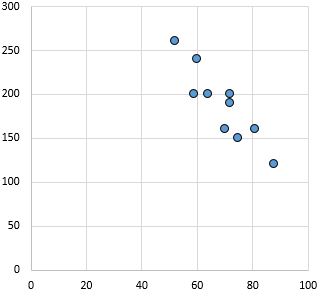
ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน: -0.87

ความสัมพันธ์ที่อ่อนแอและเป็นลบ: เมื่อตัวแปรบนแกน x เพิ่มขึ้น ตัวแปรบนแกน y จะลดลง แต้มค่อนข้างกระจัดกระจายบ่งบอกถึงความสัมพันธ์ที่อ่อนแอ

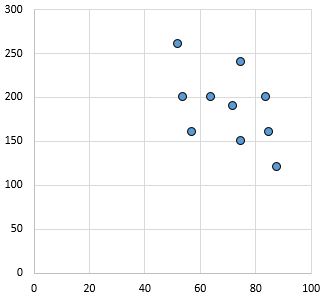
ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน: – 0.46

การทดสอบความสำคัญของสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน

เมื่อเราค้นหาค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันสำหรับชุดข้อมูล เรามักจะทำงานกับ ตัวอย่าง ข้อมูลจาก ประชากรกลุ่ม ใหญ่ ซึ่งหมายความว่า มีความเป็นไปได้ที่จะค้นหาความสัมพันธ์ที่ไม่เป็นศูนย์สำหรับตัวแปรสองตัว แม้ว่าตัวแปรทั้งสองจะไม่มีความสัมพันธ์กันในประชากรโดยรวมก็ตาม

ตัวอย่างเช่น สมมติว่าเราสร้างแผนภาพกระจายสำหรับตัวแปร X และ Y สำหรับแต่ละจุดข้อมูลในประชากรทั้งหมด และมีลักษณะดังนี้:

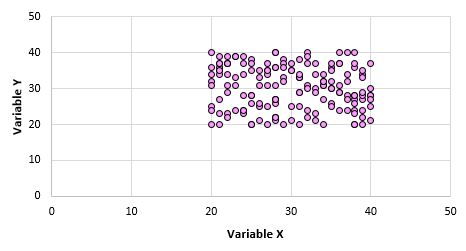
เห็นได้ชัดว่าตัวแปรทั้งสองนี้ไม่มีความสัมพันธ์กัน อย่างไรก็ตาม เป็นไปได้ว่าเมื่อเราสุ่มตัวอย่างจำนวน 10 คะแนนจากประชากร เราจะเลือกจุดต่อไปนี้

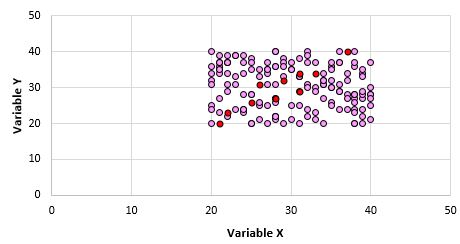
เราจะเห็นว่าค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันสำหรับตัวอย่างคะแนนนี้คือ 0.93 ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงบวกอย่างมาก แม้ว่าความสัมพันธ์ของประชากรจะเป็นศูนย์ก็ตาม

เพื่อทดสอบว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองมีนัยสำคัญทางสถิติหรือไม่ เราสามารถค้นหาสถิติการทดสอบต่อไปนี้:

สถิติการทดสอบ T = r * √ (n-2) / (1-r ² )

โดยที่ n คือจำนวนคู่ในกลุ่มตัวอย่างของเรา r คือสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน และสถิติการทดสอบ T เป็นไปตามการแจกแจงด้วยดีกรีอิสระ n-2

เรามาทบทวนตัวอย่างวิธีทดสอบความสำคัญของสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน

ตัวอย่าง

ชุดข้อมูลต่อไปนี้แสดงส่วนสูงและน้ำหนักของบุคคล 12 คน:

แผนภาพกระจายด้านล่างแสดงค่าของตัวแปรทั้งสองนี้:

ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันสำหรับตัวแปรทั้งสองนี้คือ r = 0.836

สถิติการทดสอบ T = 0.836 * √ (12 -2) / (1-0.836 ² ) = 4.804

จาก เครื่องคำนวณการแจกแจงแบบ t คะแนน 4.804 โดยมีดีกรีอิสระ 10 องศามีค่า p เท่ากับ 0.0007 ตั้งแต่ 0.0007 < 0.05 เราสามารถสรุปได้ว่าความสัมพันธ์ระหว่างน้ำหนักและส่วนสูงในตัวอย่างนี้มีนัยสำคัญทางสถิติที่ alpha = 0.05

ข้อควรระวัง

แม้ว่าค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันจะมีประโยชน์ในการบอกเราว่าตัวแปรสองตัวมีการเชื่อมโยงเชิงเส้นหรือไม่ เราต้องคำนึงถึงสามสิ่งเมื่อตีความค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน:

1. ความสัมพันธ์ไม่ได้หมายความถึงสาเหตุ ไม่ใช่เพราะว่าตัวแปรสองตัวมีความสัมพันธ์กันที่ ทำให้ ตัวแปรหนึ่งปรากฏบ่อยขึ้นหรือน้อยลง ตัวอย่างคลาสสิกของเรื่องนี้คือความสัมพันธ์เชิงบวกระหว่างการขายไอศกรีมและการโจมตีของฉลาม เมื่อยอดขายไอศกรีมเพิ่มขึ้นในบางช่วงเวลาของปี การโจมตีของฉลามก็มีแนวโน้มเพิ่มขึ้นเช่นกัน

นี่หมายความว่าการกินไอศกรีม ทำให้เกิด การโจมตีของฉลามใช่หรือไม่? ไม่แน่นอน! ซึ่งหมายความว่าในช่วงฤดูร้อน การบริโภคน้ำแข็งและการโจมตีของฉลามมีแนวโน้มที่จะเพิ่มขึ้น เนื่องจากน้ำแข็งเป็นที่นิยมมากขึ้นในช่วงฤดูร้อน และผู้คนจำนวนมากลงสู่มหาสมุทรในช่วงฤดูร้อน

2. ความสัมพันธ์มีความอ่อนไหวต่อค่าผิดปกติ ค่าผิดปกติที่รุนแรงสามารถเปลี่ยนค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันได้อย่างมาก ลองพิจารณาตัวอย่างด้านล่าง:

ตัวแปร X และ Y มีค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันเท่ากับ 0.00 แต่ลองจินตนาการว่าเรามีค่าผิดปกติในชุดข้อมูล:

อย่างไรก็ตาม ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันสำหรับตัวแปรทั้งสองนี้คือ 0.878 สิ่งนี้เปลี่ยนแปลงทุกสิ่ง ด้วยเหตุนี้ เมื่อคำนวณความสัมพันธ์ของตัวแปรสองตัว จึงควรแสดงภาพตัวแปรโดยใช้ Scatterplot เพื่อตรวจสอบค่าผิดปกติ

3. ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันไม่ได้จับความสัมพันธ์แบบไม่เชิงเส้นระหว่างตัวแปรสองตัว สมมติว่าเรามีตัวแปรสองตัวที่มีความสัมพันธ์ดังต่อไปนี้:

ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันสำหรับตัวแปรทั้งสองนี้คือ 0.00 เนื่องจากไม่มีความสัมพันธ์เชิงเส้น อย่างไรก็ตาม ตัวแปรทั้งสองนี้มีความสัมพันธ์แบบไม่เชิงเส้น ค่า y เป็นเพียงค่า x กำลังสอง

เมื่อใช้สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน โปรดจำไว้ว่าคุณกำลังทดสอบว่าตัวแปรสองตัวมีความสัมพันธ์ เชิงเส้นตรง หรือไม่ แม้ว่าค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันจะบอกเราว่าตัวแปรสองตัวนั้นไม่มีความสัมพันธ์กัน ตัวแปรเหล่านั้นก็ยังสามารถมีความสัมพันธ์แบบไม่เชิงเส้นบางประเภทได้ นี่เป็นอีกเหตุผลหนึ่งว่าทำไมการสร้างแผนภาพกระจายเมื่อวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรสองตัวจึงมีประโยชน์ กล่าวคือ ช่วยให้คุณตรวจพบความสัมพันธ์แบบไม่เชิงเส้นได้