การสุ่มตัวอย่างแบบแบ่งชั้น

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 6, 2023 สถิติ 0 ความคิดเห็น

ในบทความนี้ เราจะอธิบายว่าการสุ่มตัวอย่างแบบแบ่งชั้นคืออะไร และดำเนินการอย่างไร คุณจะพบคำอธิบายเกี่ยวกับประเภทย่อยของการสุ่มตัวอย่างแบบแบ่งชั้น และสุดท้ายคือข้อดีและข้อเสียของการสุ่มตัวอย่างแบบแบ่งชั้น

การสุ่มตัวอย่างแบบแบ่งชั้นคืออะไร?

การสุ่มตัวอย่างแบบแบ่งชั้น เป็นวิธีการทางสถิติที่ใช้ในการเลือกองค์ประกอบของตัวอย่างโดยการแบ่งประชากรออกเป็นกลุ่ม (เรียกว่าชั้น) กล่าวคือ ในการสุ่มตัวอย่างแบบแบ่งชั้น ประชากรจะถูกแบ่งออกเป็นชั้น และบุคคลจากแต่ละชั้นจะถูกสุ่มเลือกเพื่อสร้างกลุ่มตัวอย่างในการศึกษาทั้งหมด

ชั้นคือกลุ่มที่เป็นเนื้อเดียวกัน หรืออีกนัยหนึ่ง บุคคลในชั้นหนึ่งมีลักษณะเฉพาะของตนเองที่ทำให้พวกเขาแตกต่างจากชั้นอื่น บุคคลจึงสามารถอยู่ในชั้นเดียวเท่านั้น

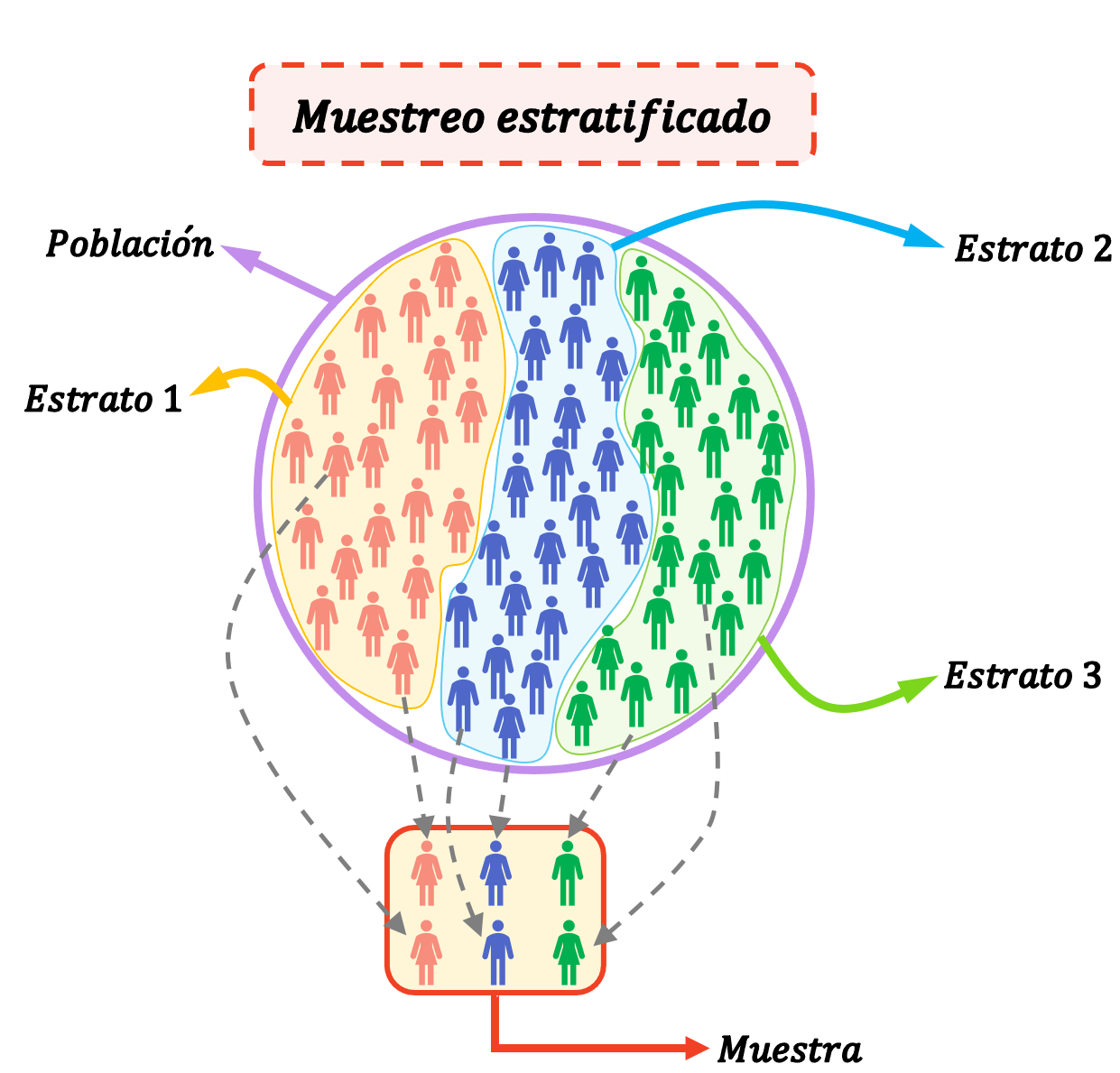
การสุ่มตัวอย่างแบบแบ่งชั้นมีประโยชน์มากเมื่อประชากรประกอบด้วยกลุ่มที่เป็นเนื้อเดียวกันและมีความแตกต่างกันมาก

ตามหลักเหตุผลแล้ว ผลรวมของขนาดของชั้นทั้งหมดจะให้ขนาดของประชากรทางสถิติ:

$N=N_1+N_2+N_3+\dots+N_k$

ในทำนองเดียวกัน ผลรวมของขนาดตัวอย่างที่เลือกในแต่ละชั้นจะเท่ากับขนาดตัวอย่างรวมของการศึกษาทางสถิติ:

$n=n_1+n_2+n_3+\dots+n_k$

โดยทั่วไปเราจะแยกความแตกต่างระหว่างอักษรตัวพิมพ์ใหญ่และตัวพิมพ์เล็กเพื่อระบุประชากรหรือกลุ่มตัวอย่างตามลำดับ

วิธีการสุ่มตัวอย่างแบบแบ่งชั้น

ขั้นตอนในการสุ่มตัวอย่างแบบแบ่งชั้นมีดังนี้:

กำหนดประชากรเป้าหมาย
เลือก การแบ่งชั้นของตัวแปร และจำนวนชั้นที่จะมี
ระบุว่า แต่ละองค์ประกอบของประชากรอยู่ในชั้นใด
คำนวณ ขนาดของแต่ละชั้น ที่จะเป็นส่วนหนึ่งของตัวอย่าง
สุ่มเลือกองค์ประกอบจากแต่ละชั้น ที่จะอยู่ในตัวอย่างการศึกษา สำหรับแต่ละชั้น จะต้องเลือกองค์ประกอบให้มากที่สุดเท่าที่จะตัดสินใจในขั้นตอนก่อนหน้า

โปรดทราบว่าขนาดแต่ละชั้นจะแสดงในตัวอย่างไม่เพียงแต่ขึ้นอยู่กับขนาดของชั้นชั้นนั้นเท่านั้น แต่ยังขึ้นอยู่กับประเภทของการสุ่มตัวอย่างแบบแบ่งชั้นด้วย จากนั้น จะมีการอธิบายการสุ่มตัวอย่างแบบแบ่งชั้นแต่ละประเภท และวิธีการคำนวณขนาดตัวอย่างของแต่ละชั้นโดยใช้ตัวอย่าง

ประเภทของการสุ่มตัวอย่างแบบแบ่งชั้น

เมื่อคุณทราบคำจำกัดความของการสุ่มตัวอย่างแบบแบ่งชั้นแล้ว คุณควรทราบว่าการสุ่มตัวอย่างแบบแบ่งชั้นมีหลายประเภท ซึ่งจำแนกได้ดังนี้

การสุ่มตัวอย่างแบบแบ่งชั้นตามสัดส่วน
การสุ่มตัวอย่างแบบแบ่งชั้นสม่ำเสมอ
การสุ่มตัวอย่างมี ความเหมาะสมที่สุด

การสุ่มตัวอย่างแบบแบ่งชั้นแต่ละประเภทจะมีการอธิบายโดยละเอียดด้านล่างเพื่อให้เข้าใจความหมายของแต่ละประเภทได้ดียิ่งขึ้น

การสุ่มตัวอย่างแบบแบ่งชั้นตามสัดส่วน

ใน การสุ่มตัวอย่างแบบแบ่งชั้นตามสัดส่วน หรือการสุ่มตัวอย่างแบบจัดสรรตามสัดส่วน จำนวนองค์ประกอบจากแต่ละชั้นที่เป็นส่วนหนึ่งของตัวอย่างในการศึกษาจะเป็นสัดส่วนกับขนาดของแต่ละชั้น

ดังนั้น หากชั้นหนึ่งมีขนาดใหญ่กว่าอีกชั้นหนึ่ง ตัวอย่างสุดท้ายก็จะมีองค์ประกอบเพิ่มเติมจากชั้นนั้น ในทางกลับกัน หากชั้นหนึ่งมีขนาดเล็กกว่าอีกชั้นหนึ่ง ก็จะมีองค์ประกอบน้อยลงจากชั้นนี้ในตัวอย่างการวิเคราะห์ทางสถิติ

การสุ่มตัวอย่างแบบแบ่งชั้นประเภทนี้มีประโยชน์เมื่อชั้นมีขนาดต่างกัน และเราต้องการให้ตัวอย่างรวมองค์ประกอบเพิ่มเติมจากชั้นที่ใหญ่กว่า

ใน การคำนวณจำนวนองค์ประกอบจากแต่ละชั้น ที่จะอยู่ในตัวอย่าง ขนาดของแต่ละชั้นจะต้องหารด้วยผลรวมของขนาดของชั้นทั้งหมด ผลลัพธ์ที่ได้จะเป็นสัดส่วนของชั้นที่ควรรวมไว้ในตัวอย่าง ดังนั้นจะต้องคูณด้วยขนาดตัวอย่างที่ต้องการ

$n_i=n\cdot \cfrac{N_i}{N_1+N_2+\dots +N_k}=n\cdot \cfrac{N_i}{N}$

ทอง

$n$

คือขนาดตัวอย่างทั้งหมดที่ต้องการ

$n_i$

จำนวนองค์ประกอบในชั้น

$i$

ที่จะรวมไว้ในตัวอย่าง

$N_i$

ขนาดชั้น

$i$

, และ

$N$

จำนวนองค์ประกอบทั้งหมดในประชากร

ตัวอย่างเช่น ลองจินตนาการว่าเราต้องการศึกษาในบริษัทที่มีพนักงาน 150 คน โดยสุ่มตัวอย่าง 50 คน และแบ่งชั้นข้อมูลตามอายุของพนักงาน เราสามารถจำแนกข้อมูลได้ดังนี้

อายุ 20 ถึง 29 ปี: 35 คน
อายุ 30 ถึง 39 ปี: พนักงาน 57 คน
อายุ 40 ถึง 49 ปี: พนักงาน 42 คน
อายุ 50 ถึง 59 ปี: พนักงาน 16 คน

ดังนั้น หากเราแบ่งชั้นข้อมูลตามสัดส่วน การสุ่มตัวอย่างจะเป็นดังนี้:

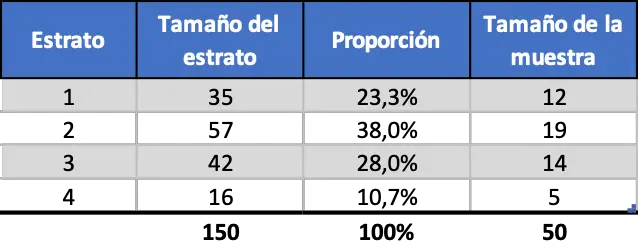
การสุ่มตัวอย่างแบบแบ่งชั้นสม่ำเสมอ

ใน การสุ่มตัวอย่างแบบแบ่งชั้นสม่ำเสมอ หรือการสุ่มตัวอย่างแบบแบ่งชั้นสม่ำเสมอ จำนวนองค์ประกอบจากแต่ละชั้นที่เป็นส่วนหนึ่งของตัวอย่างการศึกษาจะเท่ากัน

แต่ละชั้นจึงมีน้ำหนักเท่ากันในการสุ่มตัวอย่างประเภทนี้ ไม่ว่าชั้นหนึ่งจะมีจำนวนบุคคลมากหรือน้อยกว่าชั้นอื่น ทั้งหมดจะถูกแสดงในกลุ่มตัวอย่างด้วยจำนวนบุคคลเท่ากัน

ในกรณีนี้ ใน การคำนวณขนาดขององค์ประกอบในแต่ละชั้น ต้องหารขนาดตัวอย่างที่ต้องการด้วยจำนวนชั้นที่มีอยู่ กล่าวอีกนัยหนึ่ง ควรใช้สูตรต่อไปนี้:

$n_i=\cfrac{n}{k}$

ทอง

$n$

คือขนาดตัวอย่างทั้งหมดที่ต้องการ

$n_i$

จำนวนองค์ประกอบในชั้น

$i$

ใครจะรวมอยู่ในกลุ่มตัวอย่างและ

$k$

จำนวนชั้นที่ประชากรถูกแบ่งออก

ตามตัวอย่างก่อนหน้านี้ เนื่องจากเราต้องการตัวอย่างที่มีคนงาน 50 คน และทั้งหมดมีชั้นที่แตกต่างกัน 4 ชั้น ขนาดตัวอย่างของแต่ละชั้นจะเป็น:

$n_i=\cfrac{50}{4}=12,5$

ผลลัพธ์เป็นเลขฐานสิบ บางชั้นจะมีคนงาน 12 คน และอีก 13 คนจนกว่าจะถึง 50 คน ดังนั้นการสุ่มตัวอย่างแบบแบ่งชั้นสม่ำเสมอจึงเป็นดังนี้:

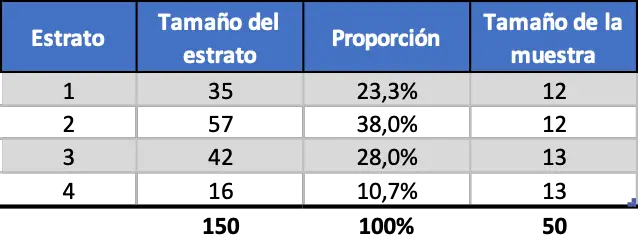
อย่างที่คุณเห็น ขนาดตัวอย่างของแต่ละชั้นไม่ขึ้นอยู่กับสัดส่วนของแต่ละชั้น

การสุ่มตัวอย่างแบบแบ่งชั้นที่เหมาะสมที่สุด

ใน การสุ่มตัวอย่างแบบแบ่งชั้นที่เหมาะสมที่สุด จำนวนองค์ประกอบในแต่ละชั้นจะขึ้นอยู่กับความแปรปรวนของแต่ละชั้นตามสัดส่วน

ดังนั้น ชั้นที่มีความแปรปรวนน้อยกว่าจะมีขนาดตัวอย่างที่ใหญ่กว่า และในทางกลับกัน ชั้นที่มีความแปรปรวนน้อยกว่าจะมีขนาดตัวอย่างที่เล็กกว่า

สูตรกำหนดจำนวนองค์ประกอบจากแต่ละชั้นที่จะเป็นส่วนหนึ่งของตัวอย่างการศึกษาทางสถิติมีดังนี้

$n_i=n\cdot \cfrac{\sigma_i\cdot N_i}{\displaystyle \sum_{j=1}^k \sigma_j\cdot N_j }$

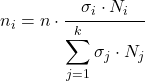
ทอง

$n$

คือขนาดตัวอย่างทั้งหมดที่ต้องการ

$n_i$

คือจำนวนองค์ประกอบในชั้น

$i$

ที่จะรวมไว้ในตัวอย่าง

$\sigma_i$

คือค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนทั่วไป) ของชั้นสตราตัม

$i$

, และ

$N_i$

คือขนาดของชั้นชั้น

$i$

ข้อดีและข้อเสียของการสุ่มตัวอย่างแบบแบ่งชั้น

การสุ่มตัวอย่างแบบแบ่งชั้นมีข้อดีและข้อเสียดังต่อไปนี้:

ข้อได้เปรียบ	ข้อเสีย
ทำให้สามารถศึกษาทางสถิติได้ไม่เพียงแต่ประชากรทั้งหมดเท่านั้น แต่ยังรวมถึงแต่ละชั้นโดยเฉพาะด้วย	นี่เป็นวิธีการสุ่มตัวอย่างที่ซับซ้อนในการดำเนินการ
ข้อผิดพลาดในการสุ่มตัวอย่างที่เกิดขึ้นจากการสุ่มตัวอย่างแบบแบ่งชั้นจะเท่ากับหรือน้อยกว่าข้อผิดพลาดของการสุ่มตัวอย่างแบบธรรมดาเสมอ	กระบวนการสุ่มตัวอย่างนี้ใช้เวลานานและมีราคาแพง
ช่วยให้คุณสามารถใช้ประโยชน์จากความรู้ของนักวิจัยเกี่ยวกับประชากรได้	ตัวอย่างที่วิเคราะห์จำเป็นต้องมีข้อมูลจำนวนมากเพื่อให้สามารถแบ่งชั้นได้
ด้วยการสุ่มตัวอย่างแบบแบ่งชั้น เรารับประกันว่ามีองค์ประกอบอย่างน้อยหนึ่งรายการจากแต่ละชั้นรวมอยู่ในตัวอย่าง	จำเป็นต้องทราบสัดส่วนของแต่ละชั้นจึงจะสามารถสุ่มตัวอย่างได้

ลักษณะสำคัญของการสุ่มตัวอย่างแบบแบ่งชั้นคือใช้ในการวิเคราะห์ทางสถิติแต่ละกลุ่มหรือชั้นที่มีการแบ่งประชากร แน่นอนว่า ประชากรทั้งหมดสามารถศึกษาได้ด้วยการสุ่มตัวอย่างประเภทนี้ นอกจากนี้ ประโยชน์ของการแบ่งชั้นข้อมูลจะมีมากขึ้นหากชั้นข้อมูลต่างกัน

ในทางตรงกันข้าม ข้อเท็จจริงของการแบ่งชั้นข้อมูลเพื่อให้สามารถดำเนินการสุ่มตัวอย่างได้นั้นหมายถึงความซับซ้อนของการสุ่มตัวอย่างที่เพิ่มขึ้น การสุ่มตัวอย่างแบบแบ่งชั้นมีความซับซ้อนในการดำเนินการมากกว่าเมื่อเปรียบเทียบกับการสุ่มตัวอย่างประเภทอื่น คุณสมบัตินี้ยังบอกเป็นนัยว่าเป็นตัวอย่างที่มีราคาแพงในการผลิต เนื่องจากต้องใช้เวลาในการแบ่งชั้นอย่างถูกต้อง

ข้อเสียอีกประการหนึ่งของการสุ่มตัวอย่างแบบแบ่งชั้นคือ ต้องใช้ข้อมูลจำนวนมากเกี่ยวกับประชากรที่ต้องการศึกษา ซึ่งไม่จำเป็นในการสุ่มตัวอย่างประเภทอื่นๆ เช่น การสุ่มตัวอย่างแบบธรรมดา แม้ว่าข้อเสียนี้สามารถบรรเทาลงได้หากผู้วิจัยมีความรู้ในสาขานี้เป็นอย่างดี

สุดท้ายนี้ ด้วยการสุ่มตัวอย่างแบบแบ่งชั้น เราจะได้ตัวอย่างที่เป็นตัวแทนของประชากรมากกว่าการสุ่มตัวอย่างประเภทอื่นๆ เพราะเรารับประกันว่าองค์ประกอบจากแต่ละชั้นจะรวมอยู่ด้วย ในทางตรงกันข้าม ในตัวอย่างนี้ ตัวอย่างที่ได้อาจไม่ประกอบด้วยองค์ประกอบใดๆ จากชั้นใดๆ

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การสุ่มตัวอย่างแบบแบ่งชั้นคืออะไร?

วิธีการสุ่มตัวอย่างแบบแบ่งชั้น

ประเภทของการสุ่มตัวอย่างแบบแบ่งชั้น

การสุ่มตัวอย่างแบบแบ่งชั้นตามสัดส่วน

การสุ่มตัวอย่างแบบแบ่งชั้นสม่ำเสมอ

การสุ่มตัวอย่างแบบแบ่งชั้นที่เหมาะสมที่สุด

ข้อดีและข้อเสียของการสุ่มตัวอย่างแบบแบ่งชั้น

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น