วิธีสร้างช่วงความเชื่อมั่นโดยใช้การแจกแจงแบบ f

เพื่อตรวจสอบว่าความแปรปรวนของประชากรทั้งสองเท่ากันหรือไม่ เราสามารถคำนวณอัตราส่วนความแปรปรวน σ ² ₁ / σ ² ₂ โดยที่ σ ² ₁ คือความแปรปรวนของประชากร 1 และ σ ² ₂ คือความแปรปรวนของประชากร 2

เพื่อประมาณอัตราส่วนความแปรปรวนของประชากรที่แท้จริง โดยทั่วไปเราจะ สุ่มตัวอย่างง่ายๆ จากประชากรแต่ละกลุ่มแล้วคำนวณอัตราส่วนความแปรปรวนตัวอย่าง s ₁ ² / s ₂ ² โดยที่ s ₁ ² และ s ₂ ² คือความแปรปรวนตัวอย่างสำหรับตัวอย่างที่ 1 และตัวอย่าง . 2 ตามลำดับ

การทดสอบนี้ถือว่า s ₁ ² และ s ₂ ² คำนวณจากตัวอย่างอิสระขนาด n ₁ และ n ₂ จากประชากรที่กระจายตามปกติ

ยิ่งอัตราส่วนนี้มาจากอัตราส่วนหนึ่งมากเท่าใด หลักฐานของความแปรปรวนที่ไม่เท่ากันภายในประชากรก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

ช่วงความมั่นใจ (1-α)100% สำหรับ σ ² ₁ / σ ² ₂ ถูกกำหนดเป็น:

(ส ₁ ² / วิ ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / วิ ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

โดยที่ F _{n 2 -1, n 1 -1, α/2} และ F _{n 1 -1, n 2 -1, α/2}   คือค่าวิกฤตของการแจกแจง F สำหรับระดับนัยสำคัญ α ที่เลือก

ตัวอย่างต่อไปนี้แสดงวิธีสร้างช่วงความมั่นใจสำหรับ σ ² ₁ / σ ² ₂ โดยใช้วิธีที่แตกต่างกัน 3 วิธี:

• ด้วยมือ
• ใช้ไมโครซอฟต์เอ็กเซล
• การใช้ซอฟต์แวร์สถิติ R

สำหรับแต่ละตัวอย่างต่อไปนี้ เราจะใช้ข้อมูลต่อไปนี้:

• α = 0.05
• ไม่มี ₁ = 16
• _n2 = 11
• ส ₁ ² =28.2
• ส ₂ ² = 19.3

การสร้างช่วงความมั่นใจด้วยตนเอง

ในการคำนวณช่วงความมั่นใจด้วยตนเองสำหรับ σ ² ₁ / σ ² ₂ เราจะแทนตัวเลขที่เรามีลงในสูตรช่วงความมั่นใจ:

(ส ₁ ² / วินาที ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / วินาที ₂ ² ) * F _{n2-1, n1-1, α/2}

ตัวเลขเดียวที่เราขาดหายไปคือค่าวิกฤต โชคดีที่เราสามารถค้นหาค่าวิกฤตเหล่านี้ได้ใน ตารางการแจกแจง F :

F _{n2-1, n1-1, α/2} = F _{10, 15, 0.025} = 3.0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0.025} = 1 / 3.5217 = 0.2839

(คลิกเพื่อขยายตาราง)

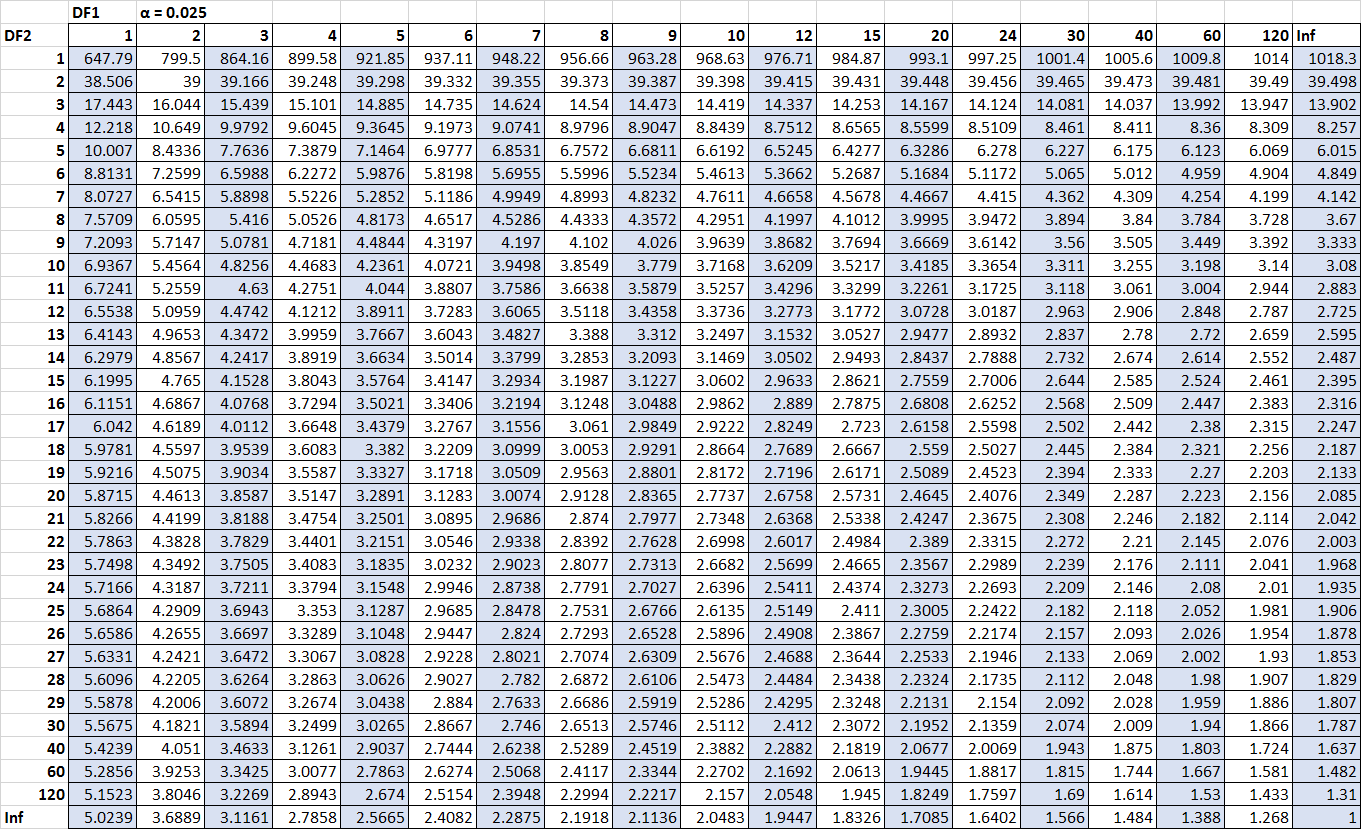
ตอนนี้เราสามารถแทนตัวเลขทั้งหมดลงในช่วงสูตรความมั่นใจได้แล้ว:

(ส ₁ ² / วินาที ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / วินาที ₂ ² ) * F _{n2-1, n1-1, α/2}

(28.2 / 19.3) * (0.2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28.2 / 19.3) * (3.0602)

0.4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4.4714

ดังนั้น ช่วงความเชื่อมั่น 95% สำหรับอัตราส่วนของความแปรปรวนประชากรคือ (0.4148, 4.4714)

การสร้างช่วงความเชื่อมั่นโดยใช้ Excel

รูปภาพต่อไปนี้แสดงวิธีการคำนวณช่วงความเชื่อมั่น 95% สำหรับอัตราส่วนผลต่างประชากรใน Excel ขีดจำกัดล่างและบนของช่วงความเชื่อมั่นจะแสดงในคอลัมน์ E และสูตรที่ใช้ค้นหาขีดจำกัดล่างและบนจะแสดงในคอลัมน์ F:

ดังนั้น ช่วงความเชื่อมั่น 95% สำหรับอัตราส่วนของความแปรปรวนประชากรคือ (0.4148, 4.4714) ซึ่งตรงกับสิ่งที่เราได้รับเมื่อเราคำนวณช่วงความเชื่อมั่นด้วยตนเอง

การสร้างช่วงความเชื่อมั่นโดยใช้ R

รหัสต่อไปนี้แสดงวิธีคำนวณช่วงความเชื่อมั่น 95% สำหรับอัตราส่วนของความแปรปรวนของประชากรใน R:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

ดังนั้น ช่วงความเชื่อมั่น 95% สำหรับอัตราส่วนของความแปรปรวนประชากรคือ (0.4148, 4.4714) ซึ่งตรงกับสิ่งที่เราได้รับเมื่อเราคำนวณช่วงความเชื่อมั่นด้วยตนเอง

แหล่งข้อมูลเพิ่มเติม

วิธีอ่านบอร์ดกระจาย F
วิธีค้นหาค่าวิกฤต F ใน Excel