Socs: ตัวย่อที่มีประโยชน์ในการอธิบายการแจกแจง

ในทางสถิติ เรามักต้องการทำความเข้าใจว่าชุดข้อมูลมีการกระจายอย่างไร โดยเฉพาะอย่างยิ่ง มีสี่สิ่งที่ควรรู้เกี่ยวกับการแจกแจง:

1 . รูปร่าง

• การกระจายสมมาตรหรือเบ้ไปด้านใดด้านหนึ่ง?
• การกระจายเป็นแบบยูนิโมดัล (หนึ่งพีค) หรือ ไบโมดัล (สองพีค) หรือไม่?

2. ค่าผิดปกติ

• มีค่าผิดปกติในการแจกแจงหรือไม่?

3. ศูนย์

• ค่าเฉลี่ย ค่ามัธยฐาน และรูปแบบการกระจายคืออะไร?

4.การแพร่กระจาย

• พิสัย พิสัยระหว่างควอร์ไทล์ ค่าเบี่ยงเบนมาตรฐาน และความแปรปรวนของการแจกแจงคือเท่าใด

SOCS เป็นตัวย่อที่มีประโยชน์ซึ่งเราสามารถใช้เพื่อจดจำสี่สิ่งนี้ แปลว่า “รูปร่าง, ค่าผิดปกติ, ศูนย์กลาง, การแพร่กระจาย”

มาดูตัวอย่างง่ายๆ ของวิธีใช้ SOCS เพื่ออธิบายการแจกแจงกัน

ตัวอย่าง: วิธีใช้ SOCS เพื่ออธิบายการแจกแจง

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงความสูงของตัวอย่างของพืช 20 ชนิดที่แตกต่างกัน

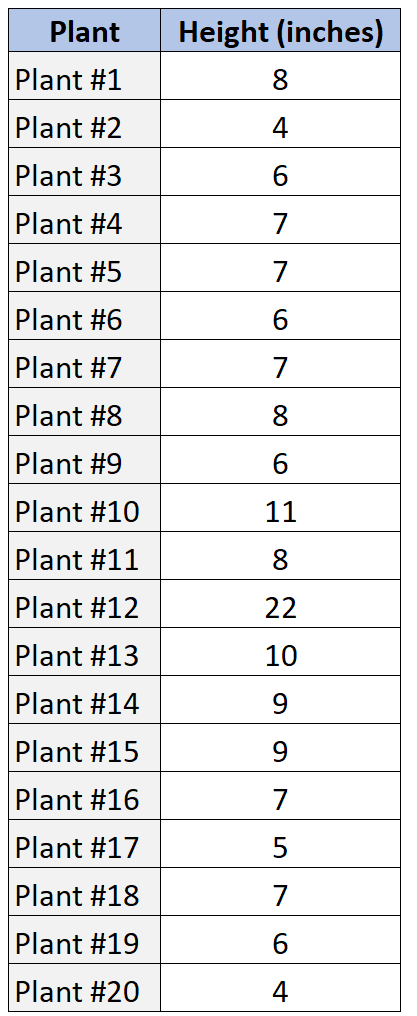
ต่อไปนี้คือวิธีที่เราสามารถใช้ SOCS เพื่ออธิบายการกระจายค่าข้อมูลนี้

รูปร่าง

อันดับแรก เราต้องการอธิบายรูปร่างของการกระจายตัว

วิธีที่เป็นประโยชน์ในการแสดงภาพรูปร่างของการแจกแจงคือการสร้างฮิสโตแกรม ซึ่งแสดงความถี่ของแต่ละค่าในชุดข้อมูล:

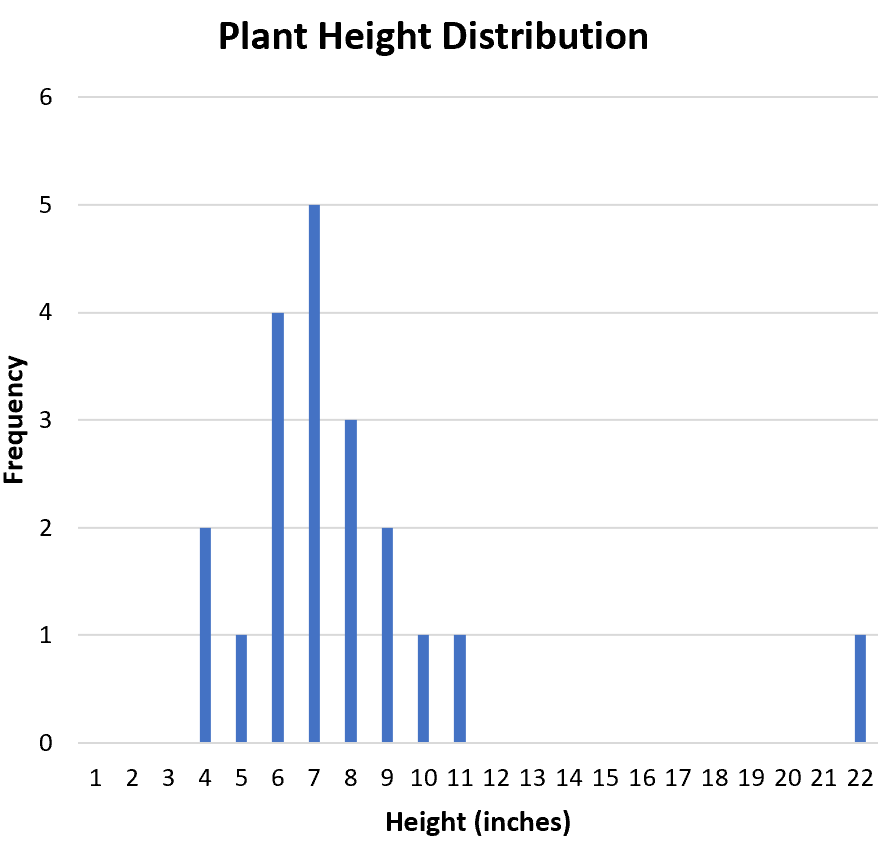
การกระจายสมมาตรหรือเบ้ไปด้านใดด้านหนึ่ง?   จากฮิสโตแกรมเราจะเห็นว่าการกระจายตัวมีความสมมาตรโดยประมาณ กล่าวอีกนัยหนึ่งค่านิยมจะไม่ลำเอียงไม่ทางใดก็ทางหนึ่ง

การกระจายเป็นแบบยูนิโมดัล (หนึ่งพีค) หรือไบโมดัล (สองพีค) หรือไม่? การกระจายเป็นแบบยูนิโมด มียอดอยู่ที่ค่า “7”

ค่าผิดปกติ

ต่อไป เราต้องการตรวจสอบว่ามีค่าผิดปกติในชุดข้อมูลหรือไม่ จากฮิสโตแกรม เราสามารถตรวจสอบการแจกแจงด้วยสายตาและเห็นว่า 22 อาจเป็นค่าผิดปกติ:

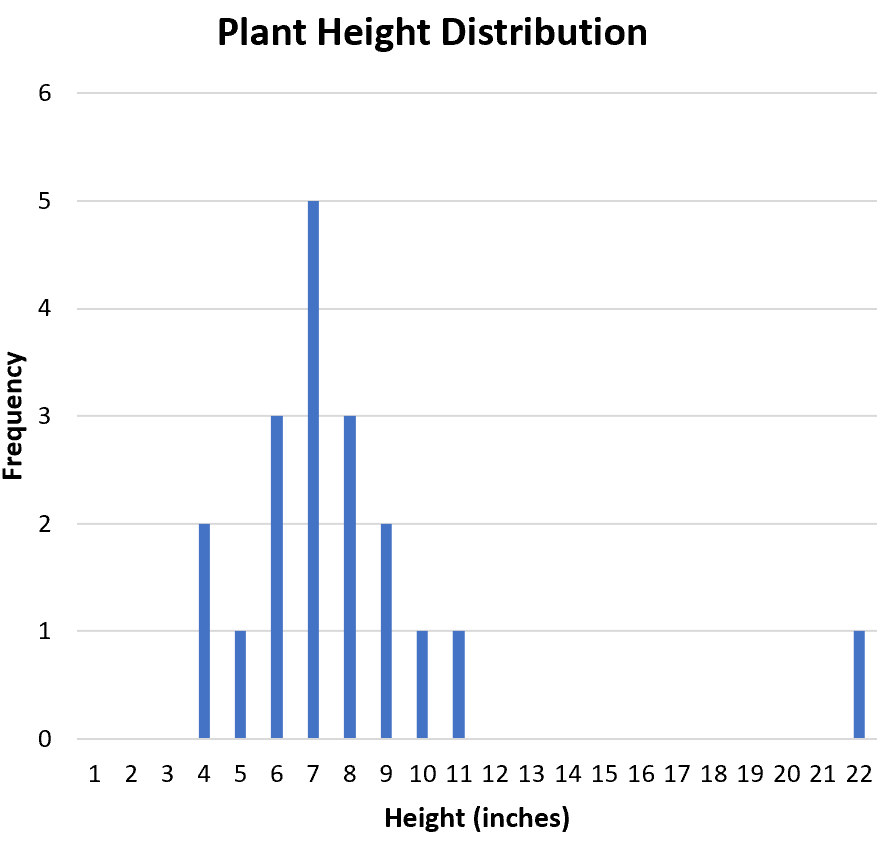
วิธีทั่วไปในการกำหนดค่าผิดปกติอย่างเป็นทางการคือค่าใดๆ ที่เป็น 1.5 เท่าของช่วงระหว่างควอไทล์ที่อยู่เหนือควอไทล์ที่ 3 หรือต่ำกว่าควอไทล์ที่ 1

เมื่อใช้เครื่องคำนวณช่วงระหว่างควอไทล์ เราสามารถป้อนค่าข้อมูลดิบ 20 ค่าและดูว่าควอไทล์ที่สามคือ 9 ช่วงระหว่างควอไทล์คือ 3 ดังนั้นค่าใดๆ ที่มากกว่า 9 + (1.5*3) = 13.5 ถือเป็นค่าผิดปกติ ตามคำนิยาม

เนื่องจาก 22 มากกว่า 13.5 เราจึงสามารถประกาศให้ 22 มีค่าผิดปกติได้

ศูนย์

จากนั้นเราต้องการอธิบายว่าศูนย์กลางการกระจายอยู่ที่ใด ตัวชี้วัดทั่วไปสามประการของแนวโน้มจากศูนย์กลาง ที่เราสามารถใช้ได้คือค่าเฉลี่ย ค่ามัธยฐาน และโหมด

ค่าเฉลี่ย: นี่คือค่าเฉลี่ยของการแจกแจง เราพบสิ่งนี้โดยการบวกค่าแต่ละค่าทั้งหมดแล้วหารด้วยจำนวนค่าทั้งหมด:

ค่าเฉลี่ย = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7.85

ค่ามัธยฐาน: นี่คือค่า “เฉลี่ย” ของการแจกแจง เราพบสิ่งนี้โดยการเรียงลำดับค่าทั้งหมดจากน้อยไปมากแล้วระบุค่ามัธยฐาน กลายเป็น 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

โหมด: นี่คือค่าที่ปรากฏบ่อยที่สุด กลายเป็น 7 .

การแพร่กระจาย

ต่อไป เราต้องการอธิบายการกระจายตัวของค่าในการแจกแจง การวัดการกระจายทั่วไปสี่ประการที่เราสามารถใช้ได้คือ พิสัย พิสัยระหว่างควอไรล์ ค่าเบี่ยงเบนมาตรฐาน และความแปรปรวน

ช่วง: นี่คือความแตกต่างระหว่างค่าที่ใหญ่ที่สุดและน้อยที่สุดในชุดข้อมูล นี่กลายเป็น 22 – 4 = 18

ช่วงระหว่างควอไทล์: วัดความกว้างตรงกลาง 50% ของค่าข้อมูล เมื่อป้อนข้อมูลดิบ 20 ค่าลงในเครื่องคำนวณช่วงระหว่างควอไทล์ เราจะเห็นว่ามีค่าเท่ากับ 3

ส่วนเบี่ยงเบนมาตรฐาน: นี่คือการวัดการกระจายตัวของค่าข้อมูลโดยเฉลี่ย เมื่อป้อนข้อมูลดิบ 20 ค่าลงในเครื่องคำนวณความแปรปรวนและค่าเบี่ยงเบนมาตรฐาน เราจะเห็นว่าค่าเบี่ยงเบนมาตรฐานเท่ากับ 3.69

ความแปรปรวน: นี่เป็นเพียงค่าเบี่ยงเบนมาตรฐาน กำลังสอง ซึ่งเท่ากับ 3.69 ² = 13.63

บทสรุป

การใช้ SOCS เป็นแนวทาง เราสามารถอธิบายการกระจายความสูงของพืชได้ดังนี้

• การกระจายเป็นแบบยูนิโมดัลและสมมาตร หมายความว่ามียอดเพียงจุดเดียวและไม่เบ้ไปด้านใดด้านหนึ่ง
• การแจกแจงมีค่าผิดปกติหนึ่งค่า: 22
• การแจกแจงมีค่าเฉลี่ย 7.85 มัธยฐาน 7 และโหมด 7
• การแจกแจงมีช่วง 18 ช่วงระหว่างควอไทล์อยู่ที่ 3 ค่าเบี่ยงเบนมาตรฐาน 3.69 และความแปรปรวน 13.63

โปรดทราบว่าเราสามารถใช้ SOCS เพื่ออธิบายการแจกแจงใดๆ ซึ่งเป็นวิธีที่มีประโยชน์สำหรับเราในการทำความเข้าใจรูปร่างของการแจกแจงอย่างถ่องแท้ ไม่ว่าจะมีค่าผิดปกติ โดยที่จุดศูนย์กลางอยู่ที่ประมาณ และวิธีการกระจายค่าข้อมูล เป็น.