วิธีทำการทดสอบฟรีดแมนใน stata
การทดสอบฟรีดแมน เป็นทางเลือกแบบไม่ใช้พารามิเตอร์ ในการวัดความแปรปรวนแบบซ้ำๆ ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มสามกลุ่มขึ้นไปซึ่งมีวิชาเดียวกันปรากฏในแต่ละกลุ่มหรือไม่
บทช่วยสอนนี้จะอธิบายวิธีดำเนินการทดสอบฟรีดแมนใน Stata
ตัวอย่าง: การทดสอบฟรีดแมนใน Stata
สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล t43 ซึ่งแสดงเวลาตอบสนองของผู้ป่วย 5 รายที่รับประทานยาที่แตกต่างกัน 4 ชนิด เนื่องจากผู้ป่วยแต่ละรายจะถูกวัดด้วยยาแต่ละชนิดจากทั้งหมดสี่ชนิด เราจะใช้การทดสอบของฟรีดแมนเพื่อพิจารณาว่าเวลาตอบสนองโดยเฉลี่ยแตกต่างกันระหว่างยาแต่ละชนิดหรือไม่
ทำตามขั้นตอนต่อไปนี้เพื่อทำการทดสอบฟรีดแมน:
ขั้นตอนที่ 1: โหลดและแสดงข้อมูล
ใช้คำสั่งต่อไปนี้เพื่อโหลดข้อมูลลงใน Stata:
ใช้ https://www.stata-press.com/data/r14/t43
ดูข้อมูลดิบโดยใช้คำสั่งต่อไปนี้:
พี่ชาย
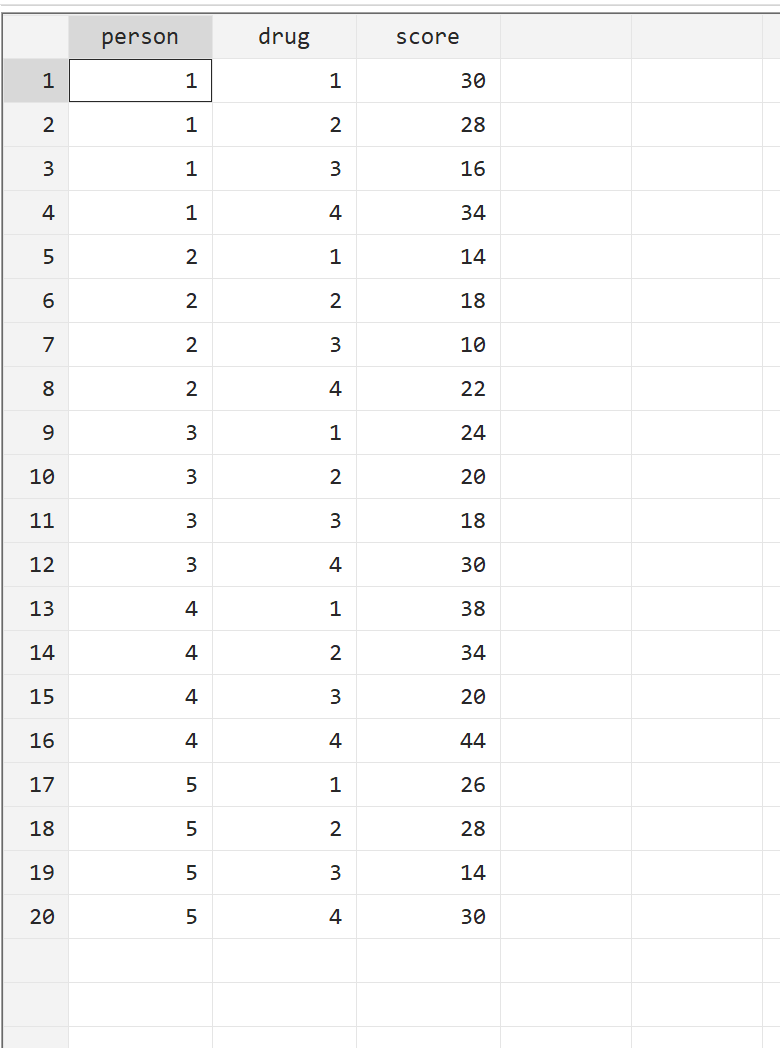
ขั้นตอนที่ 2: ติดตั้งแพ็คเกจ emh
ในการทำการทดสอบฟรีดแมน เราจะต้องติดตั้งแพ็คเกจ emh ซึ่งไม่ได้ติดตั้งไว้ล่วงหน้าใน Stata หากต้องการติดตั้ง เพียงพิมพ์คำสั่งต่อไปนี้:
ssc ติดตั้ง emh
ควรติดตั้งโดยอัตโนมัติภายในไม่กี่วินาที
ขั้นตอนที่ 3: ทำการทดสอบฟรีดแมน
เมื่อติดตั้งแพ็คเกจ emh แล้ว เราจะสามารถทำการทดสอบฟรีดแมนได้โดยใช้ไวยากรณ์ต่อไปนี้:
ตัวแปรการตอบสนอง emh explanatory_variable, ชั้น (ตัวแปรซ้ำ) การแปลง anova (อันดับ)
ในกรณีของเรา เราจะใช้ไวยากรณ์ต่อไปนี้:
คะแนนยา emh ชั้น (คน) การเปลี่ยนแปลงของ anova (อันดับ)

ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:
ค(3) = 13.5600. นี่คือสถิติการทดสอบของฟรีดแมน
ป = 0.0036 . นี่คือค่า p ที่เกี่ยวข้องกับสถิติการทดสอบ เนื่องจากค่านี้น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างที่ว่าเวลาตอบสนองโดยเฉลี่ยเท่ากันสำหรับยาทั้งสี่ชนิด เรามีหลักฐานเพียงพอที่จะสรุปว่าประเภทของยาที่ใช้ส่งผลให้เกิดความแตกต่างที่มีนัยสำคัญทางสถิติในเวลาตอบสนอง
ขั้นตอนที่ 4: รายงานผลลัพธ์
สุดท้ายนี้เราอยากจะรายงานผลการทดสอบ นี่คือตัวอย่างของวิธีการทำเช่นนี้:
ทำการทดสอบฟรีดแมนกับคน 5 คนเพื่อตรวจสอบผลของยาสี่ชนิดที่แตกต่างกันตามเวลาตอบสนอง แต่ละคนใช้ยากันคนละครั้ง
ผลการศึกษาพบว่าประเภทของยาที่ใช้ส่งผลให้เวลาตอบสนองแตกต่างกันอย่างมีนัยสำคัญทางสถิติ (Q(3) = 13.56, p = 0.0036)