วิธีสร้างและตีความเส้นโค้ง roc ใน stata

การถดถอยแบบลอจิสติก เป็นวิธีการทางสถิติที่เราใช้เพื่อปรับให้เหมาะสมกับแบบจำลองการถดถอยเมื่อตัวแปรตอบสนองเป็นไบนารี เพื่อประเมินว่าแบบจำลองการถดถอยโลจิสติกเหมาะสมกับชุดข้อมูลได้ดีเพียงใด เราสามารถดูตัวชี้วัดสองตัวต่อไปนี้:

• ความไว: ความน่าจะเป็นที่แบบจำลองคาดการณ์ผลลัพธ์ที่เป็นบวกสำหรับการสังเกต เมื่อผลลัพธ์เป็นบวกจริงๆ
• ความจำเพาะ: ความน่าจะเป็นที่แบบจำลองทำนายผลลัพธ์ที่เป็นลบสำหรับการสังเกต เมื่อผลลัพธ์เป็นลบจริงๆ

วิธีง่ายๆ ในการแสดงภาพเมตริกทั้งสองนี้คือการสร้าง เส้นโค้ง ROC ซึ่งเป็นกราฟที่แสดงความไวและความเฉพาะเจาะจงของแบบจำลองการถดถอยลอจิสติก

บทช่วยสอนนี้จะอธิบายวิธีสร้างและตีความเส้นโค้ง ROC ใน Stata

ตัวอย่าง: เส้นโค้ง ROC ใน Stata

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูลชื่อ lbw ซึ่งมีตัวแปรต่อไปนี้สำหรับมารดา 189 คน:

• ต่ำ – ทารกมีน้ำหนักแรกเกิดน้อยหรือไม่ 1 = ใช่ 0 = ไม่ใช่
• อายุ – อายุของแม่
• สูบบุหรี่ – ไม่ว่าแม่จะสูบบุหรี่ในระหว่างตั้งครรภ์หรือไม่ก็ตาม 1 = ใช่ 0 = ไม่ใช่

เราจะใส่แบบจำลองการถดถอยโลจิสติกเข้ากับข้อมูลโดยใช้อายุและการสูบบุหรี่เป็นตัวแปรอธิบาย และน้ำหนักแรกเกิดต่ำเป็นตัวแปรตอบสนอง ต่อไป เราจะสร้างเส้นโค้ง ROC เพื่อวิเคราะห์ว่าแบบจำลองเหมาะสมกับข้อมูลเพียงใด

ขั้นตอนที่ 1: โหลดและแสดงข้อมูล

โหลดข้อมูลโดยใช้คำสั่งต่อไปนี้:

ใช้ https://www.stata-press.com/data/r13/lbw

ทำความเข้าใจชุดข้อมูลอย่างรวดเร็วโดยใช้คำสั่งต่อไปนี้:

เพื่อสรุป

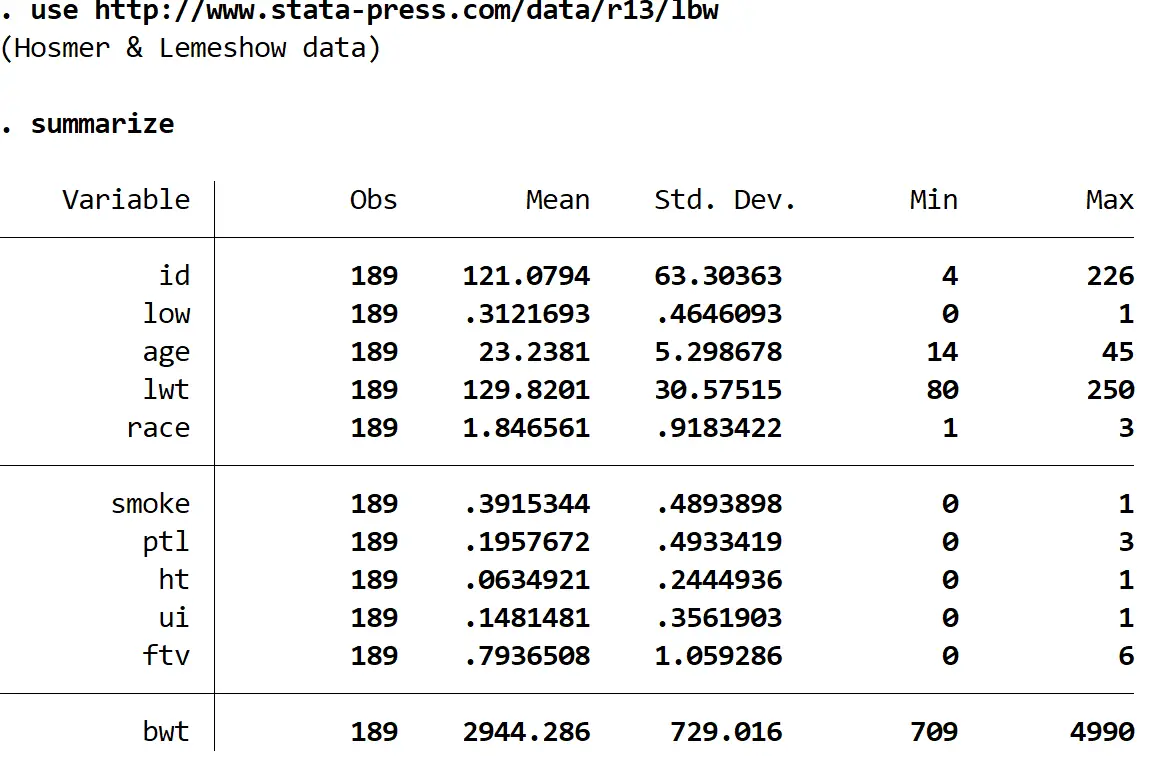
ชุดข้อมูลมีตัวแปรที่แตกต่างกัน 11 ตัว แต่ตัวแปรเพียงสามตัวที่เราสนใจคือระดับต่ำ อายุ และการสูบบุหรี่

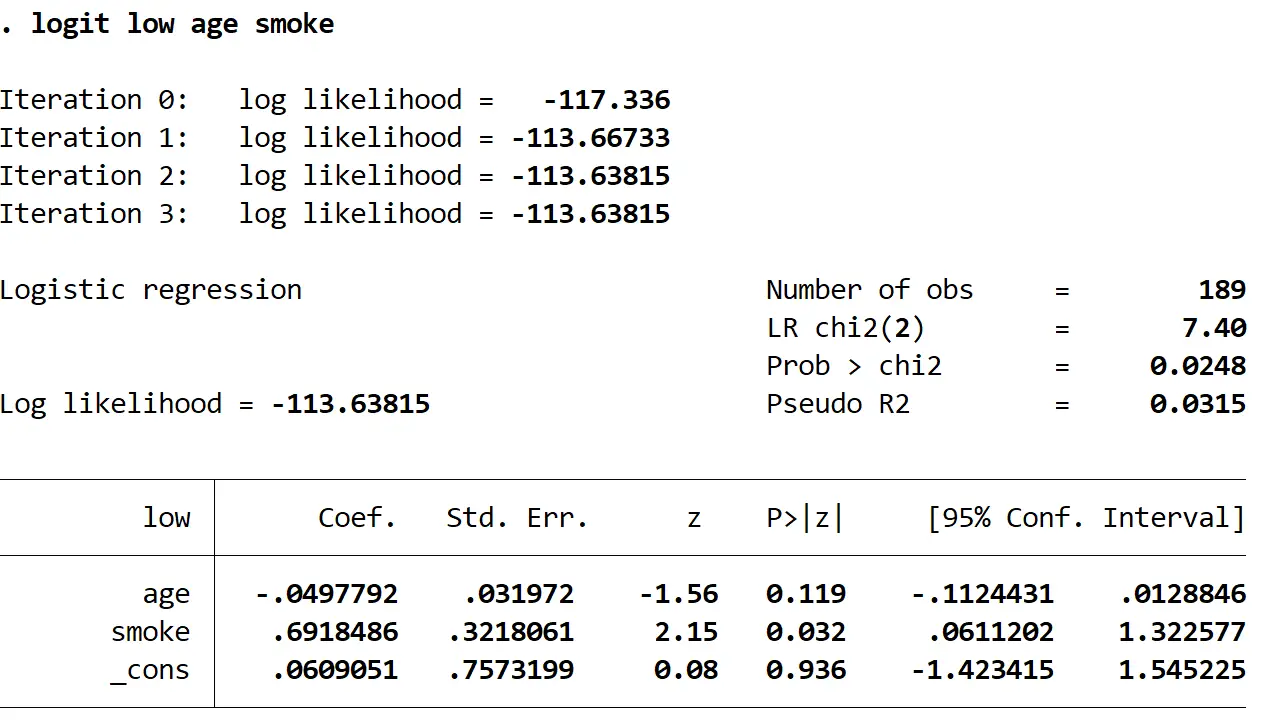
ขั้นตอนที่ 2: ติดตั้งแบบจำลองการถดถอยโลจิสติก

ใช้คำสั่งต่อไปนี้เพื่อให้เหมาะสมกับแบบจำลองการถดถอยโลจิสติก:

บันทึกควันอายุต่ำ

ขั้นตอนที่ 3: สร้างเส้นโค้ง ROC

เราสามารถสร้างเส้นโค้ง ROC สำหรับโมเดลโดยใช้คำสั่งต่อไปนี้:

ล็อค

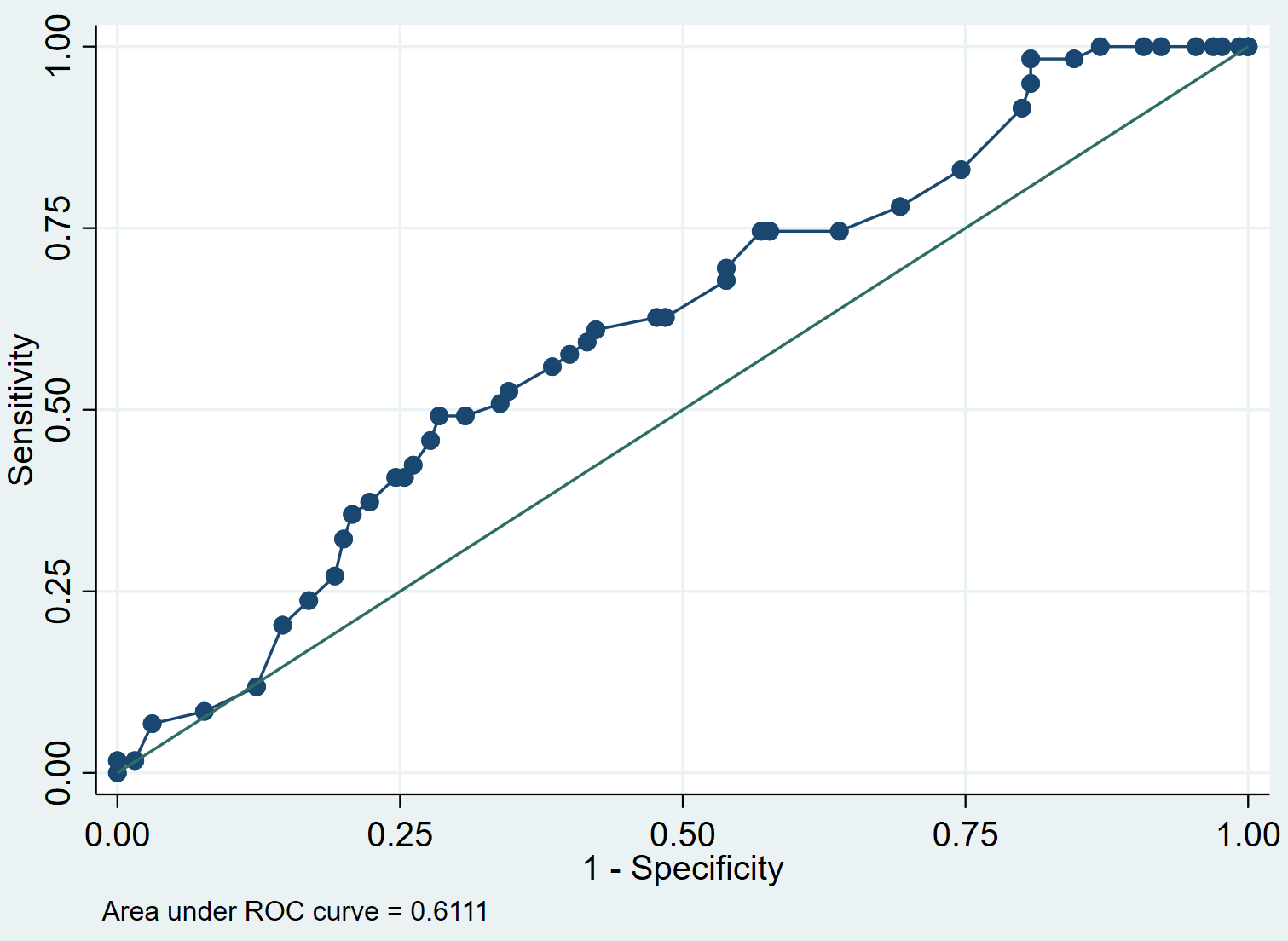
ขั้นตอนที่ 4: ตีความเส้นโค้ง ROC

เมื่อเราพอดีกับแบบจำลองการถดถอยโลจิสติก ก็สามารถใช้เพื่อคำนวณความน่าจะเป็นที่การสังเกตที่กำหนดจะมีผลในเชิงบวก โดยขึ้นอยู่กับค่าของตัวแปรทำนาย

ในการพิจารณาว่าการสังเกตควรจัดประเภทเป็นบวกหรือไม่ เราสามารถเลือกเกณฑ์ เช่น การสังเกตที่มีความน่าจะเป็นที่ปรับแล้วเหนือเกณฑ์นั้นจะถูกจัดประเภทเป็นบวก และการสังเกตทั้งหมดที่มีความน่าจะเป็นที่ปรับแล้วต่ำกว่าเกณฑ์นั้นจะถูกจัดประเภทเป็นลบ .

ตัวอย่างเช่น สมมติว่าเราเลือกเกณฑ์ที่ 0.5 ซึ่งหมายความว่า การสังเกตใดๆ ที่มีความน่าจะเป็นที่ปรับแล้วน้อยกว่า 0.5 จะมีผลเป็นบวก ในขณะที่การสังเกตใดๆ ที่มีความน่าจะเป็นที่ปรับแล้วน้อยกว่าหรือเท่ากับ 0.5 จะมีผลเป็นลบ

เส้นโค้ง ROC แสดงให้เราเห็นค่าความไวเทียบกับความจำเพาะ 1 เนื่องจากค่าเกณฑ์เปลี่ยนจาก 0 เป็น 1 โมเดลที่มีความไวและความจำเพาะสูงจะมีเส้นโค้ง ROC ที่โอบมุมซ้ายบนของโครงเรื่อง แบบจำลองที่มีความไวต่ำและความจำเพาะต่ำจะมีเส้นโค้งใกล้กับเส้นทแยงมุม 45 องศา

AUC (พื้นที่ใต้เส้นโค้ง) ช่วยให้เราเข้าใจถึงความสามารถของแบบจำลองในการแยกแยะระหว่างผลลัพธ์เชิงบวกและเชิงลบ AUC สามารถอยู่ในช่วงตั้งแต่ 0 ถึง 1 ยิ่ง AUC สูงเท่าใด โมเดลก็จะยิ่งจำแนกผลลัพธ์ได้อย่างถูกต้องมากขึ้นเท่านั้น ในตัวอย่างของเรา เราจะเห็นว่า AUC คือ 0.6111

เราสามารถใช้ AUC เพื่อเปรียบเทียบประสิทธิภาพของรุ่นตั้งแต่สองรุ่นขึ้นไป โมเดลที่มี AUC สูงสุดจะทำงานได้ดีที่สุด

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยโลจิสติกใน Stata
วิธีการตีความเส้นโค้ง ROC และ AUC ของแบบจำลองการถดถอยโลจิสติก